37. Расстояние а) от точки до прямой,

Дано: , l : , М₁(x₁, y₁, z₁).

Найти расстояние d (M₁, l).

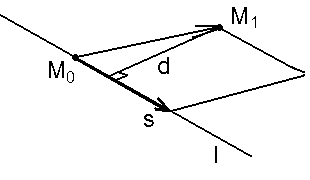
Из уравнений прямой l следует, что точка M₀ (x₀, y₀, z₀ ) лежит на прямой l и вектор параллелен этой прямой. Искомое расстояние равно высоте параллелограмма, построенного на векторах и как на сторонах (рис. 37). Следовательно,

.Переписав это равенство в координатах, получим (53)

б) между скрещивающимися прямыми.

Дано: , l₁ : ,l₂ : , l₁ и l₂ скрещиваются.

Найти d (l₁, l₂).

Из уравнений l₁ и l₂ следует, что M₁ (x₁, y₁, z₁)  l₁,M₂ (x₂, y₂, z₂) l₂ и векторы и параллельны прямым l₁ и l₂ соответственно. Искомое расстояние равно высоте параллелепипеда, построенного на векторах , и .

Следовательно, .Переписав это равенство в координатах, получим

(54)

Задача 19. Дано: , l₁ : l₂ :

Проверьте, что l₁ и l₂ скрещиваются и найдите расстояние между ними.

Решение. Найдём направляющий вектор прямой l₁ и какую-нибудь точку на ней.

, М₁ = {1, 2, 9}. Из уравнений l₂ следует, что

М₂ (4, 1, 0) и 1, 3}. Вычислим 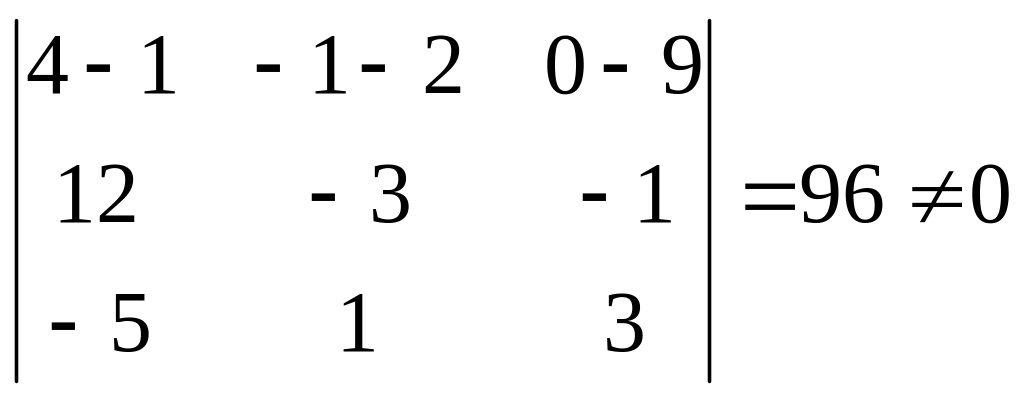. Следовательно, l₁ и l₂ скрещиваются. Найдём . Следовательно, = и .

38. Угол между а) двумя прямыми,

б) прямой и плоскостью.

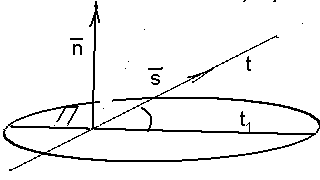
Дано: , П : Ах + Ву + Сz + D = 0, t : .

Найти один из углов между П и t.

Решение. Угол между прямой и плоскостью – это угол между прямой и её ортогональной проекцией на плоскость . Из уравнений прямой и плоскости вектор перпендикулярен плоскости П, а вектор параллелен прямой t . Следовательно, ). Отсюда следует, что sin(П, = (50)

Из свойств векторов и следует: П  t  ; П  t  (51)

а)Угол между двумя прямыми в пространстве

За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.

Один из этих углов равен углу между направляющими векторами этих прямых.

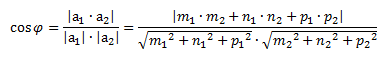
Где первая прямая задается:

а₁=(m_1,n₁,p₁)

Вторая прямая задается:

а₂=( m₂, n₂, p₂)

Если прямые параллельны, то

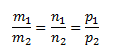
Если прямые перпендикулярны, то m₁m₂+n₁n₂+p₁p₂=0.

39. Геометрический смысл неравенств Ах + Ву + Сz + D  0 (< 0, > 0,  0).

Дано: R = , Ах + Ву + Сz + D  0.

Исследовать, какую фигуру задаёт данное неравенство.

Уравнение Ах + Ву + Сz + D = 0 задаёт плоскость. Пусть это плоскость П. Рассмотрим все точки пространства, не лежащие на П.

Вектор не параллелен плоскости П. Действительно, если бы был параллелен П, то АА + ВВ + СС = А² + В² + С²= 0. Но это не возможно. Рассмотрим множество всех точек пространства, не лежащих на плоскости П. Пусть М – любая из этих точек. Проведём через точку М прямую, параллельную вектору , и пусть она пересекает П в точке N. Векторы и коллинеарны, , следовательно, . () Очевидно,   0  когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор . И   0  когда точки М лежат в другой открытой полуплоскости с этой же границей. Перейдём к координатам. Пусть М (х, у, z) и N (х₁, у₁, z₁). Тогда = {x  x₁, y  y₁, z  z₁}. Равенство () в координатах перепишется:x  x₁ = A, y  y₁ = B, z  z₁ = C.

Отсюда x₁ = x  A, y₁ = y  B, z₁ = z  C. Так как N  П, то Ах₁ + Ву₁ + Сz₁ + D = 0. Следовательно, А(x  A) + В(y  B) + С (z  C) + D = 0. Ах + Ву + Сz + D =  (A² + B² + C²).

Так как A² + B² + C²  0, то знак Ах + Ву + Сz + D совпадает со знаком .

Итак, Ах + Ву + Сz + D  0  точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор . Ах + Ву + Сz + D  0  точки М лежат в другой открытой полуплоскости с этой же границей.

Неравенства Ах + Ву + Сz + D  0 и Ах + Ву + Сz + D  0 определяют замкнутые полуплоскости (их называют просто полуплоскости) с границей П.

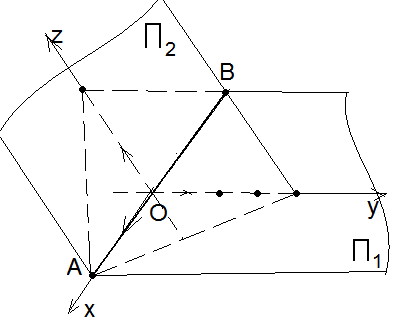
Задача 20. Какую фигуру задаёт в аффинной системе координат система ? Решение. Уравнение x + z  2 = 0 задаёт плоскость П₁, параллельную оси (Оу) и пересекающую оси (Ох) и (Оz) в точках (2, 0, 0) и (0, 0, 2) соответственно. Неравенство задаёт полуплоскость с границей П₁, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y  4 = 0 определяет плоскость П₂, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство задаёт полуплоскость с границей П₂ , в которой не лежит начало координат. Плоскости П₁ и П₂ пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П₁ и П₂, ни в одном из которых не лежит начало координат.