LIi. Плоскость и прямая в пространстве

28. Уравнения плоскости, проходящей через

а )данную точку параллельно двум неколлинеарным векторам;

Дано: R = , М₀(х₀, у₀, z₀), , , и неколлинеарны; П  М₀ , П  , П  .

Найти условия, определяющие П (рис. 46).

Решение. М  П  , и компланарны. Так как и неколлинеарны, то М  П  либо ( u,v  любые действительные числа), либо определитель, составленный из координат этих векторов, равен нулю. Перепишем эти условия в координатах. Получим М  П  или М  П  (39)

Получили два вида уравнений плоскости: уравнение (39) и (40).

Уравнения (40) называются параметрическими уравнениями плоскости, проходящей через данную точку параллельно двум данным векторам.

Так как , где и  радиусы-векторы точек М и М₀ соответственно. Тогда уравнение можно переписать (41). Это векторное уравнение плоскости.

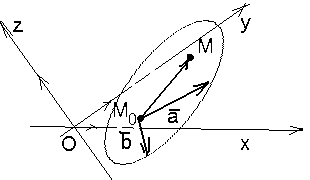
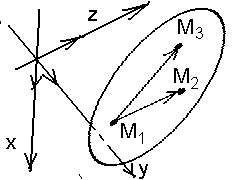
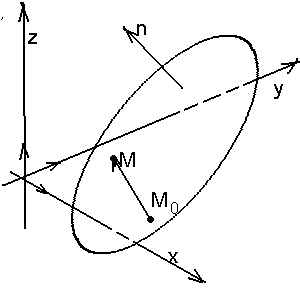
Рис. 46 Рис. 47 Рис. 48

б)три не лежащие на одной прямой точки;

Дано: R = , М₁(х₁, у₁,z₁), М₂(х₂, у₂, z₂), М₃(x₃, у₃, z₃), точки M₁, M₂, M₃ не коллинеарные. П   M₁, M₂, M₃.

Найти уравнения П (рис. 47).

Решение. Так как M₁, M₂, M₃ не коллинеарные, то векторы

и неколлинеарны. Используя уравнение (41), получим векторное уравнение плоскости, проходящей через три данные точки:

. (42)

Используя (40) и (39), получим параметрические уравнения плоскости П и её уравнение в форме определителя. (43); (44)

в)данную точку перпендикулярно данному вектору.

Дано: , М₀(х₀, у₀, z₀), , ,П  М₀, П  .

Найти уравнение П.

Решение. М  П  либо , либо  . Так как , то М  П  (47)Это векторное уравнение данной плоскости.

Переходя к координатам, получим А(х  х₀) + В(у  у₀) + С(z  z₀) = 0(48)

Можно показать, что если плоскость задана в ПДСК общим уравнением (45), то вектор перпендикулярен этой плоскости.

29. Общее уравнение плоскости.

Если в уравнениях (39) или (44) раскрыть определители, то получим уравнение первой степени с тремя переменными, следовательно, в аффинной системе координат всякая плоскость может быть задана некоторым уравнением вида Ах + Ву + Сz + D = 0. Поставим обратную задачу: всякое ли уравнение вида Ах + Ву + Сz + D = 0 задаёт в аффинной системе координат некоторую плоскость.

Дано: R = , Ах + Ву + Сz + D = 0 (45), где коэффициенты А, В, С не все равны нулю.

Доказать: уравнение (45) задаёт плоскость.

Доказательство. Проведём доказательство, предполагая, что А  0. Если y = z = 0, то . Следовательно, координаты точки М₀ ( , 0, 0) удовлетворяют уравнению (45), т.е. если плоскость существует, то она обязательно пройдёт через эту точку. Векторы и , очевидно, не коллинеарны. Используя (39), составим уравнение плоскости, проходящей через точку М₀ параллельно векторам и . Получим

После упрощения: Ах + Ву + Сz + D = 0, т.е. данное уравнение. Итак, (45) действительно задаёт плоскость.

Уравнение (45) называется общее уравнение плоскости.

Следствие. Если плоскость задана общим уравнением (45), то из векторов , и хотя бы два отличны от и неколлинеарны. Любой ненулевой вектор из них параллелен данной плоскости.

30. Нормальное уравнение плоскости. Приведение общего уравнения плоскости к нормальному виду.

где   - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.

Приведение общего уравнения плоскости к нормальному виду:

Здесь 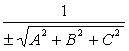- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если  произвольно, если D = 0.

31. Исследование взаимного расположения двух и трёх плоскостей.

Дано: R = , П₁ : А₁х + В₁у + С₁z + D₁ = 0, П₂ : А₂х + В₂у + С₂z + D₂ = 0.

Исследовать взаимное расположение П₁, П₂ .

Решение. Задача сводится к исследованию системы (46)

Возможны случаи.

1.А₁,В₁,С₁ и А₂, В₂, С₂ не пропорциональны. В этом случае система (46) имеет бесконечно много решений, но уравнения не пропорциональны. На геометрическом языке получаем, что плоскости имеют бесконечно много общих точек, но не совпадают. Следовательно, П₁ и П₂ пересекаются по прямой.

Замечание. Если прямая задана общими уравнениями (19), то каждое отдельно взятое уравнение задаёт прямую, т.е. прямая задаётся как линия пересечения двух плоскостей.

2. . В этом случае уравнения системы (46) эквивалентны, т.е. каждое решение одного из них является решением второго. На геометрическом языке: каждая точка одной плоскости лежит на другой, т.е. плоскости совпадают.

3. . В этом случае системы (46) не имеет решений. На геометрическом языке: плоскости не имеют общих точек.

Следствие. Плоскости П₁ : А₁х + В₁у + С₁z + D₁ = 0, П₂ : А₂х + В₂у + С₂z + D₂ = 0 параллельны тогда и только тогда, когда .

Задача 16. Исследовать взаимное расположение плоскостей, если одна из них задании общим уравнением, а вторая – параметрическими уравнениями.

Дано: R = , П₁ : Ах + Ву + Сz + D = 0, П₂ : Исследовать взаимное расположение П₁, П₂ .

Решение. Задача сводится к исследованию системы ()

Подставив выражения х, у, z в первое уравнение и преобразовав его, получим

()

Возможны случаи:

1)  0 ( или  0). В этом случае уравнение () имеет бесконечно много решений, зависящих от одного параметра. Следовательно, система () тоже имеет бесконечно много решений, зависящих от одного параметра. На геометрическом языке это значит, что плоскости пересекаются по прямой.

2) = 0, = 0, = 0. В этом случае уравнение () имеет вид 0u + 0v + 0 = 0. Этому уравнению удовлетворяют все возможные значения u и v. На геометрическом языке это значит, что все точки первой плоскости лежат на второй и наоборот. Следовательно, плоскости совпадают.

3) = 0, = 0,  0. В этом случае уравнение () имеет вид 0u + 0v + ( ) = 0. Это уравнение не имеет ни одного решения. На геометрическом языке это значит, что данные плоскости не имеют общих точек.

Следствие. Если П₁ : Ах + Ву + Сz + D = 0, П₂ : то П₁ || П₂  = 0, = 0.

32. Угол между двумя плоскостями. Условия перпендикулярности двух плоскостей.

Дано: , П₁ : А₁х + В₁у + С₁z + D₁ = 0, П₂ : А₂х + В₂у + С₂z + D₂ = 0.

Найти один из углов между П₁ и П₂ .

Решение. Из уравнений П₁ и П₂ следует, что и перпендикулярны плоскостям П₁ и П₂ соответственно. Если О – точка на линии пересечения П₁ и П₂, t₁ и t₂ лежат в плоскостях П₁ и П₂, проходят через точку О и перпендикулярны линии пересечения этих плоскостей (рис. 34), то = (П₁, П₂). Но по свойству углов со взаимно перпендикулярными сторонами либо равен углу , либо дополняет его до 180⁰. И в том, и в другом случае равен одному из углов между П₁ и П₂ . Следовательно,

Cos((П₁, П₂) = (49)

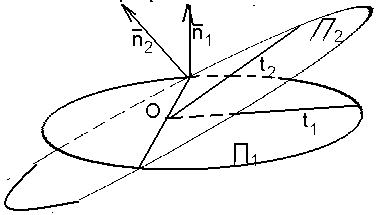
Рис. 49 Рис. 51

Условие перпендикулярности двух плоскостей

Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости.

или