23. Нормальное уравнение прямой. Приведение общего уравнения прямой к нормальному виду.

Дано: R = , : , , l  Р, l  .

Найти уравнение l.

М  l  пр = р. Отсюда М  l  . Так как , , то М  l  . Отсюда М  l  (30)

Уравнение (30) называется нормальное уравнение прямой. В этом уравнении

(cos)² + (sin)² = 1, свободный член (р)  0.

Очевидно, нормальное уравнение прямой является одним из общих её уравнений. Если прямая задана в аффинной системе координат уравнением Ax + By + C = 0, то все остальные её общие уравнения имеют вид Ax + By + C = 0, где   0 (). Следовательно, существует такое , при котором уравнение () будет нормальным уравнением данной прямой. Для этого должны выполняться условия (А)² + (В)² = 1, (С)  0. Отсюда и знак перед корнем должен быть противоположен знаку С. (Если С = 0, то знак можно взять любой). Коэффициент называется нормирующим множителем, а уравнение будет нормальным уравнением данной прямой. Говорят, что уравнение Ax + By + C = 0 приведено к нормальному виду.

24. Угол между прямыми, заданными а) общими уравнениями;

Дано: R = , l₁ : A₁x + B₁y + C₁ = 0, l₂ : A₂x + B₂y + C₂ = 0.

Найти один из углов .

Замечание. Очевидно, достаточно найти только один из углов между прямыми.

Решение: Первый способ. Из уравнений l₁ и l₂ следует, что вектор параллелен прямой l₁ и вектор параллелен прямой l₂. Следовательно, один из углов между l₁ и l₂ равен углу . Итак,

. (31)

(Вывод формулы (31) можно проводить в любой аффинной системе координат). Воспользовавшись тем, что данная система координат прямоугольная, перепишем формулу (31) в координатах. Получим . Окончательно получим

(32)

Рис 38 Рис. 39

Второй способ. Из уравнений l₁ и l₂ следует, что вектор перпендикулярен прямой l₁ и вектор перпендикулярен прямой l₂. Из свойства углов со взаимно перпендикулярными сторонами следует, что один из углов между l₁ и l₂ равен углу . Итак,

(33)

Переписав полученную формулу в координатах, получим

. (32)

Замечание. Формулу (32) можно использовать только в том случае, когда прямые заданы общими уравнениями в прямоугольной системе координат.

Следствие. Две прямые перпендикулярны тогда и только тогда, когда А₁А₂ + В₁В₂ = 0 (33).

Задача 12. Дано. R = , , , , l₁ : 3х  4у + 11 = 0,

l₂ : 5х + у + 8 = 0.

Найти .

Решение. Используем формулу (31). В нашем случае = , . Следовательно, ; , . Подставив в формулу (31), получим .

б) уравнениями с угловыми коэффициентами.

Дано: R = , l₁ : у = к₁ х + в₁, l₂ : у = к₂ х + в₂.

Найти ориентированный угол, на который нужно повернуть l₁, чтобы она стала параллельной l₂.

Решение. Из уравнений l₁ и l₂ следует, что , , где ₁ и ₂ – углы наклона прямых l₁ и l₂ к оси (Ох). Обозначим  ориентированный угол между l₁ и l₂ . По свойству внешнего угла треугольника получим  = ₂  ₁. Отсюда

. Итак, (34)

Рис. 40

Следствие. Две наклонные прямые перпендикулярны тогда и только тогда, когда

(35)

Задача. Дано: R = , l₁ : 3х + 4у +12 = 0, l₂ : 4х  7у  1 = 0.

Найти тангенс угла между прямыми l₁ и l₂. Решение. Используем формулу (34). Для этого нужно найти угловые коэффициенты данных прямых. Разрешая уравнения прямых относительно у, получим, что , . Следовательно,

Задача 13. Дано: R = , l₁ : 3х + 4у +12 = 0, l₂ : 4х + 3у  24 = 0. Найти уравнения биссектрис углов, образованных l₁ и l₂. Решение. Если l₃ и l₄ – биссектрисы данных углов, то каждая из них проходит через точку А = l₁  l₂. Координаты точки А найдём, решая систему уравнений Получим А( ). По определению биссектрисы = и = . Обозначим через к угловые коэффициенты l₃ и l₄ . 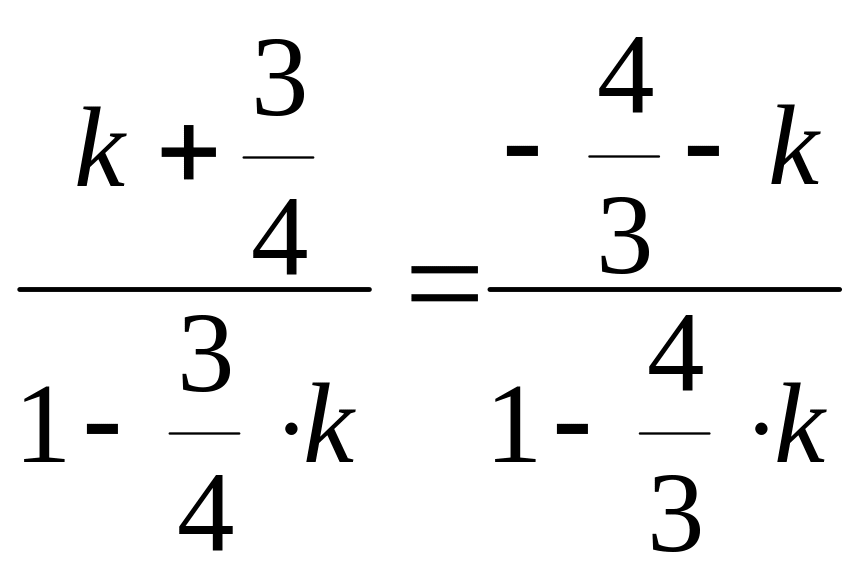Используя формулу (34), получим .Так как и , то , или . Отсюда . Следовательно, , . Используя уравнение (27), получим l₃ : (у + ) = 1(х  ). После упрощения l₃ : х  у  36 =0.

Аналогично, l₄ : (у + ) = 1(х  ). После упрощения l₄ : 7х + 7у  12 =0.