2.3.2. Приклад застосування методу Ньютона-Рафсона (модифікованого методу Ньютона)

Дана модифікація застосовує дещо іншу формулу для знаходження наступного наближення (при цьому функція має бути двічі неперервно диференційованою)

Розглянемо наступну задачу:

мінімізувати

Для того щоб визначити стаціонарну точку функції f(х), скористаємося методом Ньютона-Рафсона, поклавши :

, .

Ітерація 1. , , .

Ітерація 2. , , ,

Ітерації продовжуються доти, поки не буде виконуватися нерівність , де зазделегідь встановлена величина допустимого відхилення.

Завдання

Знайти мінімальне чи максимальне значення функції на проміжку . Точку визначити з точністю . Написати програму, передбачити вивід на екран і на друк проміжних значень обчислень, порахувати кількість ітерацій, необхідних для досягнення заданої точності.

1.19.

Ділення інтер­валу наполовину

Програма:

a=-3;

b=2;

a1=a;

b1=b;

epc =0.001;

L = b-a;

n=0;

while L > epc ,

n=n+1;

% n - kil'kist' iteracij

% Step 1

Xm = (a+b)/2

L = b-a;

fm = 2+5*Xm-10*Xm*Xm-5*Xm*Xm*Xm-Xm*Xm*Xm*Xm*Xm

% Step 2

X1 = a+L/4

X2 = b-L/4

f1 = 2+5*X1-10*X1*X1-5*X1*X1*X1-X1*X1*X1*X1*X1

f2 = 2+5*X2-10*X2*X2-5*X2*X2*X2-X2*X2*X2*X2*X2

% Step 3

if f1>fm,

b = Xm;

Xm = X1;

else

if f2>fm,

a=Xm;

Xm=X2;

end

if f2<fm,

a=X1;

b=X2;

end

end

L = abs(b-a);

end

Xs=(X1+X2)/2;

fs=2+5*Xs-10*Xs*Xs-5*Xs*Xs*Xs-Xs*Xs*Xs*Xs*Xs;

disp ('Znachennya xs');

Xs

disp ('Znachennya f(xs)');

fs

disp ('Kilkist iteracij n');

n

% Grafik funkciji

% N - kil'kist' tochok na promizhku

N=21;

h=(b1-a1)/(N-1);

for ii=1:N,

xx(ii)=a1+(ii-1)*h;

fx(ii)=2+5*xx(ii)-10*xx(ii)*xx(ii)-5*xx(ii)*xx(ii)*xx(ii)-xx(ii)*xx(ii)*xx(ii)*xx(ii)*xx(ii);

end

figure (1); hold on; plot (xx,fx,'r'); drawnow;

return

Результати виконання

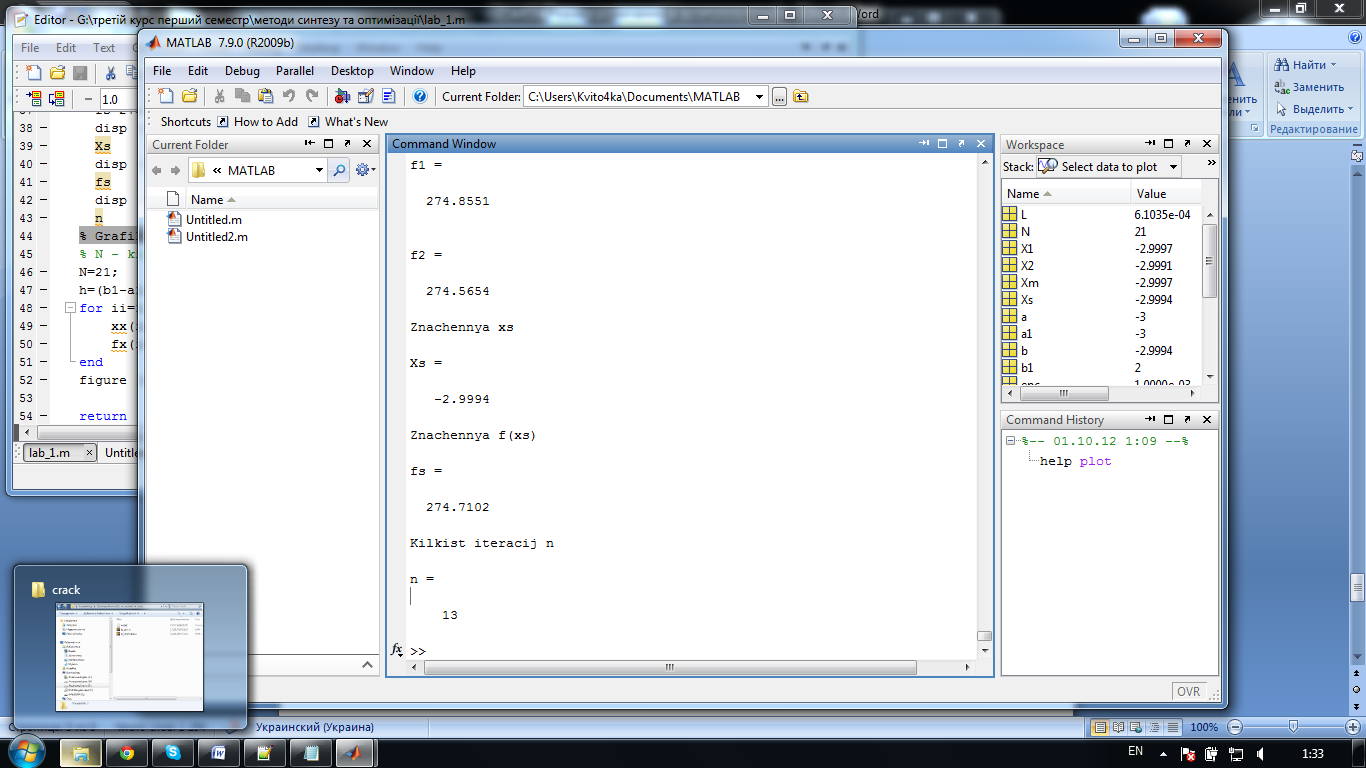
Графік функції:

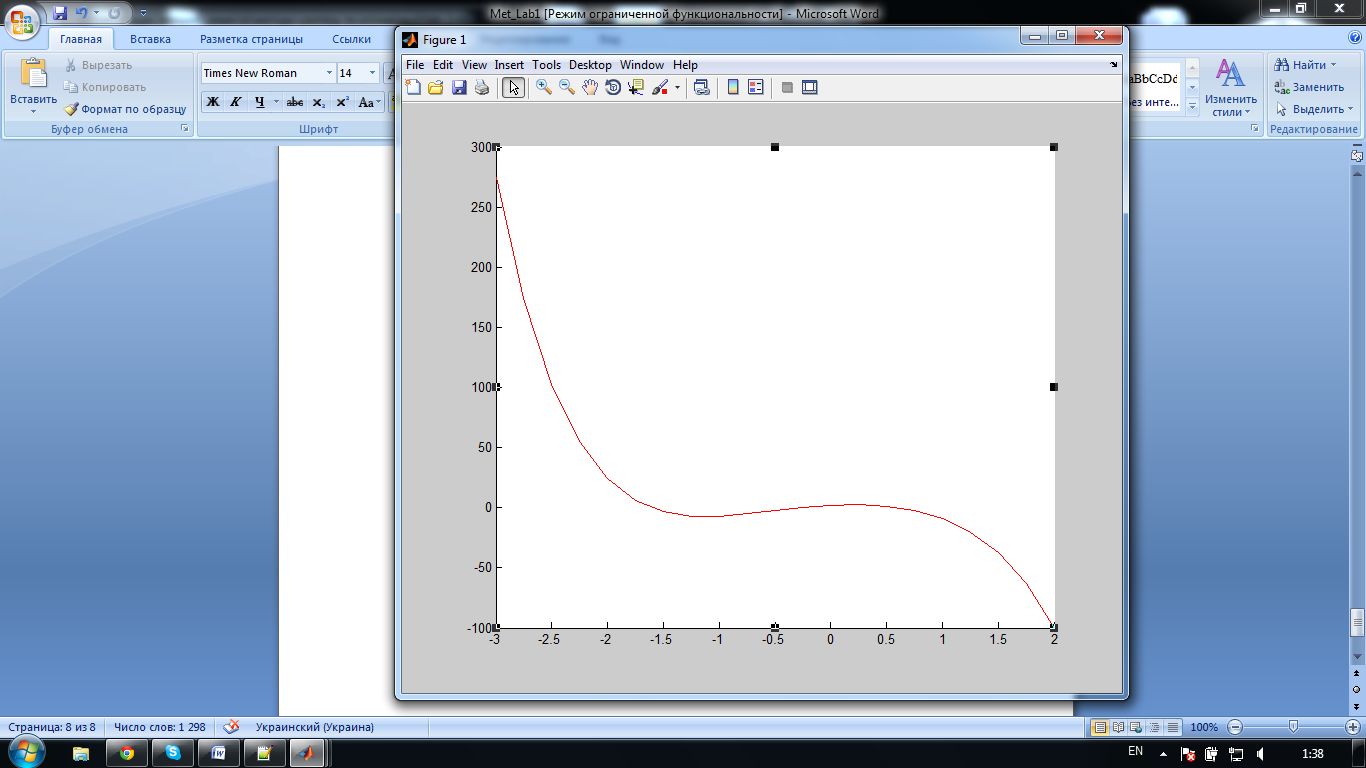
Висновок:

Виконуючи дану лабораторну роботу я вивчила основні алгоритми розв’язку одновимірних оптимізаційних задач. Написала програму, де реалізовано метод поділу інтервалу навпіл. В результаті виконання програми виявилось, що для знаходження максимуму даної функції з точністю 0,001 ,потрібно було здійснити 13 ітерацій.

8