МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

Національній університет "Львівська політехніка"

звіт

до лабораторної роботи №1

НА ТЕМУ:

Дослідження роботи методів одновимірної оптимізації

з курсу

"Методи синтезу та оптимізації"

Виконала

Студентка гр. КН-33

Нарушинська О.О.

Прийняв

Андрійчук М.І.

ЛЬВІВ 2012

1. МЕТА РОБОТИ

Вивчити основні алгоритми розв’язку одновимірних оптимізаційних задач.

2. КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

2.1. Методи виключення інтервалів

Методи пошуку, які дозволяють визначити оптиум функції однієї змінної шляхом зменшення інтервалу пошуку, носять назву методів виключення інтервалів.

Усі методи одновимірної оптимізації базуються на припущенні, що цільова функція, в допустимій області принаймні володіє властивістю унімодальності, оскільки для унімодальної функції порівняння значень та в двох різних точках ( і ) інтервалу пошуку дозволяє визначити в якому із заданих підінтервалів точка оптиуму відсутня.

2.1.1. Правило виключення інтервалів

Нехай унімодальна функція на відрізку [a, b], а її мінімум досягається в точці . Розглянемо точки і , які розташовані в наступний спосіб: а< < <b.

• Якщо > , то точка мінімуму не лежить в інтервалі (a, ), тобто ( , b).

• Якщо < , то точка мінімуму не лежить в інтервалі ( , b), тобто    (a,  ^).

Це правило дозволяє реалізувати процедуру пошуку шляхом послідовного виключення частин початкового обмеженого інтервалу. Пошук завершується тоді, коли підінтервал, що залишився зменшився до досить малих розмірів.

Основна перевага пошукових методів – вони базуються на обчисленні тільки значень функції і, отже, не вимагають виконання умови диференційованості і запису в аналітичному вигляді. Остання властивість особливо цінна при імітаційному моделюванні.

Процес застосування методів пошуку на основі виключення інтервалів включає два етапи:

• етап встановлення границь інтервалу;

• етап зменшення інтервалу.

2.1. 2. Метод поділу інтервалу пошуку наполовину

Метод поділу інтервалу пошуку наполовину дозволяє зменшити інтервал пошуку наполовину при кожній ітерації.

Знайти minF(х) на відрізку [a, b].

Крок 1. xm=(а+b)/2; L=b-a; обчислити F(xm).

Крок 2. x1=а+L/4; x2=b-L/4; обчислити і .

Крок 3.

• Якщо <F(xm), то виключити (xm, b], тобто b=xm, xm=x₁. Перейти до кроку 5.

• Якщо > F(xm), то перейти до кроку 4.

Крок 4.

• Якщо <F(xm), то виключити [a, x_m), тобто а=xm, xm=x₂. Перейти до кроку 5.

• Якщо > F(xm), то виключити [a, x₁)] і (x₂, b], тобто а=x₁, b=x₂. Перейти до кроку 5.

Крок 5. L=b-a. ЯкщоL|  то закінчити пошук. В іншому випадку повернутися до кроку 2.

( - мале, наперед задане число – точність обчислень).

2.1. 3. Метод золотого січення

Основна суть методу. Інтервал пошуку ділиться на дві нерівні частини так, щоб відношення довжини великого відрізка до довжини всього інтервалу було таке, що дорівнює відношенню довжини меншого відрізка до .

Знайти min на відрізку [a, b].

Крок 1. Обчислюємо коефіцієнт дроблення відрізка [a, b]: k=( - 1)/2.

Крок 2. x₁=а+(1-k)(b-a), обчислити .

Крок 3. x₂=а+k(b-a), обчислити .

Крок 4.

• Якщоx₂-x₁| < _ де - задана точність, то xm = (x₁+x₂)/2, обчислити 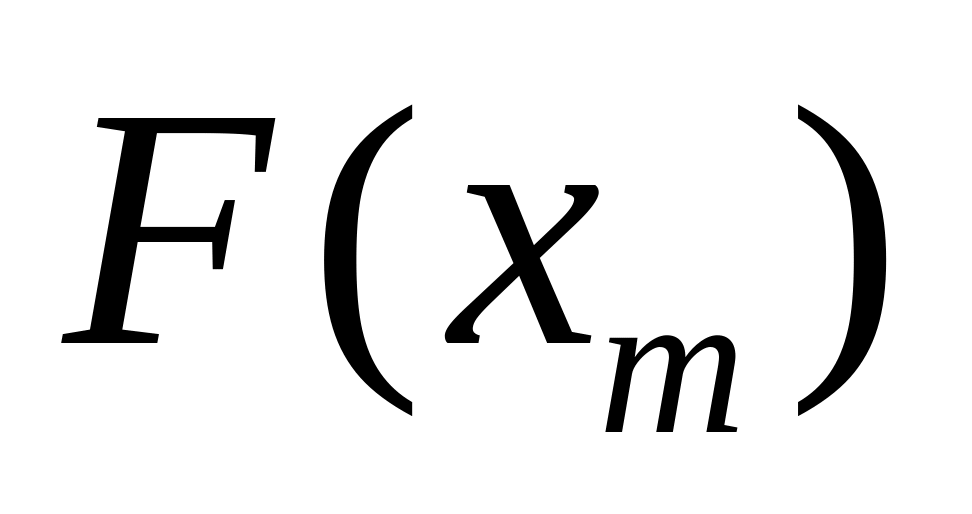і закінчити пошук.

• Якщоx₂-x₁| > _  то перейти до кроку 5.

Крок 5.

• Якщо > ,то а=x₁, x₁=x₂ і = .Перейти до кроку 3,потім до кроку 4.

• Якщо < , то b=x₂, x₂=x₁ і = . Перейти до кроку 2 і 4.

Таким чином, застосування методів виключення інтервалів накладає єдине обмеження на цільову функцію, яка досліджується - унімодальність. Отже, розглянуті методи можна використати для аналізу як неперервних, так і розривних та дискретних функцій. Логічна структура пошуку базується на простому порівнянні значень функції в двох пробних точках.