МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

Національний університет «Львівська політехніка»

Кафедра САПР

Звіт

лабораторна робота №4

на тему:

ДОСЛІДЖЕННЯ МЕТОДІВ БАГАТОПАРАМЕТРИЧНОЇ ОПТИМІЗАЦІЇ НА ПРИКЛАДІ МЕТОДІВ ПРЯМОГО ПОШУКУ

з курсу:

«Методи синтезу та оптимізації»

Виконала

ст. гр. КН-33

НарушинськаО.О

Перевірив

Андрійчук М. І.

Львів 2012

1. МЕТА РОБОТИ

Вивчити основні методи багатопараметричної оптимізації на основі алгоритмів прямого пошуку

2. КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Прямі методи

Прямі методи, або методи нульового порядку не вимагають знання цільової функції в явному вигляді. Вони не вимагають регулярності і неперервності цільової функції й існування похідних. Це є істотною перевагою при розв’язуванні складних технічних і економічних задач. При реалізації прямих методів істотно скорочується етап підготовки рішення задачі, тому що немає необхідності у визначенні перших і других похідних. Прямі методи в основному носять евристичний характер. До прямих методів відноситься цілий ряд алгоритмів, що відрізняються по своїй ефективності. Методи призначені для рішення безумовних задач оптимізації

.

Симплексний метод нелдера-міда чи пошук по деформуючому багатограннику

У процесі пошуку по симплексу здійснюється робота з регулярними симплексами. Регулярні багатогранники в просторі називаються симплексами. Для регулярний симплекс являє собою рівносторонній трикутник; при - тетраедр і т.д.

Координати вершин регулярного симплекса в - мірному просторі можуть бути визначені наступною матрицею D, у якій стовпці являють собою вершини симплекса, пронумеровані від 1 до ( ), а рядки – координати вершин, . Матриця має розмірність :

,

де:

; ;

– відстань між вершинами.

Рис. 1.

У найпростішому виді симплексний алгоритм полягає в наступному. Будується регулярний симплекс. З вершини, у якій максимальна (т.1) проводиться пряма, що проектує, через центр ваги симплекса. Потім т.1 виключається і будується новий відбитий симплекс зі старих точок, що залишилися, і однієї нової, розташованої на прямій, що проектує, на належній відстані від центра ваги.

Продовження цієї процедури, у якій щораз виключається вершина, де цільова функція максимальна, а також використання правил зменшення розміру симплекса і запобігання циклічного руху в околиці екстремуму дозволяє досить ефективно визначати мінімум для "гарних" функцій. Але для функцій типу “яру” такий пошук неефективний.

У симплексному алгоритмі Нелдера і Міда мінімізація функцій змінних здійснюється з використанням деформуючого багатогранника.

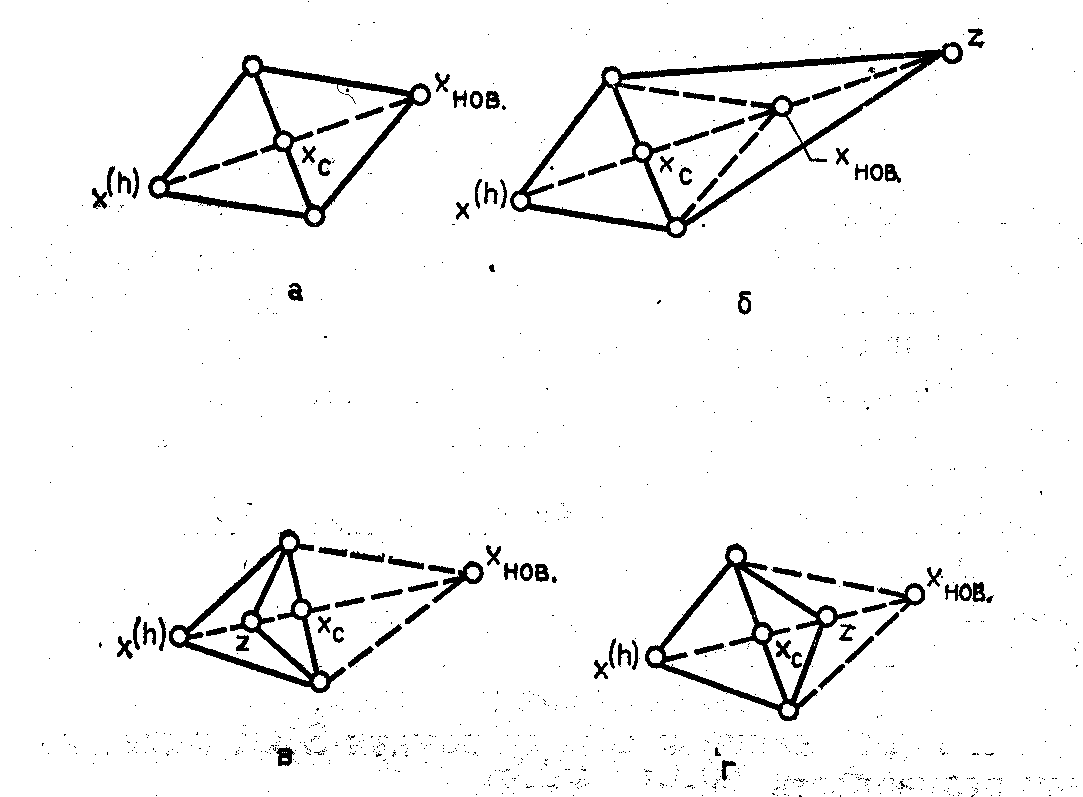
Рис. 2. Розтяг і стиск симплекса.

а – нормальне відображення , ; б – розтяг , ; в – стиск , , ; г – стиск , .

Будемо розглядати -у ітерацію алгоритму. Нехай , , є -ою вершиною в на -м етапі пошуку, , і нехай значення цільової функції у вершині . Відзначимо вершини з мінімальним і максимальним значеннями. І позначимо їхній у такий спосіб:

и.

Багатогранник у складається з вершин . Позначимо через - центр ваги вершин без точки з максимальним значенням функції. Координати цього центра обчислюються по формулі:

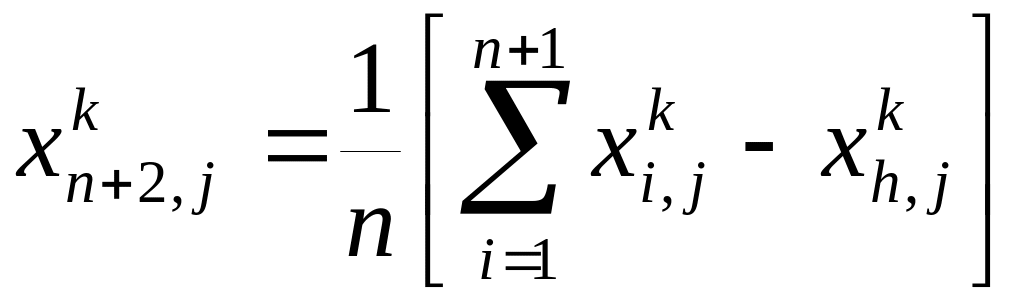, . (1)

Початковий багатогранник звичайно вибирається у виді регулярного симплекса (з вершиною в початку координат). Можна початок координат помістити в центр ваги. Процедура відшукання вершини у , у якій має краще значення, складається з наступних операцій: 1) відображення; 2) розтягання; 3) стиску; 4) редукції.

1. Відображення. Відображення – проектування точки через центр ваги у відповідності з наступним співвідношенням:

, (2)

де - коефіцієнт відображення.

Обчислюємо значення функції в знайденій точці . Якщо значення функції в даній точці , то переходимо до четвертого пункту алгоритму – операції редукції.

Якщо , то виконуємо операцію розтягання.

2. Розтягання. Ця операція полягає в наступному. Якщо (менше мінімального значення на -м етапі), то вектор розтягується відповідно до співвідношення

, (3)

де - коефіцієнт розтягання.

У протилежному випадку, якщо , то виконується операція стиску.

Якщо , то заміняється на і процедура продовжується з операції 1) при . У противному випадку заміняється на і переходимо до операції відображення 1).

3. Стиск. Якщо для , то вектор стискується відповідно до формули

,

де - коефіцієнт стиску. Після цього, точка заміняється на , і переходимо до операції відображення 1) на кроці.

4. Редукція. Якщо , то усі вектори , де зменшуються в два рази з відліком від точки по формулі

,

і переходимо до операції відображення (на початок ітераційної процедури – Крок 1. Відображення) .

Як критерій зупинки можуть бути узяті ті ж критерії, що й в інших алгоритмах. Можна також використовувати критерій зупинки наступного виду:

.

Вибір коефіцієнтів звичайно здійснюється емпірично. Після того, як багатогранник відповідним чином промасштабований, його розміри повинні підтримуватися незмінними, поки зміни в топології задачі не зажадають багатогранника іншої форми. Найчастіше вибирають , , .