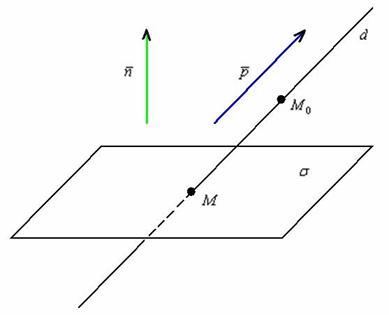
Взаимное расположение прямой и плоскости

Рассмотрим плоскость  и прямую , заданную точкой  и направляющим вектором .

Существует три варианта взаимного расположения прямой и плоскости:

1) прямая пересекает плоскость в некоторой точке ;

2) прямая параллельна плоскости: ;

3) прямая лежит в плоскости: . Да, так вот нагло взяла, и лежит.

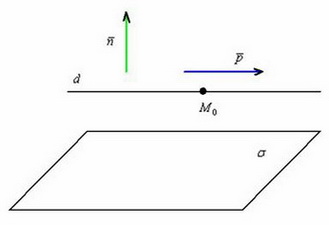
Как выяснить взаимное расположение прямой и плоскости?

Изучим аналитические условия, которые позволят нам ответить на данный вопрос. Выполним схематический чертёж, на котором прямая пересекает плоскость: Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор  не ортогонален вектору нормали  плоскости. 

Из утверждения следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: .

В координатах условие запишется следующим образом:

Если же данные векторы ортогональны, то есть если их скалярное произведение равно нулю: , то прямая либо параллельна плоскости, либо лежит в ней: 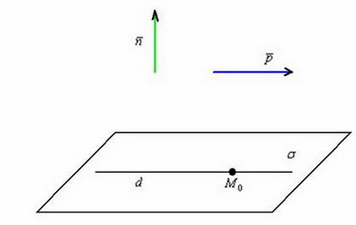Разграничим данные случаи.

Если прямая параллельна плоскости, то точка  (а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: .

Таким образом, условие параллельности прямой и плоскости записывается следующей системой:

Если прямая лежит в плоскости, то точка  (а, значит, и ЛЮБАЯ точка данной прямой) удовлетворяет уравнению плоскости: .

Аналитические условия данного случая запишутся похожей системой:

Разборки с взаимным расположением прямой и плоскости достаточно примитивны – всего в два шага. Кроме того, на практике можно обойтись даже без всяких систем. Исследование взаимного расположения прямых в пространстве, которое проводилось на уроке Задачи с прямой в пространстве, намного трудозатратнее. А тут всё проще:

Пример 1

Выяснить взаимное расположение прямой, заданной точкой  и направляющим вектором , и плоскости .

Решение: Вытащим вектор нормали плоскости: .

Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: , значит, прямая либо параллельна плоскости, либо лежит в ней.

Подставим координаты точки  в уравнение плоскости: Получено верное равенство, следовательно, точка  лежит в данной плоскости. Разумеется, и любая точка прямой тоже будет принадлежать плоскости.

Ответ: прямая лежит в плоскости

37.Комплексные числа..

Во множестве действительных чисел нельзя решить уравнение . Расширяя действительные числа, введем число   - мнимая единица: . Тогда, уравнение будет иметь решение .

П.1. Алгебраическая форма комплексного числа

Определение. Комплексным числом называется число , где x -называется действительной частью комплексного числа и обозначается ;  называется мнимой частью комплексного числа и обозначается . Такая запись комплексного числа называется алгебраической формой комплексного числа.

Пример. . , .

Определение. Модулем комплексного числа  называется величина .

Определение. Аргументом комплексного числа   называется число: . Главное значение аргумента обозначается: arg z=  или .

Пример.

Определение. Два комплексных числа ,   называются равными , если , .

Определение. Комплексное число  равно 0, если  и .

Определение. Число  называется сопряженным комплексному числу ,причем .

Пример. ; .

П.2. Тригонометрическая форма записи комплексного числа.

Комплексное число  однозначно определяется парой действительных чисел  поэтому можно установить взаимно однозначное соответствие между всевозможными точками плоскости и всевозможными комплексными числами.

Тогда, комплексное число можно изобразить с помощью точки плоскости, координаты которой   - абсцисса,   - ордината. Это геометрическая, интерпретация комплексного числа.

Рис. 1.

Тогда ось OX – где откладываются действительные части числа  называется действительной осью.

OY – где откладывают мнимые части числа  называется мнимой осью.

Такую плоскость будем называть «комплексной плоскостью».

 Действительной и мнимой частям комплексного числа  можно также поставить в соответствие координаты радиус-вектора .

Рис. 2.

Т.е. комплексное число можно изобразить с помощью вектора .

Тогда, длина вектора  - есть модуль комплексного числа ; а угол  есть аргумент комплексного числа:

.

Из определения модуля и аргумента следует, что если , то , .

Тогда, любое комплексное число, отличное от нуля, можно представить в тригонометрической форме:

Пример. Представить комплексное число в тригонометрической форме:

1)    

2)    

П.3. Показательная форма комплексного числа.

 и  связаны формулой Эйлера: .

Тогда от тригонометрической формы комплексного числа можно перейти к показательной форме:

.

Тогда   Складывая и вычитая, легко получить

.

Примеры. Записать комплексное число в показательной форме.

1)    

2)    

П.4. Алгебраические операции над комплексными числами.

Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов; учитывая при этом, что  и т.д.

1)     Рассмотрим операции над комплексными числами в алгебраической форме

Пусть

.

Замечание.

2)     Рассмотрим операции над комплексными числами в тригонометрической форме:

Пусть

.

Формула Муавра: .

.

 имеет  позиций в области комплексных чисел.

Из формулы для  видно, что все  различных значений величины  имеют один и тот же модуль равный . А так как , то точки соответствующие значениям , являются вершинами правильного -угольника, вписанного в окружность радиуса  с центром в начале координат.

3)     алгебраические операции в показательной форме:

.

Примеры.

1)      - в алгебраической форме.

,

 - тригонометрическая форма.

.

.

.

 П.4. Линии и области в комплексной плоскости

 Чтобы построить линию в комплексной плоскости нужно перейти к записи уравнения этой линии в действительных координатах: z=x+iy, x=Rez, y=Imz, IzI= .

 Примеры.

1. Построить линию, заданную уравнением Re(z+2)=3. Перейдем к декартовым координатам, получим Re(x+iy+2)=3x+2=3x=1. Это уравнение прямой параллельной мнимой оси.

2. Построить линию, заданную уравнением Iz-3iI=2. Перейдем к декартовым координатам, получим Ix+iy-3iI=2 Это уравнение окружности с центром в точке (0; 3) и радиуса равного 2.

3. Записать уравнение линии в комплексной форме: . Выразим декартовы координаты через комплексную переменную, получим  или  Это уравнение прямой с выколотой точкой (0; 0) в комплексной форме.

 Чтобы построить область в комплексной плоскости нужно в неравенстве, определяющем эту область заменить комплексную переменную z действительными переменными x и y.

 Примеры.

1. Определить область, заданную неравенствами: 2 Im(z-i)3. Перейдем к декартовым координатам, получим 2 y-133 y 4. Это область, заключенная в полосе между прямыми y=3 и y=4.

2. Определить область, заданную неравенством Iz-iI<Iz+3I. Перейдем к декартовым координатам, получим

Это часть плоскости, расположенная выше прямой y=-3x-4.

3. Определить область, заданную неравенством Iz-3+2iI>2. Это часть плоскости, расположенная вне круга

Правило умножения двух комплексных чисел позволяет получить замечательное соотношение, открытое английским математиком А. де-Муавром (1667–1754).

Найдем квадрат комплексного числа z = r(cos  + i sin ), т.е. результат произведения этого числа на само себя:

z² = z•z = r(cos  + i sin )•r(cos  + i sin ).

По правилу умножения двух комплексных чисел имеем: z² = r²(cos  + i sin )² = r²(cos 2 + i sin 2).

Повторяя n раз операцию возведения в степень числа z, мы получим формулу n-ой степени числа z:

zⁿ = rⁿ(cos n + i sin n),

где n – натуральное число.

Методом математической индукции можно доказать эту формулу. Она представляет собой обобщение формулы, открытой Муавром. Муавр открыл ее для случая, когда модуль комплексного числа z равен 1. Формула Муавра имеет вид:

(cos  + i sin )ⁿ = cos n + i sin n,

где n  N.

С помощью формулы Муавра можно вывести многие полезные соотношения, в частности, между тригонометрическими выражениями.

Формула Муавра позволяет найти значения корней любой (n-й) степени в поле комплексных чисел. Под корнем n-й степени из числа z понимают такое число a, n-я степень которого равна z: aⁿ = z. Ограничимся рассмотрением вопроса об извлечении корня n-ой степени из 1 в поле комплексных чисел. Другими словами, будем рассматривать вопрос о решении уравнения zⁿ = 1, где n  N в поле комплексных чисел. Например, корень квадратный из числа 1 имеет два значения: 1 и – 1. Действительно, 1² = 1 и (– 1)² = 1. Корень четвертой степени из числа 1 в поле комплексных чисел имеет четыре значения: два действительных, 1 и – 1, и два мнимых, i и – i. Этот факт можно установить проверкой: 1⁴ = 1 и (– 1)⁴ = 1; i⁴ = 1 и (– i)⁴ = 1.

Эти два примера наводят на предположение о том, что корень кубический из 1 в поле комплексных чисел должен иметь 3 значения; корень пятой степени из 1 должен иметь пять значений и т.д. Корень n-й степени из числа 1 в поле комплексных чисел должен иметь n значений.

Это предположение оказывается верным. Воспользовавшись формулой Муавра, можно доказать, что уравнение zⁿ = 1 в поле комплексных чисел имеет ровно n решений, т. е. корень n-й степени из числа z в поле комплексных чисел имеет ровно n значений. Эти значения корня изображаются вершинами правильного n-угольника, вписанного в единичную окружность, причем точка (0; 1) является одной из вершин этого многоугольника.

При помощи формулы Эйлера можно определить функции и следующим образом:

,

.

Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть , тогда:

,

.

Известное тождество Эйлера, связывающее пять фундаментальных математических констант:

является частным случаем формулы Эйлера при .

Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: .

Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: , . Геометрический смысл данной формулы следующий: при возведении числа в степень его расстояние до центра возводится в степень , а угол поворота относительно оси увеличивается в раз.

Формула возведения в степень верна не только для целых , но и для вещественных. В частности, комплексная запись числа позволяет находить корни любой степени из любого комплексного числа, что и используется при доказательстве основной теоремы алгебры: «Многочлен степени имеет ровно комплексных корней».