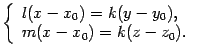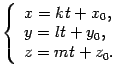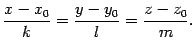34. Нормальное уравнение плоскости Расстояние от точки до плоскости . Условия принадлежности 4 точек одной плоскости.

В векторной форме уравнение плоскости имеет вид

 

, .

 

 Если нормальный вектор плоскости – единичный,

, ,

 

 

тогда уравнение плоскости можно записать в виде

 

 

(нормальное уравнение плоскости).

– расстояние от начала координат до плоскости, , , _– направляющие косинусы нормали

  , , ,

 

 

где – углы между нормалью плоскости и осями координат соответственно.

Общее уравнение плоскости (8) может быть приведено к нормальному виду умножением на нормирующий множитель , знак перед дробью противоположен знаку свободного члена в (8).

Расстояние от точки до плоскости (8) находится по формуле, полученной подстановкой точки в нормальное уравнение

.

 

Пример 16. Даны точки , , . Составить уравнение плоскости, проходящей через перпендикулярно вектору . Привести его к нормальному виду.

Решение. Вектор имеет вид . По формуле (6) составим общее уравнение искомой плоскости

.

Найдем нормирующий множитель

.

 

Умножая уравнение плоскости почленно на нормирующий множитель, получим нормальное уравнение плоскости

,

 

где коэффициенты при – соответствующие направляющие косинусы нормали, расстояние от начала координат до плоскости .

Ответ: общее уравнение плоскости: ; нормальное уравнение: .

Пример 17. Даны точки , , . Найти расстояние от точки до плоскости .

Решение. Составим уравнение плоскости

,

 

.

 

Расстояние от до плоскости

.

 

Ответ: расстояние от до плоскости ед. длины.

 

35.Уравнение прямой в пространстве..

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

Итак, если уравнения двух непараллельных плоскостей -- и , то прямая, являющаяся их линией пересечения, задается системой уравнений

(11.11)

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.

Уравнения (11.11) называют общими уравнениями прямой в пространстве.

        Замечание 11.2   Любые попытки с помощью преобразований уравнений системы (11.11) получить одно (линейное) уравнение, задающее прямую, обречены на неудачу. Одно уравнение -- это уравнение плоскости.         

Общие уравнения прямой "неудобны" для получения информации о положении прямой.

Например, чтобы найти координаты какой-нибудь точки на прямой, нужно провести довольно сложные вычисления. А именно, задать произвольно какую-нибудь координату, подставить ее в систему (11.11) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты. Причем может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.

        Пример 11.2   Требуется найти какую-нибудь точку на прямой

Решение. Положим . Получим систему

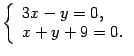
Решая ее, находим , .

Ответ: .         

Можно задать прямую в пространстве и другим способом.

Ненулевой вектор, лежащий на прямой (параллельный ей) называется направляющим вектором прямой.

Пусть для прямой известны ее направляющий вектор и точка , лежащая на этой прямой. Пусть  -- произвольная (текущая) точка прямой . Обозначим через и r радиус-векторы точек и соответственно (рис. 11.11).

Рис.11.11.Векторное уравнение прямой

Тогда вектор коллинеарен вектору p и, следовательно, , где  -- некоторое число. Из рис. 11.11 видно, что

(11.12)

Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра мы будем получать новую точку на прямой .

        Замечание 11.3   Если в качестве параметра взять время, то точка будет двигаться по прямой со скоростью , причем в момент времент ее положение совпадает с точкой . Вектор скорости точки совпадает с вектором p.         

От векторного соотношения (11.12) перейдем к соотношениям координат. Так как  -- координаты точки , то , , . Из формулы (11.12) получим

(11.13)

Полученная система уравнений называется параметрическими уравнениями прямой.

Обратим внимание на то, что по параметрическим уравнениям легко установить направляющий вектор прямой и координаты одной из ее точек. Коэффициенты перед параметром дают координаты направляющего вектора, а свободные члены в правой части -- координаты точки на прямой.

Так как направляющий вектор прямой определяется с точностью до умножения на число, отличное от нуля, а в качестве точки можно взять любую точку прямой, то одна и та же прямая может задаваться бесконечным множеством систем параметрических уравнений. Причем разные системы могут быть не похожими друг на друга.

Из уравнений (11.13) выразим параметр :

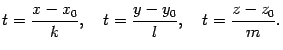
Так как во всех трех соотношениях параметр имеет одно и то же значение, то

(11.14)

Эти уравнения называются каноническими¹ уравнениями прямой.

        Замечание 11.4   В канонических уравнениях прямой допускается в знаменателе писать 0. Это не означает, что можно выполнить деление на 0. Просто из канонических уравнений мы получаем информацию о том, что направляющий вектор прямой имеет координаты , из которых одна нулевая.         

        Пример 11.3   Прямая с каноническими уравнениями

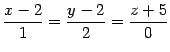
имеет направляющий вектор .         

        Замечание 11.5   Канонические уравнения прямой (11.14) нельзя рассматривать как одно уравнение (в них два знака "=" и следовательно, два уравнения). Они составляют своеобразным способом записанную систему из двух уравнений