27.Интервальные оц-ки парам-ов распр-ия

Интерв-ой оц-ой наз.оц-ка,ктр опр-ся двумя числами или концами инт-ов.Чем меньше δ,тем оц-ка точнее. Надёжностью (доверительной вероятностью) оценки Ѳ по Ѳ* называют вероятность γ, с которой осуществляется неравенство 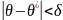. Обычно надёжность задаётся наперёд, причём в качестве γ берут число, близкое к единице. Наиболее часто задают надёжность, равную 0,95, 0,99 и 0,999.

Доверительным называют интервал (Ѳ*-δ, Ѳ*+δ), который покрывает неизвестный параметр с заданной надёжностью γ.

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение  этого распределения -. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью . Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки  к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением . 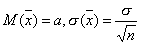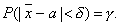Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами  .Потребуем, чтобы выполнялось равенство   Заменив Х и «сигму», получим

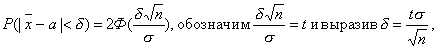
28) Статистическая проверка статистических гипотез

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, в этой гипотезе идет речь о виде предполагаемого распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр равен определенному значению , выдвигают гипотезу . Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного распределения.

Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и многие другие.

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Следовательно, эти гипотезы целесообразно различать.

Нулевой (основной) называют выдвинутую гипотезу Н0.

Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.

Различают гипотезы, которые содержат только одно и более одного предположений.

Простой называют гипотезу, содержащую только одно предположение. Например: если – параметр показательного распределения, то гипотеза Н0: l= 5 – простая.

Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез. Сложная гипотеза Н:l > 5 состоит из бесчисленного множества простых вида Нi:l = bi, где bi – любое число, большее 5.

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина , распределение которой известно полностью или частично. Тогда любое утверждение, касающееся называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

Статистическая гипотеза, однозначно определяющая распределение , то есть , где какой-то конкретный закон, называется простой.

Статистическая гипотеза, утверждающая принадлежность распределения к некоторому семейству распределений, то есть вида , где — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза , называемая конкурирующей или альтернативной.

Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.

В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема из распределения . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной (см. Последовательный статистический критерий).