24.Матем-ая статистика.Осн-ые опред-ия
К зад-ам стат-ки отн-ся:1)ук-ие сп-ба сбора ст-их свед-ий,пол-ых в рез-те набл-ий или спец-но пост-ых эксп-ов
2)разр-ка методов ан-за стат-их данных:а)оц-ка неизв-ой в-ти соб-ия
б)оц-ка неизв-ой ф-ии распр-ия
в)оц-ка пар-ов распр-ия,вид ктрх неизв-ен
г)оц-ка зав-ти сл-ой вел-ны от 1 или неск-их сл-ых вел-ин
д)пров-ка стат-их гипотез о виде неизв-го распр-ия о вел-не пар-ов распр-ия,вид ктрг изв-ен.
Выб-ой сов-ью или выб-ой наз.сов-ть сл-но отобр-ых объектов.
Генер-ой сов-ью наз.сов-ть объектов их ктрх произв-ся выборка.
Объемом сов-ти выб-ой или генер-ой наз.число объектов этой сов-ти.
Выб-ой с повт-ми наз. тк выб-ку,при ктр отобр-ый объект перед отбором след-го возвр-ся в генер-ую сов-ть.
Выб-ой без повт-ия наз.выб-ку,при ктр об.в ген-ую сов-ть не возвр-ся.
Стат-им распр-ем выборки наз.перечень вар-ов возр-их в пор-ке и соотв-их им частот или относ-ых частот.
Эмпирической ф-ей распред-ия наз.ф-ию F*(x),опред-ую для кждг х частоту распр-ияᶳ.В отл-ие от импер-ой ф-ии распр-ия выборки ф-ию F(x) наз.теорет-ой ф-ей распр-ия.
25) Графические представления статистических рядов
1)
Вариационным
(статистическим) рядом
называется таблица, первая строка
которой содержит в порядке возрастания
элементы
,
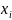а вторая – их частоты
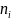(относительные частоты
).
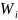2)
Пусть из генеральной совокупности
извлечена выборка, причём
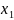наблюдалось
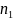раз,
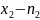раз,
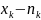раз и
– объём выборки. Наблюдаемые значения
называются вариантами, а последовательность
вариантов, записанных в возрастающем
порядке, - вариационным
(статистическим) рядом.
Статистическим распределением выборки называют перечень вариантов и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Полигон и гистограмма статистического ряда.
Полигоном
частот называют
ломаную, отрезки которой соединяют
точки
,
,
…,
.
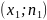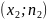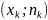Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки
,
,
…,
.
(
,
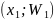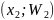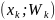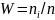где n
– объём выборки).
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
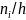(плотность частоты).
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
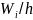(плотность относительной частоты).
26.Точечные оц-ки парам-ов распр-ия
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Виды: несмещённая, смещённая, эффективная, состоятельная.
Классификация точечных оценок (состоятельные, несмещённые, эффективные).
Состоятельной
называют статистическую оценку, которая
при
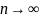стремится по вероятности к оцениваемому
параметру.
Несмещённой
называют статистическую оценку
,
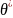математическое ожидание которой равно
оцениваемому параметру
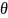при любом объёме выборки, т.е.
.
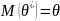Эффективной называют статистическую оценку, которая (при заданном объёме выборки n) имеет наименьшую возможную дисперсию.