17.Случайные вел-ны.Ф-ия распред-ия

Под случайной величиной (СВ) понимают величину, которая в результате опыта принимает некоторое числовое значение, причём неизвестно заранее, какое именно.

Виды СВ: а) СВ называется дискретной, если множество 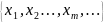ее возможных значений конечно или счетно (т.е. если все значения можно пересчитать).

б) СВ называется непрерывной, если её функция распределения непрерывна на всей числовой оси. Непрерывная СВ принимает все значения из некоторого интервала или системы интервалов на числовой оси.

Функцией распределения случайной величины называется функция   ,

определяющая вероятность того, что случайная величина примет значение, меньшее .

Свойства функции распределения:

а) функция распределения принимает значения только из отрезка [0,1]: 0 ≤ F(x) ≤ 1;

б) F(x) – неубывающая функция, т.е. если x₂ > x₁, то F(x₂) > F(x₁) ;

в) F(- ∞ ) = 0; F(+ ∞) = 1;

г) вероятность того, что случайная величина примет значение из интервала (причем ), равна ;

д) F(x) непрерывна слева, т. е. F(x) = F(x – 0).

18.Непрерывные случ.Вел. Плотность вероятности

Функция распределения представляет собой универсальный способ задания СВ в том смысле, что она существует только для дискретной СВ, а плотность распределения – только для непрерывной.

Для непрерывной СВ функция распределения F(x)=P(ξ<x) непрерывна в любой точке числовой прямой. Более того, P(ξ=x₀)=0, т.е. вероятность того, что непрерывная СВ примет заранее указанное значение, равна нулю.

F_(x) можно представить в виде интеграла

Ф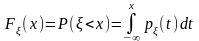 ункция 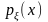называется функцией плотности распределения вероятностей.

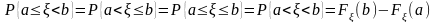
Функция называется функцией плотности распределения вероятностей.

Из определения вытекают свойства функции плотности распределения :

1.Плотность распределения неотрицательна: .

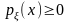_{2. Интеграл по всей числовой прямой от плотности распределения вероятностей равен единице:}

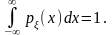
3. В точках непрерывности плотность распределения равна производной функции распределения: .

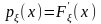4. Плотность распределения определяет закон распределения случайной величины, т.к. определяет вероятность попадания случайной величины на интервал :

.

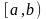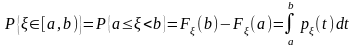5. Вероятность того, что непрерывная случайная величина примет конкретное значение 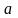равна нулю: 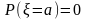. Поэтому справедливы следующие равенства:

19.Числовые хар-ки сл.Вел.И их св-ва

Математическое ожидание для непрерывно распределенных случайных величин определяется по форму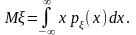ле При этом интеграл, стоящий справа, должен абсолютно сходиться. Пусть  имеет плотность р(х) и (х) - некоторая функция. Математическое ожидание величины () можно вычислить по формуле

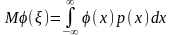, если интеграл, стоящий справа, абсолютно сходится.

Дисперсия  может быть вычислена по формуле 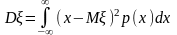, а также, как и в дискр-ом случае, по ф-л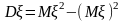е , где

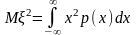
20.Осн-ые з-ны распр-ия дискр-ых случ.вел-ин

Биномиальный закон распределения. Случайная величина , распределенная по биномиальному закону, принимает значения:

0 , 1, 2, …, n с вероятностями, определяемыми по формулам Бернулли:

Числовые хар-ки: Математическое ожидание: . Дисперсия: .

Закон распределения Пуассона. Случайная величина , распределенная по закону Пуассона, принимает бесконечное счетное число значений: 0, 1, 2, …, m, …, с соответствующими вероятностями, определяемыми по формуле Пуассона

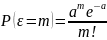При и биномиальный закон распределения приближается к закону распределения Пуассона, где a=np

Математическое ожидание M(ξ) = Дисперсия D(ξ) = a.

21.Осн-ые з-ны распр-ия непр-ых сл-ых вел-ин

Равномерное распределение. Непрерывная случайная величина  имеет равномерное распределение на отрезке [a,b], если плотность распределения р_(x) сохраняет постоянное значение на этом промежутке:

Ф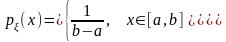 ункция распределения F_(x) равномерно распределенной случайной величины равна F_(x)=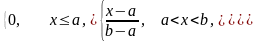

Математическое ожидание и дисперсия ; .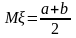

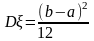Показательное (экспоненециальное) распределение. Непрерывная случайная величина , принимающая неотрицательные значения, имеет показательное распределение с параметром >0, если плотность распределения вероятностей случайной величины равна

р_(x)=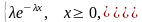

Функция распределения показательного распределения имеет вид

F_(x)=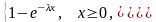

а математическое ожидание и дисперсия равны М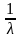= , D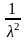= .