
- •3.Геом-ий метод реш-ия з-чи лин-го пр-ия
- •4) Симплекс-метод решения злп в норм. Форме
- •5.Теория двойств-ти в лин-ом прогр-ии
- •6.Транспортная задача.Построение первоначального плана
- •7.Транспортная задача.Метод потенциалов
- •8.Элементы динамического программирования
- •9.Задача выбора кратч-го пути на трансп-ой сети
- •11.Классическое опр-ие вер-ти
- •12.Геометр-ое опр-ие вер-ти
- •13.Теоремы сложения и умножения вер-ей
- •15.Схема незав-ых исп-ий Бернулли
- •17.Случайные вел-ны.Ф-ия распред-ия
- •18.Непрерывные случ.Вел. Плотность вероятности
- •19.Числовые хар-ки сл.Вел.И их св-ва
- •22.Системы двух сл-ых вел-ин
- •24.Матем-ая статистика.Осн-ые опред-ия
- •25) Графические представления статистических рядов
- •26.Точечные оц-ки парам-ов распр-ия
- •27.Интервальные оц-ки парам-ов распр-ия
- •28) Статистическая проверка статистических гипотез
- •29) Критерий согласия Пирсона
- •30) Осн. Понятия дисперс, корреляцио, регре анализа. М-д наим-их кв-ов.
11.Классическое опр-ие вер-ти
Вероятность
события ![]() равна
отношению числа случаев
равна
отношению числа случаев ![]() ,
благоприятствующих ему, из общего
числа
,
благоприятствующих ему, из общего
числа ![]() единственно
возможных, равновозможных и несовместных
случаев к числу
, т.
е.
единственно
возможных, равновозможных и несовместных
случаев к числу
, т.
е.
![]() (
(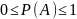 .)
.)
12.Геометр-ое опр-ие вер-ти
Пусть
на плоск-ти есть пл-ая си-ма коорд-т и
нар-ем ф-ру,и внутри ее тоже,часть
простр-ых соб-ий.Пусть на пр-во эл-ых
соб-ий сл-ым обр-ом брос-ся мат-ая
точка.Если эта т-ка ок-ся вн-ри ф-ры А,то
мжн считать,что это соб-ие произошло,если
не попадает,то сч-ем,что соб-е А пр-ло.Н-ти
в-ть со.А.
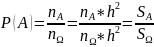
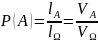

![]()
Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.
13.Теоремы сложения и умножения вер-ей
Теорема сложения вероятностей
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В). В случае, когда события А и В совместны, вер-ть их суммы выражается формулой Р (А +В) = Р (А) + Р (В) – Р (АВ), где АВ – произведение событий А и В.
Теорема умножения вероятностей
Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого: Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).
14.Ф-ла полной вер-ти
Если об обстановке опыта можно сделать n исключающих друг друга предположений (гипотез)
Н1, Н2, ..., Нn и если событие А может появиться только при одной из этих гипотез, то вероятность события Авычисляется по формуле полной вероятности:
Р(А) = Р(Н1) Р(А/Н1) + Р(Н2) Р(А/Н2) +...+ Р(Нn) Р(А/Нn).
15.Схема незав-ых исп-ий Бернулли
Последовательность
n
независимых в совокупности испытаний
называется схемой
Бернулли,
если при каждом испытании возможны
только два исхода: появление события А
(успех) и его непоявление
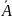 (неуспех), причём вероятность появления
события А в каждом из n независимых
испытаний постоянна и равна p.
(неуспех), причём вероятность появления
события А в каждом из n независимых
испытаний постоянна и равна p.
В
схеме Бернулли вероятность
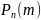 того, что в n
испытаниях событие А наступит ровно m
раз, вычисляется по формуле
Бернулли:
того, что в n
испытаниях событие А наступит ровно m
раз, вычисляется по формуле
Бернулли:
 ,
где q=1-p;
,
где q=1-p;
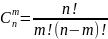 ;
n!=n·(n-1)·…·2·1,
0!=1.
;
n!=n·(n-1)·…·2·1,
0!=1.
16.Лок-ая и инт-ая т-мы М.-Л.Т-ма Пуассона
Если в схеме независимых испытаний Бернулли число испытаний n велико, а вероятности успеха и неудачи не малы (например, 0,1<p<0,9), то вероятность Pn(m) появления ровно m успехов в n испытаниях вычисляется по формуле (локальная теорема Муавра-Лапласа):
Pn(m)=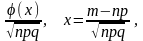 где
(х)=
где
(х)= .
Функция (х)
– четная и для положительных значений
х составлена таблица ее значений.
.
Функция (х)
– четная и для положительных значений
х составлена таблица ее значений.
Если
в схеме Бернулли p
существенно отличается от 0 и 1, а n
достаточно велико, то вероятность
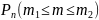 того, что в n
независимых испытаниях событие А
наступит не менее
того, что в n
независимых испытаниях событие А
наступит не менее
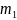 раз, но менее
раз, но менее
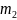 раз, вычисляется по интегральной
формуле Муавра-Лапласа:
раз, вычисляется по интегральной
формуле Муавра-Лапласа:
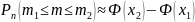 ,
где
,
где
 – функция Лапласа,
– функция Лапласа,
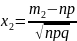 ,
,
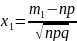 ,
причём Ф(-х)=-Ф(х), Ф(х)≈0,5 при х≥5.
,
причём Ф(-х)=-Ф(х), Ф(х)≈0,5 при х≥5.
Формулы Муавра-Лапласа, как правило, используются, если 0,1<p<0,9, и дают хорошие результаты, если npq велико (>=20).
Если
в схеме Бернулли вероятность p
появления события А в каждом из n
независимых испытаний очень мала, а
число испытаний n
достаточно велико, то вероятность
вычисляется приближенно по формуле
Пуассона:
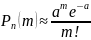 ,
a=n·p.
,
a=n·p.
Эту формулу обычно применяют в тех случаях, когда а ≤ 10.
