7.Транспортная задача.Метод потенциалов

а1+а2…аn-сум.запас пр-ии пр-ля

b1+b2…bn-сум.потр-ти в пр-ии

Если рав-во есть(мжд запас.и потр.),то это рав-во наз.усл-ем баланса.Известно,если з-ча вып-ся,то тк трансп.з-ча всегда имеет реш-ие и наз. закр-ой трансп.з-ей.Если усл-ие баланса не вып-но,то мы не смжм вып-ть одновр.усл-ие 1,2 в пост-ке тр-ой з-чи,тк трансп-ая з-ча наз.откр-ой трансп.з-ей.

Каждому поставщику (каждой строке) поставим в соответствие некоторое число

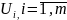, называемое потенциалом поставщика, а каждому потребителю (каждому столбцу – некоторое число 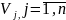называемое потенциалом потребителя.

Числа 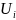и 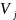выбираем так, чтобы в любой занятой клетке выполнялось равенство

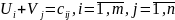
Невырожденный опорный план содержит m+n-1 заполненную клетку, поэтому для него можно составить систему m+n-1 независимых уравнений с m+n неизвестными. Уравнений на одно меньше, чем неизвестных, поэтому одному из неизвестных нужно придать произвольное значение, тогда m+n-1 неизвестных потенциалов определяются одназначно.

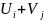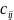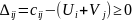Далее для каждой свободной клетки вычислим «косвенные » тарифы и сравним их со стоимостью . Если для всех свободных клеток то план оптимальный. Если хотя бы для одной клетки не выполняется, то план неоптимален и следует переходить к новому базисному плану

8.Элементы динамического программирования

Динам-ое прогр-ие-метод нах-ия оптим-ых реш-ий з-чи с многошаг-ой или многоэт-ой стр-ой.

Ос-ти з-ч,реш-ых мет-ми дин.прогр.:

1)рассм.некот.си-ма,сост-ие ктр на кжд шаге или этапе опред-ся вект-ом хi,i=1,n,дальн-ие изм-ие сост-ия дн си-мы зав-ит от днг сост-ия хi,и не зав-ит от того,ккм обр-ом си-ма пришла в это сост-ие.Тк си-мы наз.си-ми без последействия.

2)на кждм шаге выбир.одно реш-ие или упр-ие ui под д-ем ктрг си-ма прих-ит от пред-го сост-ия хi-1→xi,т.е.сост-ие хi–есть ф-я от предыд.сост.си-мы и принятого реш-я ui;xi=xi(xi-1,ui).

3)Д-ия на кждм шаге св-но с опр-ем выйгр-ем д-да или потерями,ктр зав-ят от сост-ия на начало этапа и прин-го реш-ия.zi=zi(xi-1,ai).

4)На векторы сост-ия и упр-ие м.б.наложены огр-ия,объед-ие ктрх сост.область доп-ых огр-ий з-ч.

5)В ткх з-ах треб-ся н-ти тк доп-ое управл-ие ui для кждг шага i,чт.пол-ть экстрем-ое зн-ие целевой ф-ии за все n шагов ui,i=1,n.

1 из особ.реш-я дин.з-ч явл.то,что реш-я получ.обычно от посл-го этапа к 1-му.Пр-р:условно-оптимальное упр-ие.

Дин.прогр.осн-но на след.2 фунд.принц.:

1)Пр-ип опт-ти Беллмана:оптим.стр-ия обл-ет ткм св-ом,что ккв бы они были на-е сост-я и начальн.реш-я,посл-ие реш.прин-ся исходя из опт-ой стр-ии с учетом сост-ия,вытек-го из 1-го реш.

9.Задача выбора кратч-го пути на трансп-ой сети

На трансп.сети в п.А не длжн вести ни 1стр-ка,а из В ни1не длжн выходить.Разобьем вершины на группы.К в-ам 1 ур.отн-ем в-ны,в ктр не вх-ит ни 1стр-ка.Выч-ем все стр-ки из 1гр.,внесем к в-ам 2гр.в-ны,в ктр не вх-ит ни 1стр-ка.К в-ам 3гр.отн-ем в-ны,в ктр не вх-ит ни1стр-ка и т.д.

10.ТВ.Осн-ые опр-ия

ТВ св-на с пон-ем случ-го экспер-та.Эксп-ты дел-ся на 2 кл-са:

1)детерминированные эксп.,в этом кл-се эксп-ов при вып-ии 1 и тг же комплектов усл-ий,при повт-ии этих эксп-ов получ.оди и тж рез-ты.

2)в отл-ии от детерм-ых эксп.,в случ-х эксп.,при вып-ии 1 и тг же компл-са усл-ий м.появл.противор.рез-ты. Т.о.случ.эксп.-эксп.,в ктрм при вып-ии 1 и тг же компл.усл0ий мы не мжм заранее предсказ.рез-т.

Осн.опр.:1)Элемент.соб-ем или эл-ым исходом наз.конкретный рез-т сл-го эксп-та.2)Простр-ом элем-ых соб-ий мы наз.множ-во всех принц-но возм-ых эл-ых исх-ов днг эксп-та.Прост-во эл.соб-ий дел-ся на:конечные,сод-ат кон-ое число;беск-ые.Если удается занумерить кжд эл-нт этого простр-ва,то счетнобесконечн.,если нет,то несчетн.3)Случ.соб.или просто соб.наз.произв.подмнож-во пр-ва жем-х соб-ий.4)Будем гов-ть,что в случ.эксп.произ.соб.А,если жем.исход этого эксп-та принадл.соб.А.5)невозм-м соб-ем б.наз.пустое подмн-во прост-ва элем-х соб-ий.6)Достав-ие соб-емΩназ.подмнож-во пр-ва эл.соб.совпад-ие его всем пр-ом эл.соб.7)Соб-ем А¯наз.соб-е против-е соб-ю А,если оно сост.из эл.исх-ов,ктр прин-ат пр-ву эл.соб.Ω,но не принадл.соб.А.Ф-лы Моргена:АВ¯=А¯+В¯;А+В¯=А¯В¯.