1. Основные задачи математического программирования.

2. Линейное программирование. Формы ЗЛП.

3. Геометрический метод решения ЗЛП.

4. Симплекс-метод решения ЗЛП в нормальной форме.

5. Теория двойственности в линейном программировании.

6. Транспортная задача. Построение первоначального плана.

7. Транспортная задача. Метод потенциалов.

8. Элементы динамического программирования.

9. Задача выбора кратчайшего пути на транспортной сети.

10. Теория вероятностей. Основные определения.

11. Классическое определение вероятности.

12. Геометрическое определение вероятности.

13. Теоремы сложения и умножения вероятностей.

14. Формула полной вероятности.

15. Схема независимых испытаний Бернулли.

16. Локальная и интегральная теоремы Муавра-Лапласа. Теорема Пуассона.

17. Случайные величины. Функция распределения.

18. Непрерывные случайные величины. Плотность вероятности.

19. Числовые характеристики случайных величин и их свойства.

20. Основные законы распределения дискретных случайных величин.

21. Основные законы распределения непрерывных случайных величин.

22. Системы двух случайных величин.

23. Закон больших чисел. Центральная предельная теорема и следствия из неё.

24. Математическая статистика. Основные определения.

25. Графические представления статистических рядов.

26. Точечные оценки параметров распределения.

27. Интервальные оценки параметров распределения.

28. Статистическая проверка статистических гипотез.

29. Критерий согласия Пирсона.

30. Основные понятия дисперсионного, корреляционного и регрессионного анализа. Метод наименьших квадратов.

1.Осн-ые задачи мат. прогр.

Если ф-ии,вход-ие в ф-лы будут линейны относ-но неизв-ых,то тк зад-а мат.прогр.наз-ся з-ей линейного прогр. Если,хотя бы одна 1 из ф-ий,вход-их в ф-лу нелинейна,то тк з-ча наз.з-ей нелинейного прогр.

Если все огр-ия,вх-ие в ф-ию а целевая ф-ия квадр-на отн-но пер-ых х1…хn,то тк з-ча наз.з-ей квадр-го прогр. Если все огр-ия лин-ны,а цел-ая ф-ия пр-ет из себя частное 2 линейных ф-ий,то тк з-ча наз.з-ей ровно лин-го прогр. Если на пер-ые х1,х2…хn или на их часть наложено условие целоч-ти,то тк з-ча наз.з-ей целочисл-го прогр. Если,хотя бы 1 коэф-ент в ф-ах зависит от 1 или неск-их парам-ов,то тк з-ча наз.з-ей параметр-го прогр. Если,хотя бы 1 из коэф-ов в ф-ах

явл.случ-ой вел-ой,то тк з-ча наз.з-ей стахостич-го прогр.

2.Лин-ое прогр.Формы ЗЛП

З-ча явл.з-ей лин-го прогр.и имеет н-ие з-ча лин-го прогр.в нормальной форме. З-ча наз.з-ей лин-го прогр.в кононичной форме.Мжн от общей з-чи перейти к з-че в конон-ой форме:

1)если целевая ф-ия рассм-ся на min,то,поставив перед цел-ой ф-ей зна«-»,перех-им к з-че на max;

2)если огр-ие в исх-ой з-че типа<или=,то вводя новую иск-ую неотр-ую перем-ую и приб-яя её к левой части огр-ия,пол-им огр-ие типа рав-ва,причем н-ые иск-ые огр-ия в цел-ую ф-ию не вх-ят;

3)если исх-ое огр-ие типа>либо=,то вводя новую неизв-ую неотр-ую перем-ую и отнимая ее от левой части огр-ия прих-ит огр-ие типа рав-ва;

4)если на к.-л. перем-ую из исх-ой з-чи хj0 не наложено усл-ие неотриц-ти,то заменим её разностью новых 2 неотр-ых перем-ых;

5)если в к.-л. огр-ии рав-ва исх-ой пр-ой части стоит вел-на,то умн-ив обе части на -1,придем к эквивал-му рав-ву,в правой части ктрг будет полож-ая вел-на.

Набор знач-ий перем-ых,ктр уд-ет всем огр-ям 2,3 з-ч мат.прогр.наз.планом з-чи мат.прогр.

3.Геом-ий метод реш-ия з-чи лин-го пр-ия

Если задача линейного программирования в стандартной форме содержит всего лишь две переменные x₁ и x₂ (т.е. n=2), то ее можно решить следующим способом, основанным на ее геометрической интерпретации. Каждое неравенство системы ограничений и условие неотрицательности представляют собой полуплоскость. Пересечение полуплоскостей образует выпуклое многоугольное множество (многогранник допустимых решений). Целевая функция графически изображается множеством параллельных прямых, называемых линиями уровня, каждой из которых соответствует конкретное значение z.Для решения задачи линия уровня сдвигается в пределах области допустимых решений (многогранника допустимых решений) в направлении вектора-градиента

grad z = f (x) = 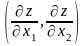до самой крайней точки области для задачи максимизации, и в направлении антиградиента – grad z=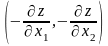 для задачи минимизации. Координаты этой точки и определяют решение ЗЛП (оптимальный план задачи).

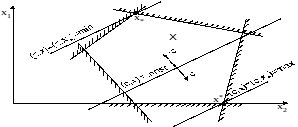
Рис1. Геометрическая интерпретация ЗЛП в стандартной форме

Рис.2 Пример пустой области допустимых решений (X)

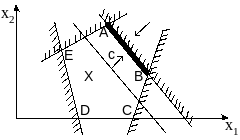
Рис.3 Пример ЗЛП, имеющий бесконечное множество решений (ребро АВ многогранника допустимых решений ABCDE)

4) Симплекс-метод решения злп в норм. Форме

симплекс-метод решения ЗЛП: идея метода и построение первоначального базисного плана. Симплексная таблица.

идея заключается в том, что, начиная с некоторого исходного невырожденного базисного плана , осуществляется последовательно направленное перемещение по опорным решениям задачи – вершинам ОДР к оптимальному плану. При этом значение целевой функции для задач на максимум не убывает. Через конечное число шагов получим оптимальное решение или установим неограниченность целевой функции на ОДР.

Допустим, имеется исходная ЗЛП в канонической форме:  F(X)=c₁X₁+c₂X₂+...+c_nX_n => max

a_1,1X₁+a_1,2X₂+...+a_1,nX_n=b₁ a_2,1X₁+a_2,2X₂+...+a_2,nX_n=b₂ a_m,1X₁+a_m,2X₂+...+a_m,nX_n=b_m

В общем случае m любых переменных можно выразить через оставшиеся (n-m) переменных, например - X₁...X_m через X_m+1...X_n: 

X₁=B₁-(A_1,m+1X_m+A_1,m+2X_m+2+...+A_1,nX_n) X_m=B_m-(A_m,m+1X_m+1+A_m,m+2X_m+2+...+A_m,nX_n)

Здесь коэфициенты В_i и А_i,j выражаются через b_i и a_i,j.  Переменные X₁... X_m называются базисными, а X_m+1...X_n- свободными.  Если положить X_m+1=...=X_n=0, то X_i=B_i и если при этом все B_i =0, то и X_i =0, и такой вектор:  X=(B₁, B₂, ..., B_m, 0, 0 ,..., 0)  называется базисным Выражение целевой функции через свободные переменные:  F=C₀-(C_m+1X_m+1+...+C_nX_n) Здесь коэффициенты C₀, C_m+1, ..., C_n выражаются через с_j, B_i, a_{i, j}. 

симплекс-метод решения ЗЛП: проверка плана на оптимальность.

Критерием оптимальности рассматриваемого плана является выполнение условия

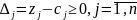
Возможны три случая:

1. Все оценки 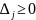тогда найденный базисный план оптимален.

2. Для некоторого j оценка 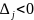и все элементы 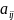соответствующего столбца 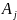неположительные,. В этом случае задача неразрешима, те целевая функция не ограничена на множестве допустимых планов(z стремится к бесконечности)

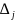3. Среди оценок есть отрицательные, причем для каждого номера j с в соответствующем столбце имеются положительные элементы . Тогда план не явл-ся оптимальным и следует искать новый базисный план, при котором значение целевой функции z было бы не меньше.

4. Выбрать свободную переменную, которую надо ввести в базис (выбор разрешающего столбца): это столбец, с минимальным значением С_j (пусть это k-й столбец)

5. Выбрать базисную переменную, которую надо вывести из базиса (выбор разрешающей строки): рассмотрим k-й столбец и все его элементы, которые больше нуля, т.е. A_i,k>0; для всех этих элементов находим отношение B_i/A_i,k и выбираем строку, которая соответствует минимальному значению этого отношения (пусть это i-я строка); соответствующая i-я переменная X_i выводится из базиса; при нескольких одинаковых отношениях берем любую строку; элемент A_i,k называется разрешающим элементом.

6.  Пересчитать симплекс-таблицу: составляем новую симплекс-таблицу заменив в составе базисных переменных X_i на X_k; заполняем сначала новую k-ю строку, записывая в нее элементы старой i-ой строки, поделенные на разрешающий элемент; после заполнения k-ой строки заполняем оставшиеся строки; для этого k-ю строку умножаем последовательно на такие числа, чтобы после сложения ее с каждой строкой старой таблицы в k-ом столбце получить везде ноль (кроме единицы в k-ой строке).