15.3. Частотная автоподстройка частоты

Звенья устройства. Структурная схема устройства ЧАП непрерывного типа соответствует схеме АПЧ (рис. 15.2).

В ней под звеном сравнения следует понимать частотный дискри­минатор, напряжение на выходе которого зависит от частоты на его входе. Известно несколько схем частотных дискриминаторов, наиболее распространенными из которых являются схемы балансного типа (рис. 15.4) и на расстроенных контурах.

Рис. 15.4. Частотный дискриминатор балансного типа

В качестве частотного дискриминатора может использоваться и микросхема, имеющая два входа (рис. 15.5, а). На 1-й вход подается сигнал частоты f₀, определяющий среднюю частоту дискриминатора, а на 2-й - сигнал разностной частоты f_р=f_ст–f_эт. При f_p>f₀ напряжение на выходе дискриминатора и_д=U_д, а при f_p<f₀ напряжение и_д=–U_д. В результате характеристика дискриминатора имеет вид, приведенный на рис. 15.5, б.

Р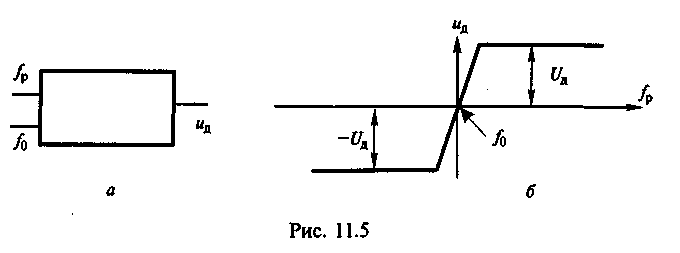 ис. 15.5. Характеристика дискриминатора

Из схем управления частотой автогенератора выделим две: с варикапом и ферритом. Варикапом называется полупроводниковый диод, емкость закрытого р-n-перехода которого существенно зависит от значения обратного напряжения U_обр. Данная зависимость определяется следующим примерным соотношением: . (15.1)

Схема управляющего элемента с варикапом приведена на рис. 15.6.

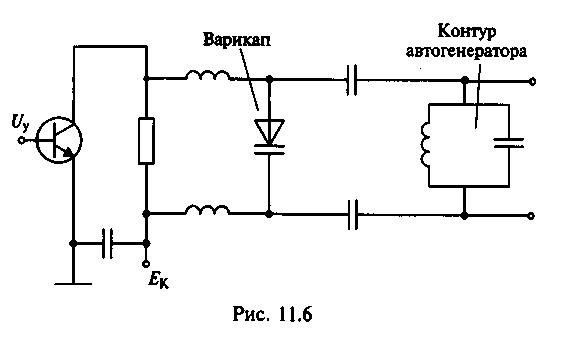
Рис. 15.6. Схема управляющего элемента с варикапом

Схема управляющего элемента с ферритом показана на рис. 15.7. Катушка индуктивности с ВЧ ферритом располагается в зазоре электромагнита. При изменении тока подмагничивания меняется дифференциальная магнитная проницаемость феррита, что приводит к измерению индуктивности контура и частоты автоколебаний.

Р ис. 15.7. Схема управляющего элемента с ферритом

В обеих схемах характеристика управляющего элемента f_y=(U_y) подобна характеристике, приведенной на рис. 15.3,б. В качестве ФНЧ может использоваться однозвенный RC-фильтр (рис. 15.8).

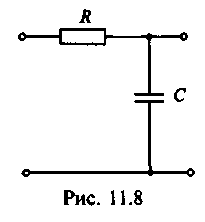
Рис. 15.8. Однозвенный RC-фильтр.

Определим точность ЧАП в установившемся режиме работы, в котором линейная модель устройства описывается системой из трех уравнений: (15.2)

где f_ст - отклонение частоты стабилизируемого автогенератора от номинального значения; f_н - начальная расстройка того же автогенератора; f_y - изменение частоты автогенератора под действием управляющего элемента в замкнутой системе. (Остальные параметры определены выше на рис. 15.3.). Решив совместно уравнения (15.2), получим уравнение для отклонения частоты стабилизируемого автогенератора в установившемся режиме работы: , (15.3)

где f_о.р. - остаточная расстройка.

И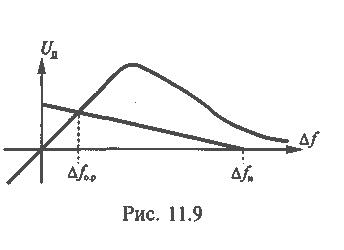 з (15.3) следует, что благодаря действию устройства ЧАП первоначальное отклонение частоты стабилизируемого автогенератора от номинального значения f_н уменьшается в К_рег=(1+S_уS_д) раз. Поскольку коэффициент авторегулирования К_рег>>1, то это уменьшение может быть весьма существенным - в 1000 и более раз. Графическое решение уравнений (15.2) представлено на рис. 15.9. Из него также следует, что решением уравнений (15.2) является величина f_ст=f_о.р.. Именно на эту величину, которая определяет точность ЧАП, отличается частота стабилизируемого автогенератора от номинального значения в установившемся режиме.

Рис. 15.9. Графическое решение уравнений (15.2)

Пример. Начальная расстройка f_н=000 кГц. Крутизна S_y=400 кГц/В, крутизна S_д=5 В/кГц. Коэффициент регулирования К_рег=1+S_уS_д=2001. Остаточная расстройка f_о.р.=f_н/К_рег=0,5 кГц. Таким образом, нестабильность частоты стабилизируемого автогенератора с 1000 кГц уменьшается до 500 Гц.