Лабораторная работа № 3 Определение географических и плоских прямоугольных координат

Цель работы׃ приобретение практических навыков в получении необходимых данных для построения рабочих планов и чертежей.

Место проведения работы: лаборатория инженерной геодезии учебного полигона.

Инструменты и принадлежности׃

- карта и план учебного полигона;

- геодезическая линейка;

- циркуль-измеритель;

- пятизначные таблицы.

Общие теоретические сведения

Для определения местонахождения точки на плане (карте) необходимо знать ее координаты. Координаты, в зависимости от вида выполняемой работы, делятся на географические (общее название астрономических и геодезических координат) и плоские прямоугольные координаты.

В авиации и судовождении используют географические координаты. При построении планов, выносе точек в натуру и др. используют плоские прямоугольные координаты Гаусса – Крюгера.

Для определения положения точек на сфере со времен Птолемея (ок. 150 г. н. э.) используются географические координаты: широта φ и долгота λ, отсчитываемые от плоскости земного экватора и нулевого меридиана.

Под плоскостью земного экватора понимают плоскость, проходящую через центр Земли перпендикулярно к ее оси вращения; под плоскостью географического (астрономического) меридиана – плоскость, проходящую через отвесную линию и ось вращения Земли или параллельно последней. Линии пересечения плоскостей географических меридианов с поверхностью эллипсоида называются меридианами. Линии, образованные при пересечении плоскостей, проходящих перпендикулярно к оси вращения Земли, с поверхностью эллипсоида, называются параллелями. Нулевым меридианом считается меридиан, проходящий через центр главного зала Гринвичской обсерватории, находящейся в окрестностях Лондона. Гринвичский меридиан принят основным (нулевым) меридианом на научной конференции географов и геодезистов в США в 1884 г.

Сеть меридианов и параллелей, нанесенных определенным образом на поверхность эллипсоида, представляют собой координатные оси географической системы координат. От них определяют широту и долготу.

Под долготой понимают двугранный угол между плоскостью Гринвичского (нулевого) меридиана и плоскостью данного меридиана (в нашем случае меридиана точки Р); под широтой – угол, составленный отвесной линией точки Р с плоскостью экватора (рис. 3.1,а). Широта обозначается буквой , а долгота - . Между внешней и внутренней рамками в нижнем левом углу трапеции карты даны широта и долгота в градусах, минутах и секундах (рис.1.1, 1.2).

Нарастание цифр идет с левого нижнего угла к левому верхнему (от экватора к северу – северная широта) и правому нижнему (с запада на восток или на запад от Гринвичского меридиана – западная или восточная долгота).

Рис. 3.1. Системы координат: а – географических; б – плоских прямоугольных

Например (рис.1.1), в нижнем левом углу слева карта имеет оцифровку по широте (меридиану) 53˚00΄, по долготе (параллели) 11˚52΄30΄΄, в верхнем углу (по меридиану)

- 53˚05΄, в правом нижнем углу (параллель) - 12˚00΄. Размер рамки по широте равен 53˚05΄− 53˚00΄=5΄, по долготе 12˚00΄ − 11˚52΄30΄΄=7΄30΄΄.

Минутный интервал выделяется попеременно черными и белыми шашечками. Минутный интервал (шашечки) разделен точками на секунды. Чтобы определить цену деления в секундах, необходимо , где n - количество точек на минутном интервале. Если минутный интервал не разделен на секунды, то можно определить цену деления по широте и долготе.

Цена деления по широте ЦД_φ= ,

а по долготе ЦД_λ= ,

где φ_max, φ_min – соответственно верхняя и нижняя надписи по широте, l_φ – длина рамки карты между и φ_max, φ_min, λ_max, λ_min- оцифровка карты по долготе; l_λ – длина рамки карты по долготе.

Например (рис.1.1), при длине рамки карты по широте, равном 40,5 см и долготе 38,2 см:

ЦД_φ = = =7,41΄΄.

ЦД _λ = =11΄΄,78.

Таким образом, по широте цена деления в 1см - 7΄΄,41, по долготе в 1см - 11΄΄,78.

Для определения географической широты (φ) и долготы (λ) необходимо из заданной точки опустить перпендикуляры на меридиан и параллель, взять отсчеты в градусах, минутах и секундах. Широта определяется по формуле:

φ_i = φ _нач ± ∆ φ; (3.1)

долгота: λ_i = λ _нач ± ∆ λ, (3.2)

где φ_нач, λ_нач – соответственно, значения начальной широты и долготы; Δφ, Δλ – расстояние от начальной оси до определяемой точки в угловых единицах. Если за начальную ось принят левый меридиан и нижняя параллель, то знак (+), если правый меридиан и верхняя параллель, то знак (-).

Например, на рис.1.1 для точки В:

широта φ_В= φ_нач+ Δφ =53º00´00´´+1´+8´´=53º01´08´´;

долгота λ_В= λ_нач+ Δλ= 11º52´30´´+30´´+54´´=11º53´54´´.

Для точки С:

широта φ_с = φ_нач – Δφ = 53˚05´-20´´=53°04´40´´;

долгота λ_с = λ_нач – Δλ =12˚00΄΄00΄΄=11˚59΄09΄΄.

На внешней стороне внутренней рамки по широте также даны абсциссы горизонтальной линии в километрах (например, рис.1.1 для первой линии 5879 км, второй, третьей и т.д. 5880, 5881 и т.д. километров от экватора). Цифра 60 не повторяется. Полная надпись 5879, 5880, 5881 и т.д. По горизонтали даны ординаты линий сетки – 2694, 95… 2700, 01 и т.д. или полная надпись 2694, 2695,…, 2700, 2701…, где 2 – номер зоны, а 694, 695,…, 700, 701 и т.д. - значения ординаты в километрах от осевого меридиана (рис.1.1).

Долгота осевого меридиана равна 6N-3, где N – номер зоны. Размер зоны в градусах - 6˚, в километрах - . Начало зоны определяется как 6˚ (N-1), а ее конец - 6˚N.

Зона осевым меридианом делится на 2 части: на запад ординаты отрицательные, на восток – положительные.

Чтобы избежать отрицательных значений ординат, ось абсцисс (х) условно перенесли на 500 км к западу от осевого меридиана. Исправленную таким образом ординату называют приведенной (х˚).

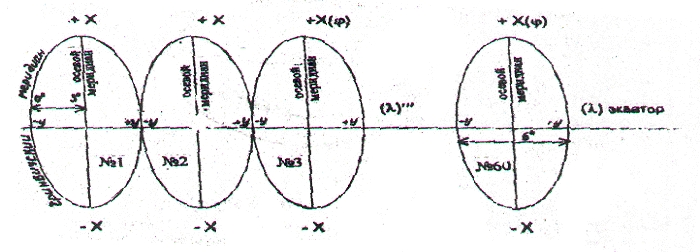
Рис.3.2. Зональная система прямоугольных координат.

Координата X = Х_нач ±ΔХ; Y=Y_нач ±ΔY, (3.3)

где Х,Y – координаты определяемой точки; Х_нач, Y_нач – координаты оси принятой за начальную. Знак (+) или (-) применяется в зависимости от положения начальной оси. Если ось координат ниже и левее определяемой точки, то знак (+), в противном случае знак (-).

В свою очередь ∆X=l_X M, ∆Y=l_Y M,

где l_х, l_Y – расстояние в см от точки до ближайшей оси линии сетки x,y; M – знаменатель масштаба. Например (рис. 1.1), для точки B знаменатель масштаба равен 25000 см или 250 м:

Х^нач=5880, ∆X=3,03 250=757,50 м или 0,757 км. В этом случае׃

Х=5880+0,757=5880,757 км от экватора.

Y_нач=694, ∆Y=1,84 250=460 м или 0,46 км.

Приведенная ордината Y=694+0,46=694,46 км.

Для определения абсолютного значения ординаты от полученного значения необходимо вычесть 500 км. В этом случае Y=694,46-500=194,46 км, т.е. точка расположена к востоку от осевого меридиана.

Если для точки B (рис.1.1) за начальные оси принять линию со значением 5881 и 2695, тогда

Х = Х_нач - ∆X; Y = Y_нач - ∆Y – 500 км;

Х=5881- ∆X; Y=2695 - ∆Y-500 км.