----------------------------------------------------------------------1-----------------------------------------------------------------------

" Предмет и основные понятия информатики"

Информатика - это комплексная, техническая наука, которая систематизирует приемы создания, сохранения, воспроизведения, обработки и передачи данных средствами вычислительной техники, а также принципы функционирования этих средств и методы управления ими. Термин "информатика" происходит от французского слова Informatique и образован из двух слов: информация и автоматика. Этот термин введен во Франции в середине 60-х лет XX ст., когда началось широкое использование вычислительной техники. Тогда в англоязычных странах вошел в употребление термин "Computer Science" для обозначения науки о преобразовании информации, которая базируется на использовании вычислительной техники. Теперь эти термины являются синонимами.

Появление информатики обусловлено возникновением и распространением новой технологии сбора, обработки и передачи информации, связанной с фиксацией данных на машинных носителях.

Предмет информатики как науки составляют:

• аппаратное обеспечение средств вычислительной техники;

• программное обеспечение средств вычислительной техники;

• средства взаимодействия аппаратного и программного обеспечения;

• средства взаимодействия человека с аппаратными и программными средствами.

Средства взаимодействия в информатике принято называть интерфейсом. Поэтому средства взаимодействия аппаратного и программного обеспечения иногда называют также программно-аппаратным интерфейсом, а средства взаимодействия человека с аппаратными и программными средствами - интерфейсом пользователя.

Основной задачей информатики как науки - это систематизация приемов и методов работы с аппаратными и программными средствами вычислительной техники. Цель систематизации состоит в том, чтобы выделять, внедрять и развивать передовые, более эффективные технологии автоматизации этапов работы с данными, а также методически обеспечивать новые технологические исследования.

Информатика - практическая наука. Ее достижения должны проходить проверку на практике и приниматься в тех случаях, если они отвечают критерию повышения эффективности. В составе основной задачи сегодня можно выделить такие основные направления информатики для практического применения :

• архитектура вычислительных систем (приемы и методы построения систем, предназначенных для автоматической обработки данных);

• интерфейсы вычислительных систем (приемы и методы управления аппаратным и программным обеспечением);

• программирование (приемы, методы и средства разработки комплексных задач); преобразование данных (приемы и методы преобразования структур данных);

• защита информации (обобщение приемов, разработка методов и средств защиты данных);

• автоматизация (функционирование программно-аппаратных средств без участия человека);

• стандартизация (обеспечение совместимости между аппаратными и программными средствами, между форматами представления данных, относящихся к разным типам вычислительных систем).

На всех этапах технического обеспечения информационных процессов для информатики ключевым вопросом есть эффективность. Для аппаратных средств под эффективностью понимают соотношение производительности оснащение к его стоимости. Для программного обеспечения под эффективностью принято понимать производительность работающих с ним пользователей. В программировании под эффективностью понимают объем программного кода, созданного программистами за единицу времени. В информатике всю жестко ориентированное на эффективность. Вопрос как осуществить ту или другую операцию, для информатики важный, но не основной. Основным есть вопрос как совершить данную операцию эффективно.

В рамках информатики, как технической науки можно сформулировать понятия информации, информационной системы и информационной технологии.

----------------------------------------------------------------------2-----------------------------------------------------------------------

Информация

Информация - это совокупность сведений (данных), которая воспринимается из окружающей среды (входная информация), выдается в окружающую среду (исходная информация) или сохраняется внутри определенной системы.

Информация существует в виде документов, чертежей, рисунков, текстов, звуковых и световых сигналов, электрических и нервных импульсов и т.п..

Важнейшие свойства информации:

• объективность и субъективность;

• полнота;

• достоверность;

• адекватность;

• доступность;

• актуальность.

Данные являются составной частью информации, представляющие собой зарегистрированные сигналы.

Во время информационного процесса данные преобразовываются из одного вида в другого с помощью методов. Обработка данных включает в себя множество разных операций. Основными операциями есть:

• сбор данных - накопление информации с целью обеспечения достаточной полноты для принятия решения;

• формализация данных - приведение данных, которые поступают из разных источников к единой форме;

• фильтрация данных - устранение лишних данных, которые не нужны для принятия решений;

• сортировка данных - приведение в порядок данных за заданным признаком с целью удобства использования;

• архивация данных - сохранение данных в удобной и доступной форме;

• защита данных - комплекс мер, направленных на предотвращение потерь, воспроизведения и модификации данных;

• транспортирование данных - прием и передача данных между отдаленными пользователями информационного процесса. Источник данных принят называть сервером, а потребителя - клиентом;

• преобразование данных - преобразование данных с одной формы в другую, или с одной структуры в другую, или изменение типа носителя.

Объективность и субъективность информации. Понятие объективности информации является относительным. Это понятно, если учесть, что методы являются субъективными. Более объективной принято считать ту информацию, в которую методы вносят меньший субъективный элемент. Так, например, принято считать, что в результате наблюдения фотоснимка природного объекта или явления образуется более объективная информация, чем в результате наблюдения рисунка того же объекта, выполненного человеком. В ходе информационного процесса степень объективности информации всегда понижается. Это свойство учитывают, например, в правовых дисциплинах, где по-разному обрабатываются показания лиц, непосредственно наблюдавших события или получивших информацию косвенным путем (посредством умозаключений или со слов третьих лиц). В не меньшей степени объективность информации учитывают в исторических дисциплинах. Одни и те же события, зафиксированные в исторических документах разных стран и народов, выглядят совершенно по-разному. У историков имеются свои методы для тестирования объективности исторических данных и создания новых, более достоверных данных путем сопоставления, фильтрации и селекции исходных данных. Обратим внимание на то, что здесь речь идет не о повышении объективности данных, а о повышении их достоверности (это совсем другое свойство).

Полнота информации. Полнота информации во многом характеризует качество информации и определяет достаточность данных для принятия решений или для создания новых данных на основе имеющихся. Чем полнее данные, тем шире диапазон методов, которые можно использовать, тем проще подобрать метод, вносящий минимум погрешностей в ход информационного процесса.

Достоверность информации. Данные возникают в момент регистрации сигналов, но не все сигналы являются «полезными» — всегда присутствует какой-то уровень посторонних сигналов, в результате чего полезные данные сопровождаются определенным уровнем «информационного шума». Если полезный сигнал зарегистрирован более четко, чем посторонние сигналы, достоверность информации может быть более высокой. При увеличении уровня шумов достоверность информации снижается. В этом случае для передачи того же количества информации требуется использовать либо большие данных, либо более сложные методы.

Адекватность информации — это степень соответствия реальному объективному состоянию дела. Неадекватная информация может образовываться при создании новой информации на основе неполных или недостоверных данных. Однако и полные, и достоверные данные могут приводить к созданию неадекватной информации в случае применения к ним неадекватных методов.

Доступность информации — мера возможности получить ту или иную информацию. На степень доступности информации влияют одновременно как доступность данных, так и доступность адекватных методов для их интерпретации. Отсутствие доступа к данным или отсутствие адекватных методов обработки данных приводят к одинаковому результату: информация оказывается недоступной. Отсутствие адекватных методов для работы с данными во многих случаях приводит к применению неадекватных методов, в результате чего образуется неполная, неадекватная или недостоверная информация.

Актуальность информации — это степень соответствия информации текущему моменту времени. Нередко с актуальностью, как и с полнотой, связывают коммерческую ценность информации. Поскольку информационные процессы растянуты во времени, то достоверная и адекватная, но устаревшая информация может приводить к ошибочным решениям. Необходимость поиска (или разработки) адекватного метода для работы с данными может приводить к такой задержке в полз^ении информации, что она становится неактуальной и ненужной. На этом, в частности, основаны многие современные системы шифрования данных с открытым ключом. Лица, не владеющие ключом (методом) для чтения данных, могут заняться поиском ключа, поскольку алгоритм его работы доступен, но продолжительность этого поиска столь велика, что за время работы информация теряет актуальность и, соответственно, связанную с ней практическую ценность.

----------------------------------------------------------------------3-4--------------------------------------------------------------------

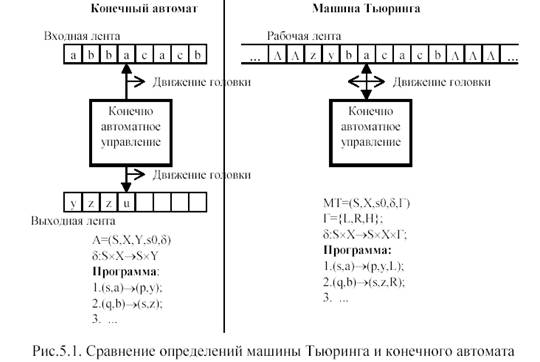
Рассмотрим, чем отличается машина Тьюринга от простой модели конечного автомата. Конечный автомат можно представить себе как устройство с конечным числом внутренних состояний, работающее с двумя лентами: входной и выходной (рис.5.1). Конечный автомат работает по тактам. На каждом такте он читает с помощью некоторой входной головки символ из обозреваемой ячейки входной ленты, изменяет свое состояние и печатает некоторый символ выходного алфавита в обозреваемую ячейку выходной ленты, после чего две его головки чтения и записи перемещаются на одну позицию вправо. Описание функционирования конечного автомата можно считать его программой: в ней просто перечислено конечное число четверок (команд) <s,a,p,y)>, где s – текущее состояние, a - очередной входной сигнал, р - следующее состояние и у - очередной выходной сигнал.

Программа КА - это просто перечисление аргументов и соответствующих результатов частично-определенной функции переходов и выходов автомата .:S.X>S.Y. В своем вычислительном устройстве Тьюринг просто смоделировал доведенный до самых элементарных операций процесс выполнения произвольного алгоритма человеком. Человек имеет конечную память, и в этом смысле его можно представить системой с конечным числом состояний. Исходная информация к алгоритму обычно представляется в виде цепочки символов. Можно себе представить, что эта информация представлена в виде слова (конечной последовательности символов) конечного словаря. Выполняя алгоритм, человек-вычислитель использует дополнительную память (которая может быть потенциально бесконечной, например, листы бумаги) для записи информации, причем эта запись производится им последовательно, символ за символом. При вычислениях человек может возвращаться к ранее записанной информации, стирать некоторую информацию и т.д. Таким образом, элементарными операциями при выполнении алгоритма можно считать запись и стирание символа, а также перенесение внимания с одного участка записи на другой. Предложенная Тьюрингом формальная модель отличается от конечного автомата только в этих двух аспектах: она имеет одну бесконечную рабочую ленту, с которой читает и куда пишет символы, и одну головку чтения-записи, которая может двигаться по рабочей ленте в любую сторону (рис.5.1). Такая свобода движения головки чтения-записи по сути означает возможность создавать и впоследствии анализировать промежуточную информацию. Как оказывается, такое простое расширение возможностей радикально увеличивает вычислительную мощность машин Тьюринга по сравнению с обычными конечными автоматами.

Машина Тьюринга работает по тактам. На каждом такте она читает символ из обозреваемой ячейки рабочей ленты, изменяет свое состояние в зависимости от своего внутреннего состояния и прочитанного символа и печатает символ в обозреваемую ячейку рабочей ленты, после чего ее головка чтения-записи может переместиться на одну позицию влево, вправо или остается на месте. Описание функционирования МТ можно считать ее программой, которая представлена конечным набором пятерок (команд) < s,a,p,y,D >, где s, a, р и у имеют тот же смысл, что и в конечном автомате, а D -направление перемещения головки по рабочей ленте, которое может быть одним из трех значений: L -влево, R - вправо и Н - оставаться на месте. Иными словами, программа МТ- это просто конечный список пятерок, представляющих собой аргументы и соответствующие им результаты частично-определенной функции переходов и выходов .:S.X>S.X.Г.

Машина Тьюринга имеет один конечный рабочий алфавит X, в котором входные и выходные символы не различаются: выходной символ, напечатанный на ленте, машина может прочитать в последующих тактах. Для удобства обычно считают, что X содержит пустой символ ., находящийся во всех ячейках рабочей ленты слева и справа от конечной цепочки “значащих” символов в начале работы.

Рассмотрим, как работает машина Тьюринга. Конфигурацией машины Тьюринга называется ее текущее состояние, текущее состояние рабочей ленты и место расположения головки. При работе МТ в каждом такте происходит смена конфигураций. Пусть МТ находится в состоянии s и в обозреваемой ячейке ленты находится символ a. Если в программе МТ нет команды для пары <s,a>, то МТ останавливается. Если в программе МТ несколько команд для данной пары <s,a>, то это - недетерминированная машина Тьюринга, в ней выполняется одна из нескольких возможных команд с левой частью <s,a>. Очевидно, что в любой момент работы на ленте МТ находится только конечная цепочка “значащих” символов. После останова машины Тьюринга эта цепочка является результатом переработки входной цепочки. Таким образом, МТ является автоматом-преобразователем символьных цепочек.

Машина Тьюринга также может быть распознавателем множеств цепочек. В такой МТ выделяются специальные заключительные состояния стоп или “!”, и если МТ, работающая как распознаватель, останавливается в одном из этих состояний при пустой входной ленте, то она распознает входную цепочку. Если в заключительном состоянии останавливается машина-преобразователь Тьюринга, то информация на рабочей ленте является результатом переработки входной информации.

Alt

Машина Тьюринга состоит из трех частей: ленты, считывающе-записывающей головки и логического устройства Лента выступает в качестве внешней памяти; она считается неограниченной (бесконечной) – уже это свидетельствует о том, что машина Тьюринга является модельным устройством, поскольку ни одно реальное устройство не может обладать памятью бесконечного размера.

Лента разбита на отдельные ячейки, однако, в машине Тьюринга неподвижной является головка, а лента передвигается относительно нее вправо или влево. Другим отличием является то, что она работает не в двоичном, а некотором произвольном конечном алфавите A = { , a1…a n} – этот алфавит называется внешним. В нем выделяется специальный символ – , называемый пустым знаком – его посылка в какую-либо ячейку стирает тот знак, который до этого там находился, и оставляет ячейку пустой. В каждую ячейку ленты может быть записан лишь один символ. Информация, хранящаяся на ленте, изображается конечной последовательностью знаков внешнего алфавита, отличных от пустого знака.

Таким образом, в машине Тьюринга реализуется система предельно простых команд обработки информации. Эта система команд обработки дополняется также предельно простой системой команд перемещений ленты: на ячейку влево, на ячейку вправо и остаться на месте, т.е. адрес обозреваемой ячейки в результате выполнения команды может либо измениться на 1, либо остаться неизменным. Однако, хотя фактически происходит перемещение ленты, обычно рассматривается сдвиг головки относительно обозреваемой секции – по этой причине команда сдвига ленты влево обозначается R («Right»), сдвига вправо – L («Left»), отсутствие сдвига – S («Stop»).

Обработка информации и выдача команд на запись знака, а также сдвига ленты в машине Тьюринга производится логическим устройством (ЛУ). ЛУ может находиться в одном из состояний, которые образуют конечное множество и обозначаются Q ={q1…qm, z} , причем, состояние z соответствует завершению работы, а q1 является начальным (исходным). Q совместно со знаками R, L, S образуют внутренний алфавит машины. ЛУ имеет два входных канала (ai, qi) и три выходных (ai+1, qi+1, Di+1)

----------------------------------------------------------------------5-----------------------------------------------------------------------

Конечные автоматы

Автомат – устройство, которое без непосредственного участия человека выполняет обработку информации по заложенной в него программе. В информатике автомат – дискретный преобразователь информации, который преобразует некоторое множество входных сигналов в выходные, проходя при этом через множество состояний. Если указанные множества конечны, то автомат называется конечным. Теория автоматов занимается изучением абстрактных вычислительных устройств. Конечные автоматы являются моделями для многих компонентов аппаратного и программного обеспечения. С точки зрения теории, конечный автомат может рассматриваться как частный случай формально заданного алгоритма, поэтом теория конечных автоматов имеет отношение к теории алгоритмов. Конечные автоматы удобно представлять в виде ориентированного графа, у которого вершины обозначают состояния, а ребра определяют переходы из одного состояния в другое под действием соответствующих входных сигналов. На этих же ребрах указывают выходы. Автомат можно представлять таблично, задавая функции переходов и выходов. Сама реализация конечного автомата может быть программной (представленной в виде блок-схемы или на одном из языков программирования) и аппаратной, для которой предварительно используется двоичное кодирование. Два конечных автомата эквивалентны, если реализуемые ими отображения вход-выход эквивалентны. ^ Функции автомата определены на всех входных сигналах, а расширенные функции переходов и выходов - на множестве входных цепочек (цепочка – последовательность символов некоторого алфавита). Состояние автомата называют недостижимым, если не существует пути из начального состояния, в противном случае состояние автомата – достижимое. Состояние конечного автомата называется достижимым, если существует такая цепочка, под воздействием которой автомат попадает в такое состояние. Конечные автоматы называются эквивалентными, если выполнены два условия:

1. их входные алфавиты совпадают;

2. реализуемые ими отображения совпадают.

Произведение автоматов – это два стоящих рядом невзаимодействующих конечных автомата, синхронно работающих на одном входе. Минимизацией конечного автомата называют задачу нахождения минимального автомат, который реализует заданное автоматное отображение.

Типы конечных автоматов

По способу формирования функций выхода выделяют автоматы Мили и Мура.

В автомате Мили функция выходов  определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель автомата Мили и схема рекуррентных соотношений не отличаются от математической модели и схемы рекуррентных соотношений абстрактного автомата, т.е.

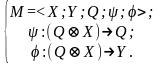(1.12)

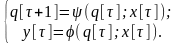(1.13)

Особенностью автомата Мили является то, что функция выходов является двухаргументной и символ в выходном канале y[] обнаруживается только при наличии символа во входном канале x[]. Функциональная схема не отличается от схемы абстрактного автомата (см. рис 1.2 и 1.3).

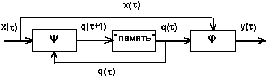
Рис. 1.3. Функциональная схема автомата Мили.

В автомате Мура функция  определяет значение выходного символа только по одному аргументу - состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе. Математическая модель и схема рекуррентных соотношений автомата Мура имеют вид:

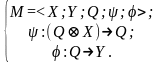(1.14)

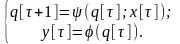(1.15)

Особенностью автомата Мура является то, что символ y[] в выходном канале существует все время пока автомат находится в состоянии q[]. Функциональная схема автомата Мура представлена на рис. 1.4.

Рис. 1.4. Функциональная схема автомата Мура.

Объединение автоматов Мили и Мура представляет С-автомат, для которого схема рекуррентных соотношений имеет вид:

(1.16)

Потребность такого автомата возникает при формировании автоматных сетей (см. 2).

Функциональная схема С-автомата представлена на рис.1. 5.

Рис.1. 5. Функциональная схема С-автомата.

Интересно выделить особые классы автоматов, математические модели которых опираются только на два носителя алгебры.

Пусть X=. Тогда математическая модель и система рекуррентных соотношений имеют вид:

(1.17)

(1.18)

Функциональная схема автомата приведена на рис.1.6.

Рис.1.6. Функциональная схема порождающего автомата.

Особенностью функционирования такого автомата является генерация последовательности символов выходного слова только в зависимости от последовательности состояний автомата. Такие автоматы называют порождающими или автономными. С помощью такого автомата генерируется последовательность управляющих команд на какие-либо объекты внешней среды.

Пусть Y=. Тогда математическая модель и система рекуррентных соотношений имеют вид:

(1.19)

q[1] = (q[];x[]); (1.20)

Функциональная схема автомата приведена на рис.1.7.

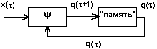
Рис. 1.7. Функциональная схема распознающего автомата.

Особенностью функционирования такого автомата является распознавание в последовательности изменений аргумента функции переходов значения (q_i[];x_i[]) и перевод автомата в заключительное состояние q_k. С помощью такого автомата обнаруживают заданные возмущения со стороны объектов внешней среды или распознают заданную последовательность входных символов. Поэтому такие автоматы называют распознающими. Часто и автомат Мура представляют автоматом без выхода, так как его выходной сигнал эквивалентен состоянию автомата.

Пусть Q=. Тогда математическая модель и система рекуррентных соотношений имеют вид:

(1.21)

y[] = (x[]); (1.22)

Функциональная схема автомата приведена на рис.8.

Рис. 1.8. Функциональная схема комбинационного автомата.

Особенностью функционирования такого автомата является отсутствие "памяти", т.е. на каждый символ входного алфавита автомат генерирует символ выходного алфавита без учета состояния автомата. Такие автоматы чаще всего называют комбинационными автоматами.

Автоматы удобно описывать с помощью таблиц, а для наглядности использовать графы. При табличном описании задают две таблицы, одна из которых раскрывает функцию переходов QX)Q (см. таблицу 1.1), а другая - функцию выходов QX)Y (см. таблицу 1.2). Число строк таблиц m равно числу состояний автомата, т.е. m = Q . Число столбцов таблиц n равно числу символов входного алфавита, т.е. n = X . В позиции первой таблицы записывают значения очередных состояний автомата q[1]Q, в которые он переходит для каждой пары (q[];x[])QX). В позиции второй таблицы записывают значения символов выходного алфавита y[]Y, которые генерирует автомат для каждой пары (q[];x[])QX). Если в таблицах 1 и 2 определены значения q[1]Q и y[]Y для каждой пары (q[];x[])QX), то есть заполнены все позиции таблиц, то дано описание детерминированного автомата.

----------------------------------------------------------------------6-----------------------------------------------------------------------

Электронная вычислительная машина, компьютер – комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач.

Классификация ЭВМ по принципу действия:

По принципу действия вычислительные машины делятся на три больших класса: аналоговые (АВМ), цифровые (ЦВМ) и гибридные (ГВМ).

Критерием деления вычислительных машин на эти три класса является форма представления информации, с которой они работают:

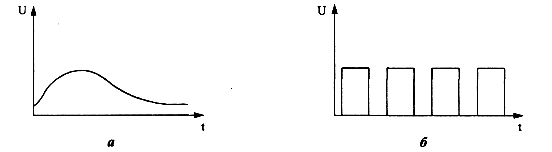
Две формы представления информации в машинах: а – аналоговая; б – цифровая.

Цифровые вычислительные машины (ЦВМ) – вычислительные машины дискретного действия, работают с информацией, представленной в дискретной, а точнее, в цифровой форме. Наиболее широкое применение получили ЦВМ с электрическим представлением дискретной информации – электронные цифровые вычислительные машины, обычно называемые просто электронными вычислительными машинами (ЭВМ), без упоминания об их цифровом характере.

Аналоговые вычислительные машины (АВМ) – вычислительные машины непрерывного действия, работают с информацией, представленной в непрерывной (аналоговой) форме, т.е. в виде непрерывного ряда значений какой-либо физической величины (чаще всего электрического напряжения). Аналоговые вычислительные машины весьма просты и удобны в эксплуатации; программирование задач для решения на них, как правило, нетрудоемкое; скорость решения задач изменяется по желанию оператора и может быть сделана сколь угодно большой (больше, чем у ЦВМ), но точность решения задач очень низкая (относительная погрешность 2-5 %). На АВМ наиболее эффективно решать математические задачи, содержащие дифференциальные уравнения, не требующие сложной логики.

Гибридные вычислительные машины (ГВМ) – вычислительные машины комбинированного действия, работают с информацией, представленной и в цифровой, и в аналоговой форме; они совмещают в себе достоинства АВМ и ЦВМ. ГВМ целесообразно использовать для решения задач управления сложными быстродействующими техническими комплексами.

Классификация ЭВМ по этапам создания:

По назначению ЭВМ можно разделить на три группы: универсальные (общего назначения), проблемно-ориентированные и специализированные.

Универсальные ЭВМ предназначены для решения самых различных инженерно-технических задач: экономических, математических, информационных и других задач, отличающихся сложностью алгоритмов и большим объемом обрабатываемых данных. Они широко используются в вычислительных центрах коллективного пользования и в других мощных вычислительных комплексах.

Характерными чертами универсальных ЭВМ являются: ? высокая производительность; ? разнообразие форм обрабатываемых данных: двоичных, десятичных, символьных, при большом диапазоне их изменения и высокой точности их представления; ? обширная номенклатура выполняемых операций, как арифметических, логических, так и специальных; ? большая емкость оперативной памяти; ? развитая организация системы ввода-вывода информации, обеспечивающая подключение разнообразных видов внешних устройств.

Проблемно-ориентированные ЭВМ служат для решения более узкого круга задач, связанных, как правило, с управлением технологическими объектами; регистрацией, накоплением и обработкой относительно небольших объемов данных; выполнением расчетов по относительно несложным алгоритмам; они обладают ограниченными по сравнению с универсальными ЭВМ аппаратными и программными ресурсами. К проблемно-ориентированным ЭВМ можно отнести, в частности, всевозможные управляющие вычислительные комплексы.

Специализированные ЭВМ используются для решения узкого круга задач или реализации строго определенной группы функций. Такая узкая ориентация ЭВМ позволяет четко специализировать их структуру, существенно снизить их сложность и стоимость при сохранении высокой производительности и надежности их работы. К специализированным ЭВМ можно отнести, например, программируемые микропроцессоры специального назначения; адаптеры и контроллеры, выполняющие логические функции управления отдельными несложными техническими устройствами, агрегатами и процессами; устройства согласования и сопряжения работы узлов вычислительных систем.

Классификация ЭВМ по размерам и функциональным возможностям:

По размерам и функциональным возможностям ЭВМ можно разделить на сверхбольшие (суперЭВМ), большие, малые, сверхмалые (микроЭВМ).

Исторически первыми появились большие ЭВМ, элементная база которых прошла путь от электронных ламп до интегральных схем со сверхвысокой степенью интеграции. Производительность больших ЭВМ оказалась недостаточной для ряда задач: прогнозирования метеообстановки, управления сложными оборонными комплексами, моделирования экологических систем и др. Это явилось предпосылкой для разработки и создания суперЭВМ, самых мощных вычислительных систем, интенсивно развивающихся и в настоящее время.

Появление в 70-х гг. малых ЭВМ обусловлено, с одной стороны, прогрессом в области электронной элементной базы, а с другой – избыточностью ресурсов больших ЭВМ для ряда приложений. Малые ЭВМ используются чаще всего для управления технологическими процессами. Они более компактны и значительно дешевле больших ЭВМ.

Дальнейшие успехи в области элементной базы и архитектурных решений привели к возникновению супермини-ЭВМ – вычислительной машины, относящейся по архитектуре, размерам и стоимости к классу малых ЭВМ, но по производительности сравнимой с большой ЭВМ.

Изобретение в 1969 г. микропроцессора (МП) привело к появлению в 70-х гг. еще одного класса ЭВМ – микроЭВМ. Именно наличие МП служило первоначально определяющим признаком микроЭВМ. Сейчас микропроцессоры используются во всех без исключения классах ЭВМ. Многопользовательские микроЭВМ – это мощные микроЭВМ, оборудованные несколькими видеотерминалами и функционирующие в режиме разделения времени, что позволяет эффективно работать на них сразу нескольким пользователям. Персональные компьютеры (ПК) – однопользовательские микроЭВМ, удовлетворяющие требованиям общедоступности и универсальности применения. Рабочие станции (work station) представляют собой однопользовательские мощные микроЭВМ, специализированные для выполнения определенного вида работ (графических, инженерных, издательских и др.). Серверы (server) – многопользовательские мощные микроЭВМ в вычислительных сетях, выделенные для обработки запросов от всех станций сети.

----------------------------------------------------------------------7-----------------------------------------------------------------------

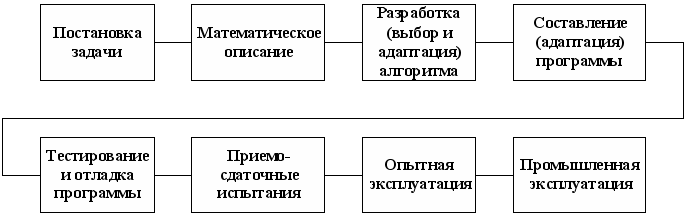Рис.7.1 - Этапы разработки программного обеспечения.

Первый этап представляет собой постановку задачи. На этом этапе раскрывается сущность задачи, т.е. формулируется цель ее решения; определяется взаимосвязь с другими задачами; указывается периодичность решения; устанавливаются состав и формы представления входной, промежуточной и результатной информации. Особое внимание в процессе постановки задачи уделяется детальному описанию входной, выходной (результатной) и межуточной информации. Особенность реализации этого этапа технологического процесса заключается в том, что конечный пользователь разрабатываемой программы, хорошо знающий ее проблемную сторону, обычно хуже представляет специфику и возможности использования ЭВМ для решения задачи. В свою очередь, предметная область пользователя (особенно ее отдельные нюансы, способные оказать влияние на решение задачи) зачастую незнакома разработчику программы, хотя он знает возможности и ограничения на применение ЭВМ. Именно эти противоречия являются основной причиной возникновения ошибок при реализации данного этапа технологического процесса разработки программ, которые затем неизбежно отражаются и на последующих этапах. Отсюда вся важность и ответственность этого этапа, требующего осуществления корректной и полной постановки задачи, а также необходимости однозначного ее понимания как разработчиком программы, так и ее пользователем. ^ Второй этап в технологии разработки программ - математическое описание задачи и выбор метода ее решения. Наличие этого этапа обусловливается рядом причин, одна из которых вытекает из свойства неоднозначности естественного языка, на котором описывается постановка задачи. В связи с этим на нем выполняется формализованное описание задачи, т.е. устанавливаются и формулируются средствами языка математики логико-математические зависимости между исходными и результатными данными. Математическое описание задачи обеспечивает ее однозначное понимание пользователем и разработчиком программы. Сложность и ответственность этапа математического описания задачи и выбора (разработки) соответствующего метода ее решения часто требуют привлечения квалифицированных специалистов области прикладной математики, обладающих знанием таких дисциплин, как исследование операций, математическая статистика, вычислительная математика и т.п. ^ Третий этап технологического процесса подготовки решения задач ЭВМ представляет собой алгоритмизацию ее решения, т.е. разработку оригинального или адаптацию (уточнение и корректировку) уже известного алгоритма.

Алгоритмизация - это сложный творческий процесс. В основу процесса алгоритмизации положено фундаментальное понятие математики и программирования - алгоритм. Алгоритм - это конечный набор правил, однозначно раскрывающих содержание и последовательность выполнения операций для систематического решения определенного класса задач за конечное число шагов. Любой алгоритм обладает следующими важными свойствами: Детерминированностью, массовостью, результатностью и дискретностью. Детерминированность алгоритма (определенность, однозначность) - свойство, определяющее однозначность результата работы алгоритма при одних и тех же исходных данных. Это означает, что набор указаний алгоритма должен быть однозначно и точно понят любым исполнителем. Массовость алгоритма - свойство, определяющее пригодность использования алгоритма для решения множества задач данного класса. Оно предполагает возможность варьирования исходными данными в определенных пределах. Свойство массовости алгоритма является определяющим фактором, обеспечивающим экономическую эффективность решения задач на ЭВМ, так как для задач, решение которых осуществляется один раз, целесообразность использования ЭВМ, как правило, диктуется внеэкономическими категориями.

Результатность алгоритма - свойство, означающее, что для любых допустимых исходных данных он должен через конечное число шагов (или итераций) завершить работу. Дискретность алгоритма - свойство, означающее возможность разбиения определенного алгоритмического процесса на отдельные элементарные действия. Таким образом, алгоритм дает возможность чисто механически решать любую задачу из некоторого класса однотипных задач. Составление (адаптация) программ (кодирование) является завершающим этапом технологического процесса разработки программных средств. Он предшествует началу непосредственно машинной реализации алгоритма решения задачи. Процесс кодирования заключается в переводе описания алгоритма на один из доступных для ЭВМ языков программирования. В процессе составления программы для ЭВМ конкретизируются тип и структура используемых данных, а последовательность действий, реализующих алгоритм, отражается посредством конкретного языка программирования. Этап тестирования и отладки. Оба эти процесса функционально связаны между собой, хотя их цели несколько отличаются друг от друга. Тестирование представляет собой совокупность действий, назначенных для демонстрации правильности работы программы в заданных диапазонах изменения внешних условий и режимов эксплуатации программы. Цель тестирования заключается в демонстрации отсутствия (или выявлении) ошибок в разработанных программах на заранее подготовленном наборе контрольных примеров.

----------------------------------------------------------------------8-----------------------------------------------------------------------

Аналоговая вычислительная машина (АВМ) — вычислительная машина, в которой каждому мгновенному значению переменной величины, участвующей в исходных соотношениях, ставится в соответствие мгновенное значение другой (машинной) величины, часто отличающейся от исходной физической природой и масштабным коэффициентом. Каждой элементарной математической операции над машинными величинами, как правило, соответствует некоторый физический закон, устанавливающий математические зависимости между физическими величинами на выходе и входе решающего элемента (например, законы Ома и Кирхгофа для электрических цепей, выражение для эффекта Холла, лоренцовой силы и т. д.).

В АВМ все математические величины представляются как непрерывные значения каких-либо физических величин. Главным образом, в качестве машинной переменной выступает напряжение электрической цепи. Их изменения происходят по тем же законам, что и изменения заданных функций. В этих машинах используется метод математического моделирования (создаётся модель исследуемого объекта). Результаты решения выводятся в виде зависимостей электрических напряжений в функции времени на экран осциллографа или фиксируются измерительными приборами. Основным назначением АВМ является решение линейных и дифференцированных уравнений.

Достоинства АВМ:

    высокая скорость решения задач, соизмеримая со скоростью прохождения электрического сигнала;

    простота конструкции АВМ;

    лёгкость подготовки задачи к решению;

     наглядность протекания исследуемых процессов, возможность изменения параметров исследуемых процессов во время самого исследования.

Недостатки АВМ:

- малая точность получаемых результатов (до 10%);

- алгоритмическая ограниченность решаемых задач;

- ручной ввод решаемой задачи в машину;

- большой объём задействованного оборудования, растущий с увеличением сложности задачи

Задачи

Контроль и управление. В системах автоматического управления АВМ пользуются, как правило, для определения или формирования закона управления, для вычисления сводных параметров процесса (кпд, мощность, производительность и др.). Если задано математическое выражение, определяющее связь сводного параметра или управляющего воздействия с координатами объекта, АВМ служат для решения соответствующего уравнения. Результат вычислений поступает либо на исполнительный механизм (замкнутая система), либо к оператору. Когда закон управления заранее не определён, а заданы лишь некоторый критерий оптимальности и граничные условия, АВМ применяются в системах поиска оптимального управления и служат математической моделью объекта.

Опережающий анализ, основанный на быстродействии. Многократно решая систему уравнений, описывающих управляемый процесс, учитывая его текущие характеристики, АВМ за короткое время «просматривает» большое число вариантов решений, отличающихся значениями параметров, подлежащих изменению при управлении процессом. Намного опережая ход процесса, АВМ прогнозирует сигналы управления, которые могут обеспечить необходимое качество протекания процесса. В режиме опережающего анализа АВМ выполняют функции либо машин-советчиков, либо управляющих машин, автоматически учитывающих текущие характеристики процесса и управляющих им по оптимальным показателям. Выбор наилучшего режима технологического процесса осуществляется также самонастраивающимися математическими машинами в режиме опережающего анализа.

Экспериментальное исследование поведения системы с аппаратурой управления или регулирования в лабораторных условиях. С помощью АВМ воспроизводится та часть системы, которая по каким-либо причинам не может быть воспроизведена в лабораторных условиях.

Анализ динамики систем управления или регулирования. Заданные уравнения объекта решаются в выбранном масштабе времени с целью нахождения основных параметров, обеспечивающих требуемое протекание процесса.

Решение задач синтеза систем управления и регулирования сводится к подбору по заданным техническим условиям структуры изменяемой части системы, функциональных зависимостей требуемого вида и значений основных параметров. Окончательный результат получается многократным повторением решения и сопоставлением его с принятым критерием близости.

Решение задач по определению возмущений или полезных сигналов, действующих на систему. В этом случае по дифференциальным уравнениям, описывающим динамическую систему, по значениям начальных условий, известному из эксперимента характеру изменения выходной координаты и статистическим характеристикам шумов в измеряемом сигнале определяется значение возмущения или полезного сигнала на входе. АВМ может также служить для построения приборов, автоматически регистрирующих возмущения и вырабатывающих сигнал управления в зависимости от характера и размера возмущений.