Вопрос 9:

Перевод чисел из двоичной системы счисления в системы, родственные двоичной и обратно.

Б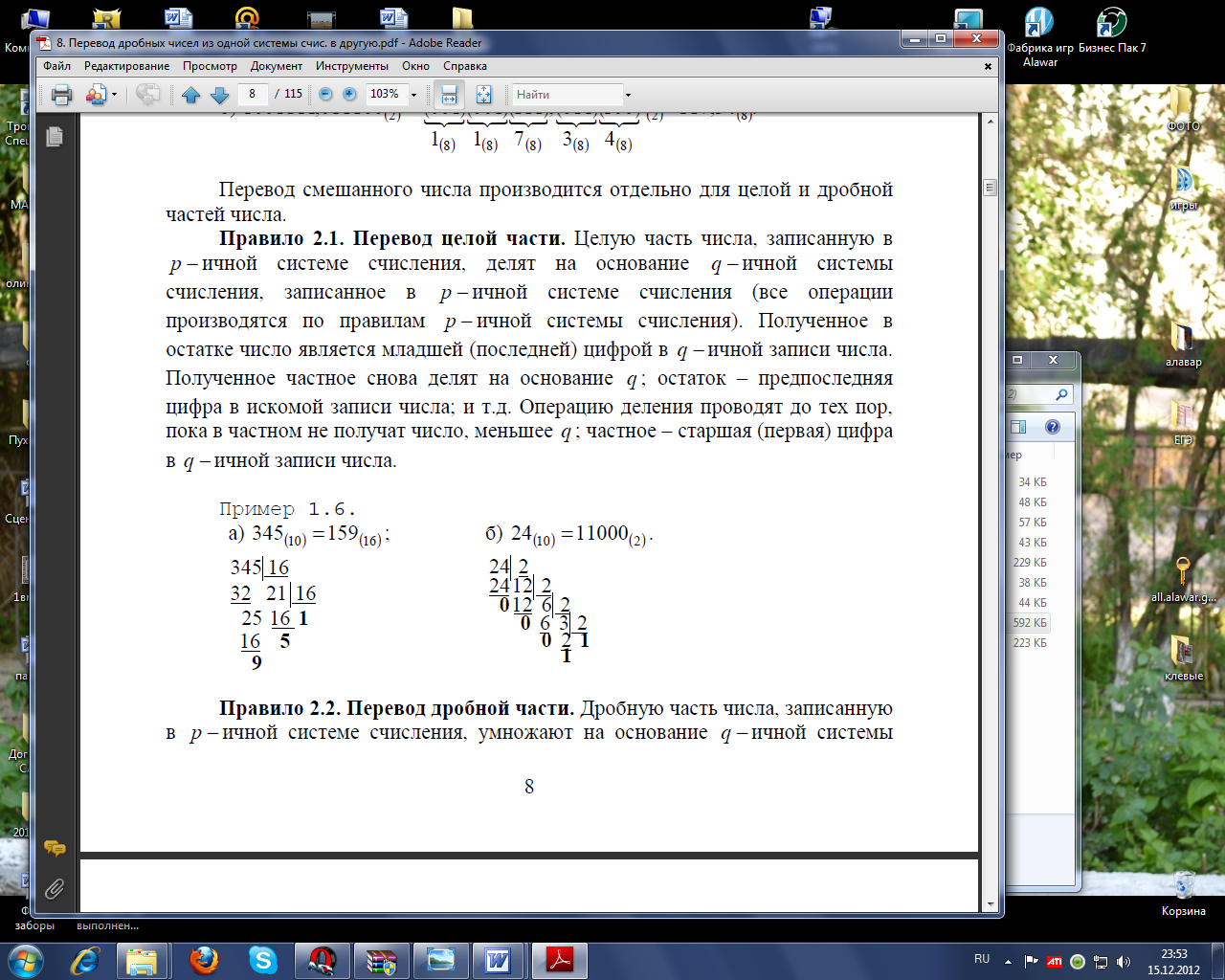 ольшие числа в двоичной системе счисления имеют очень громоздкие записи. Конечно, можно перевести число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоёмки. На помощь приходят системы, родственные двоичной - восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме. Системами счисления родственными двоичной считаются такие системы, основания которых являются значением степени числа 2.

Например, четверичная, восьмеричная и шестнадцатеричная системы счисления являются системами, родственными двоичной.

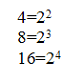
Для перевода чисел из двоичной системы счисления в системы, родственные двоичной, необходимо выполнить следующие действия:

1.Разбить число на некоторое количество разрядов, равное степени числа 2 основания системы, в которую переводим.

2.Если в старших и младших разрядах после разбиения не хватает знаков, то добавить их нулями.

3.По таблице определить значение пары, триады, тетрады и т.п. разрядов, записанных в двоичной системе счисления, соответственно значению в той системе, в которую переводим.

Например, дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в восьмеричную систему счисления разобьём число на триады (т.к. основание числа 2 равно 3), начиная от запятой, вправо и влево: 1.111.010.111.010,011.1 . Разбиение показано точками. В старшей и младшей триадах не хватает разрядов. Дополним их нулями: 001.111.010.111.010,011.100. По таблице определим восьмеричные цифры, соответствующие триадам. Получается восьмеричное число 17272,34.

Рассмотрим ещё один пример: дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в шестнадцатеричную систему счисления разобьём число на тетрады (т.к. основание числа 2 равно 4): 1.1110.1011.1010,0111. В старшей тетраде не хватает разрядов. Дополним их нулями: 0001.1110.1011.1010,0111. По таблице определим шестнадцатеричные знаки, соответствующие тетрадам. Получается шестнадцатеричное число 1EBA,7.

Пусть дано то же число. Для перевода его в четверичную систему счисления разобьём число на пары (т.к. основание числа 2 равно 2): 1.11.10.10.11.10.10,01.11. В старшей паре не хватает одного разряда. Дополним его нулём: 01.11.10.10.11.10.10,01.11. Определим четверичные цифры, соответствующие парам. Получается четверичное число 1322322,13.

Как осуществить обратный перевод:

Пусть дано число 73,62 , записанное в восьмеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру числа запишем в виде триады из 0 и 1, соответствующей значению восьмеричной цифры в двоичной системе счисления: 111.011,110.010.

Рассмотрим ещё один пример: дано число 7В3,Е6, записанное в шестнадцатеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру шестнадцатеричного числа запишем в виде тетрады из 0 и 1,соответствующей значению знака в двоичной системе счисления: 0111.1011.0011,1110.0110.

Перевод чисел из р-ичной позиционной системы счисления в десятичную.

Все позиционные системы счисления, о которых мы говорили выше, строятся по одному общему принципу. Выбирается некоторое число р - основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, т.е. произвольное число в системе счисления с основанием р имеет вид: Если необходимо перевести двоичное число 1011011,11 в десятичную систему, воспользуемся этой формулой. Основание системы р=2, к - коэффициент, указывающий количество знаков в числе влево от запятой, к=7; а - знаки числа с соответствующими им коэффициентами.

Воспользуемся формулой для перевода шестнадцатеричного числа ВF,1D в десятичную систему. Основание системы р=16, к=2.

Пусть необходимо перевести восьмеричное число 254,262 в десятичную систему. Основание системы р=8, к=3