Вопрос 4. Определение количества информации, представленной с помощью знаковых систем. Мера Хартли

Количество информации. Формулы Хартли и Шеннона В 1928 г. американский инженер Р. Хартли предложил научный подход к оценке сообщений. Предложенная им формула имела следующий вид:

I = log2 K ,

Где К - количество равновероятных событий; I - количество бит в сообщении, такое, что любое из К событий произошло. Тогда K=2I.

Иногда формулу Хартли записывают так:

I = log2 K = log2 (1 / р) = - log2 р,

т. к. каждое из К событий имеет равновероятный исход р = 1 / К, то К = 1 / р.

Аддитивная мера определения количества информации

Эта мера предложена в 1928 году американским ученым Хартли, поэтому имеет второе название – мера Хартли. Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита: I = l log h,

Данная формула даёт аналитическое определение бита (BIT - BInary digiT) по Хартли: это количество информации, которое содержится в двоичной цифре.

Единицей измерения информации в аддитивной мере является бит.

Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении.

Вопрос 5. Определение количества информации. Мера шенона

Определение по Шеннону

Клод Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;

в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;

должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Поэтому функция энтропии   должна удовлетворять условиям:

 определена и непрерывна для всех  , где   для всех   и  . (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)

1. Для целых положительных 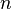 , должно выполняться следующее неравенство:

2. Для целых положительных 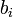 , где 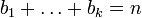 , должно выполняться равенство:

Шеннон показал,^{[источник не указан 633 дня]} что единственная функция, удовлетворяющая этим требованиям, имеет вид:

где   — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии ( ), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислитьматематическое ожидание «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д. (см. цепи Маркова).Определение энтропии Шеннона связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвеллатакже противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.

ВОПРОС 6. Системы счисления. Позиционные и непозиционные системы счисления. Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления.

Различают два вида систем счисления: позиционные и непозиционные системы

Позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;

Непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.Позиционная система счисленияПозиционная система счисления это система счисления в которой значение цифры зависит от разряда.

Разрядом числа называется место цифры в числе.

Наибольший вес имеет самый левый разряд, наименьший вес имеет самый правый разряд.

Нумерация разрядов увеличивается справа налево.

В позиционной системе одна и та же цифра в числе имеет различный вес.

Например: в числе 545 цифра 5 имеет различный вес: первая цифра 5 - показывает количество сотен, вторая цифра 5 - показывает количество единиц.

5 4 5

число сотен число десятков число единиц

У чисел в позиционной системе счисления имеется основание системы - n.

Основанием системы счисления n называют количество цифр в числе используемых для записи чисел.

n принадлежит числовому промежутку от 0 до n-1 включительно.

Непозиционная система счисления Непозиционная система счисления - это системсчисления, в которой значение цифры не изменяется в зависимости орасположения.Примером непозиционной системы счисления служит римская систвкоторой вместо цифр используются латинские буквы.Например: Число 242 можно записать ССXLII (т.е. 100+100+(50-10) .ВОПРОС 7. Перевод простых чисел из одной системы счисления в другую. (на примерах)Наиболее часто встречающиесяM системы счисления – это двоичная, шестнадцатеричная и десятичная. Как же связанымежду собой представления числа в различных системах счисления? Естьразличные способы перевода чисел из одной системы счисления в другую на конкретных примерах.Существует несколько способов перевода чисел из одной системы счисления в другую. Например,1. Перевод подбором коэффициентов ("вручную")2.Перевод целых чисел делением на основание3. Перевод дробных чисел умножением на основание

4. Использование промежуточной системы счисления

Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 29 = 512, а 210 = 1024, что больше начального числа. Таким образом получается число разрядов результата, оно равно 9 + 1 = 10, поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Вторая цифра результата находится так – двойка возводится в степень 9 и вычитается из исходного числа: 567 – 29 = 55. Остаток сравнивается с числом 28 = 256. Так как 55 меньше 256, то девятый разряд – нуль, т.е. результат имеет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27 = 128 > 55, то и он будет нулевым.

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25 = 32 < 55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55 – 32 = 23 справедливо неравенство 24 = 16 < 23, что означает равенство единице пятого разряда. Аналогично получается в результате число 1000110111. Это число разлагается по степеням двойки:

567 = 1·29 + 0·28 + 0·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 1·20

При другом способе перевода чисел используется операция деления в столбик. Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное – 141, остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е. 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.

Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.

Э ти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 162 = 256 < 567 < 163 = 4096. Определяется цифра старшего разряда. 2·162 = 512 < 567 < 3·162 = 768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48 < 55 < 4·16 = 64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55 – 48). Искомое шестнадцатеричное число равно 237.

Второй способ состоит в последовательном делении в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.

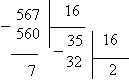
Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.

Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +... + an–1·p1 + an·p0, где a0 ... an – это цифры данного числа в системе счисления с основанием p.

Например, так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·163 + A·162 + 3·16 + F. При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15= 19007. Проще всего переводить числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.

Известный французский астроном, математик и физик Пьер Симон Лаплас (1749–1827) писал об историческом развитии систем счисления, что «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой.» Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.

Перевод чисел из одной системы счисления в другую.

Таблица 1.7. Запис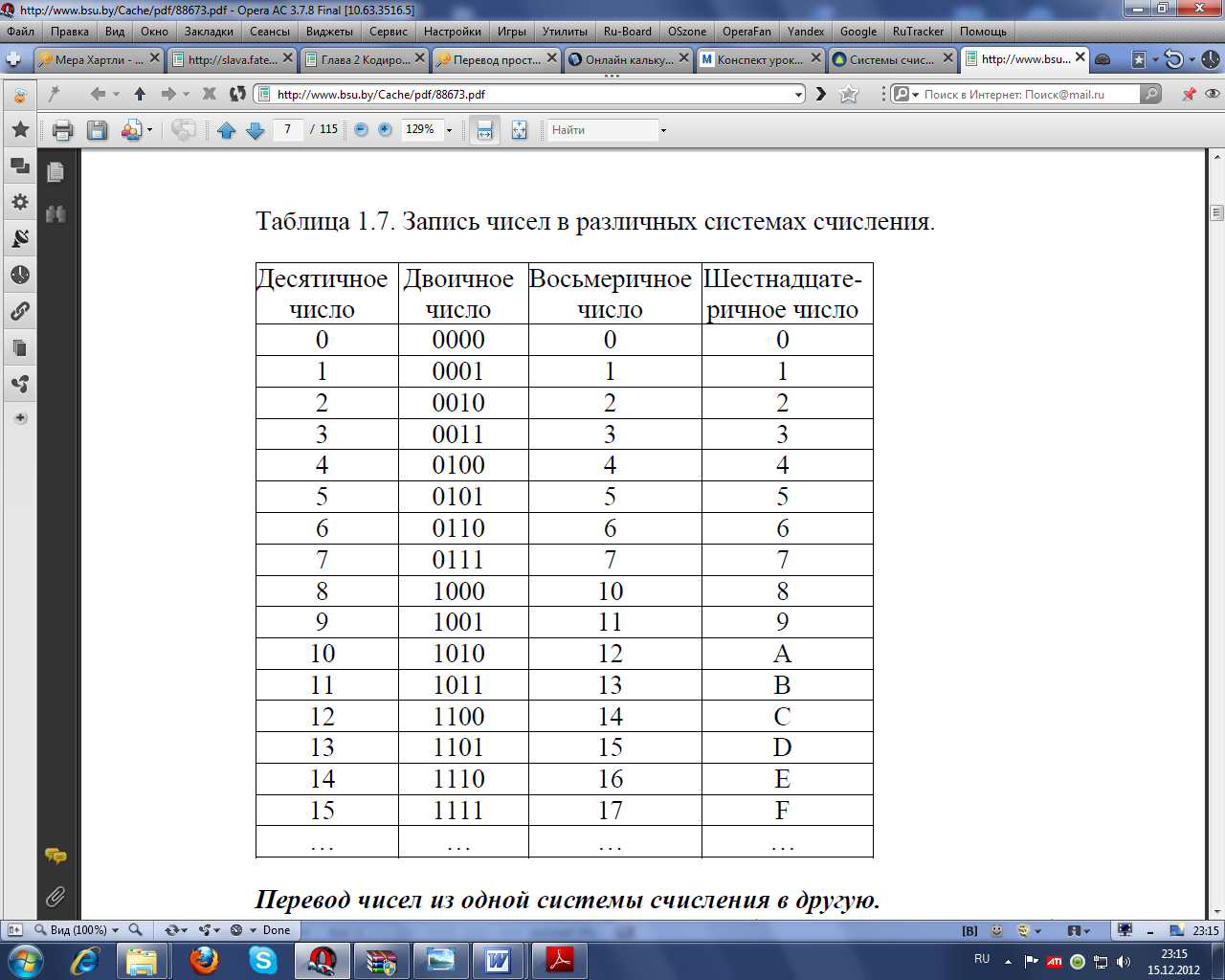 ь чисел в различных системах

Правило 1. Перевод смешанного числа (числа с дробной частью) из

p -ичной системы счисления в q -ичную систему счисления, когда имеет

место соотношение p qk ( k -целое положительное число), осуществляется

поразрядно. Каждая p-ичная цифра заменяется равным ей k -разрядным

числом, записанным в q -ичной системе счисления.

Для упрощения перевода по описанному выше правилу удобно

использовать Таблицу 1.7.

Перевод смешанного числа производится отдельно для целой и дробной

частей числа.

Правило 2.1. Перевод целой части. Целую часть числа, записанную в

p -ичной системе счисления, делят на основание q -ичной системы

счисления, записанное в p -ичной системе счисления (все операции

производятся по правилам p -ичной системы счисления). Полученное в

остатке число является младшей (последней) цифрой в q -ичной записи числа.

Полученное частное снова делят на основание q ; остаток – предпоследняя

цифра в искомой записи числа; и т.д. Операцию деления проводят до тех пор, пока в частном не получат число, меньшее q ; частное – старшая (первая) цифра в q -ичной записи числа.

Правило 2.2. Перевод дробной части. Дробную часть числа, записанную

в p -ичной системе счисления, умножают на основание q-ичной системы

счисления, записанное в p -ичной системе счисления. Целая часть

произведения будет старшей цифрой изображения дроби (первой после

запятой) в q -ичной записи числа. Дробную часть произведения снова

умножают на основание q ; целая часть – следующая цифра после запятой в

q -ичной записи дроби. Процесс продолжают до тех пор, пока дробная часть

не станет нулем или будет получено требуемое количество знаков после

запятой в дробной записи числа. Целые части записывают в q -ичной системе счисления.