11. Математическая постановка непрерывной задачи управления.

Цель задачи оптимального управления объектом – это нахождение экстремума (минимума или максимума) критерия качества 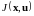. Постановка задачи:

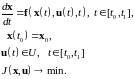(5)

(5) - задача с закрепленным правым концом траектории.

(6)

Примеры задания функционалов :

1. интегральный:

2. терминальный -

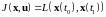
3. смешанный (или функционал Больца)

где и заданные функции.

12. Дискретные задачи оптимального управления.

До сих пор рассматривались непрерывные процессы, которые моделируются системой дифференциальных уравнений. В таких процессах время изменяется непрерывно в пределах какого-то промежутка. Если же время может принимать лишь дискретное множество значений, например , то мы, будем иметь дело с дискретным объектом управления.

Часто дискретные процессы называют многошаговыми. В каждый момент

времени (или на каждом шаге) такие процессы характеризуются двумя наборами переменных: и . Это соответственно вектор состояния и вектор управления. Состояние на 1 + t -м шаге определяется конечно-разностным уравнением

, (7)

где – заданная вектор-функция, дискретная траектория это последовательность

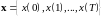
Последовательность 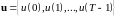называется дискретным управлением. Дискретное управление называется допустимым, если оно удовлетворяет условию

Если при этом условии является решением системы (7), то 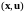является допустимой парой. На множестве допустимых пар задается функционал , и задача выглядит следующим образом:

Пример задания функционалов :

1. интегральный ;

2. терминальный ;

3. смешанный

13. Однопродуктовая динамическая макроэкономическая модель.

Прежде чем переходить к построению абстрактных моделей управляемых процессов и, в частности, к моделям развития экономики, рассмотрим механизм построения нескольких простых примеров экономической динамики.

Исследование взаимосвязей элементов производства вне общественной формы реализации продукции (рис.1) приводит к производственно-технологической интерпретации экономики.

Внешняя среда

Рис. .1. Принципиальная схема производства и распределения продукции

Природные

ресурсы W^s

W

K

Труд L

потребление C

Ввод в действие

капитала

Капитал

K

Чистые

инвестиции

Непроизводственное

Валовые инвестиции I

P_I

P_y

Конечный

продукт

Y

продукт

X

P_x

Валовой

Производство

Ввод в действие

Y

Амортизационные отчисления A

Экономика

На рис..2 выделены факторы, характеризующие производство: живой труд (L), средства труда (основные производственные фонды, капитал K) и предметы труда, (W^s) – ресурсы.

Результатом производственной деятельности является валовой продукт (X), распределяемый в блоке P_Х на производственное потребление (W) и конечный продукт (Y). В свою очередь, конечный продукт (Y) делится в блоке распределения P_Y на капитальные валовые вложения (I) и на непроизводственное потребление (C).

Капитальные валовые вложения I, входящие в блок P _I , делятся на амортизационные отчисления (A) и чистые инвестиции, идущие на расширение производственных фондов.

Ограничимся изучением взаимосвязей между синтетическими показателями верхнего уровня экономической иерархии. Одним из подходов к решению данной проблемы является построение однопродуктовой макроэкономической модели. С помощью этой модели изучают свойства и тенденции изменения взаимосвязанных агрегированных (объединенных в одну систему) показателей, таких, как валовой и конечный продукты, трудовые ресурсы, производственные фонды (капитал), инвестиции, потребление и т.д. Так, на макроуровне блок распределения P _X показывает взаимосвязь между валовым продуктом X, производственным потреблением W и конечным продуктом Y:

X=W + Y. (1)

Блок P_Y делит конечный продукт на две составляющие: валовые капитальные вложения I и непроизводственное потребление C, т.е.

Y= I + C. (2)

Инвестиции составляют материальную основу наращивания и перевооружения производства. За их счет осуществляется ввод в действие основных производственных фондов. Однако этот процесс сопряжен с определенными трудностями, одной из которых является учет распределенного запаздывания прироста основных фондов от реализации капитальных вложений. В экономико-математическом моделировании имеется ряд подходов к описанию этой взаимосвязи.

В однопродуктовой модели делается предположение, что валовые инвестиции полностью расходуются на прирост основных производственных фондов, в том же году и на амортизационные отчисления:

а) в дискретном варианте эта взаимосвязь имеет вид

I = q ∆K_t + A; (3)

∆K_t = К _t+1 - K_t ;

A = µ K_t

где ∆K_t – прирост основных производственных фондов в году t;

q – параметр модели;

А – амортизационные отчисления;

µ – коэффициент амортизации;

K_t – основные производственные фонды в году t;

б) аналогом уравнения (3) в непрерывном варианте является

Отсюда можно получить дифференциальное уравнение динамики фондов

(4)

Объединяя уравнения связи (1) – (4), получим однопродуктовую динамическую макромодель в дискретном варианте:

X _t = W_t + q ∆K_t + µ K_t + C_t .

Если считать производственные затраты W пропорциональными выпуску продукции X, т.е.

W = aX, (5)

то в дискретном варианте однопродуктовая динамическая модель примет вид

X _t = aX _t + q ∆K_t + µ K _t + C _t, (6)

откуда можно получить ∆K_t =- µ K _t + [(1 - a) X _t - C _t ],

а в непрерывном варианте

(6.1)

Модель (6) называется моделью оптимального распределения капитальных вложений в отрасли. Экономический процесс можно рассматривать как управляемый, если считать управлением , - состоянием. На переменные состояния и управления следует наложить естественные ограничения:

(6.2)

где – заданное начальное значение основных фондов, – известные постоянные, или зависящие от времени функции. Для оценки протекающего процесса введем в рассмотрение критерий качества:

(6.3)

Теперь можно сформулировать задачу оптимального управления: требуется найти пару, которая удовлетворяет уравнению (6.1), условиям (6.2) и доставляет минимум критерию качества (6.3). Так как функционал (6.3) состоит из двух слагаемых, то его минимизация означает, во-первых, экономию капиталовложений, а во-вторых, максимизацию основных фондов в конце рассматриваемого отрезка времени (так как второе слагаемое входит со знаком минус). Числа β α, – это весовые коэффициенты,

α>0, β>0. Если α>β, то приоритет отдается первому требованию, если α<β – то второму.

В некоторых случаях используют упрощенные варианты однопродуктовой динамической модели.