10. Экономическая система как объект управления.

Любое управление предполагает наличие объекта управления (управляемой системы), субъекта управления (управляющей системы) и внешней среды.

Основное назначение управляющей системы – поддерживать установленный и по каким-либо свойствам признанный нормальным режим работы объекта управления, а также обеспечивать нормальное функционирование отдельных элементов объекта управления в условиях воздействия внешней среды. Объект управления во взаимодействии с управляющей системой – субъектом управления образует замкнутую систему управления.

X y

Рис. .1. Схема замкнутой системы управления (упрощенный вариант).

Х – вектор воздействия внешней среды на объект управления;

Y – вектор реакции на воздействие X.

Связь, с помощью которой управляющая система – субъект управления – воздействует на объект управления, если эта связь имеется, называется обратной связью. Входным сигналом для обратной связи служит выходной сигнал системы Y. (Система управления без обратной связи – светофор). Если этот сигнал не соответствует целям управления замкнутой системой, то управляющая система вырабатывает воздействие обратной связи Δ X, которое вместе с сигналом X поступает на вход объекта управления (X, Y, Δ X – векторы соответствующих размерностей).

В правильно работающей с точки зрения поставленной цели системе сигнал X + ΔX должен способствовать улучшению качества функционирования замкнутой системы управления. Количественные оценки степени достижения цели в модели управления даются в виде значений функционала (целевой функции), а условия, в рамках которых функционирует система, – в виде ограничений модели. Цель оптимального управления – нахождение наилучшего относительно принятой целевой функции критерия оптимизации. При отсутствии обратной связи (упомянутый выше светофор) движение регулируется по заранее заданной программе независимо от фактических потоков автомобилей, т.е. состояния системы на выходе. Другие примеры управления без обратной связи: уставы, кодексы инструкции и наставления. Изложенное выше относится к характеристике систем управления практически любой природы – экономической, физической, производственно-технологической. В процессе функционирования предприятия одновременно ставятся цели добиться максимально возможных прибыли и выпуска продукции в натуральном или стоимостном выражении, выдержать необходимые потребителю ее номенклатуру или ассортимент, уровень качества, снизить удельную себестоимость и т.д.

Некоторые из этих показателей могут быть противоречивыми. Например, первый и последний. Стремление к максимальному валовому выпуску продукции (в стоимостном или натуральном выражении) одновременно ведет и к валовому росту себестоимости. Иначе быть не может, так как производство каждого дополнительного изделия сопряжено с дополнительными затратами, т.е. чем больше выпускается продукции, тем больше становится и суммарная себестоимость производства. Ограничение такой себестоимости – противоположное требование к росту выпуска продукции. Пользуясь современной терминологией, можно утверждать, что задачи управления экономикой плохо структурированы и не всегда модель может быть построена однозначным образом. Прежде всего, цели функционирования многих экономических и особенно социально-экономических систем не всегда возможно четко сформулировать.

Дифференциальные уравнения служат основой при конструировании моделей не только в экономике, но и в других областях науки и техники. Очень часто в качестве модели выбирается система обыкновенных дифференциальных уравнений:

, (1)

где – некоторые заданные функции. Независимую переменную t в системе (1), описывающей некоторый управляемый процесс, принято называть временем. Переменные характеризуют состояние объекта управления в момент времени t и называются выходными переменными. Вектор-столбец 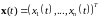называется вектором состояния или вектором выхода. При каждом t состояние – это элемент n-мерного векторного пространства , которое называют пространством состояний, или фазовым пространством. В связи с этим переменные состояния называют иногда фазовыми переменными. Размерность фазового пространства – число выходов. Пусть U – некоторое множество в пространстве E^m . Под допустимым будем понимать управление, которое при каждом удовлетворяет условию и каждая компонента которого кусочно-непрерывна, т.е. непрерывна для всех рассматриваемых t за исключением конечного числа точек, в которых она может иметь разрыв первого рода. (Разрыв первого рода по определению предполагает существование конечных пределов слева и справа в точке разрыва). Предположим теперь, что нам известно состояние исследуемой системы в начальный момент времени. При каждом фиксированном допустимом управлении мы будем иметь задачу Коши:

(2)

Относительно функции , всюду будем предполагать, что она определена при всех непрерывна по аргументам , непрерывно дифференцируема по x и кусочно-непрерывна по t . При сделанных предположениях для каждого допустимого управления и начального условия существует единственное непрерывное решение задачи Коши (2), определенное, по крайней мере, в некоторой окрестности начальной точки. В дальнейшем будем рассматривать только такие процессы управления, для которых решение задачи Коши (2) существует на всем отрезке и непрерывно на нем. Это решение будем называть траекторией, выходящей из точки . Соответственно, значение называют левым концом траектории, – правым концом траектории системы (2).

Рассмотрим множество M произвольной природы. Говорят, что на множестве M задан функционал F, если известно правило, по которому каждому элементу ставится в соответствие определенное действительное число. При этом пишут: F(v) =c. Множество M называется областью задания, или областью определения функционала. Элементы множества M называют аргументами функционала. Функционал осуществляет отображение множества M на множество действительных чисел и является обобщением понятия функции. Приведем примеры функционалов.

Пример 1. Пусть M – это множество плоских фигур, ограниченных замкнутыми кривыми. Каждой фигуре v поставим в соответствие ее площадь . Тем самым будет определен функционал F с областью задания M.

Пример 2. Пусть M – это множество функций, заданных и непрерывных на отрезке [a, b]. Каждой функции y (x) из M поставим в соответствие действительное число F (y), равное интегралу от этой функции на отрезке [a, b];

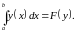
Будем рассматривать в качестве области задания функционалов пространство непрерывных функций, определенных на отрезке [a,b], которое обозначается C [a,b].

Определение 1. Расстоянием между двумя функциями y(t), x(t) называется число .

Определение 2. ε -окрестностью функции x(t) называется совокупность функций y(t), расстояние которых от x(t) меньше ε: .

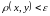Определение 3. Говорят, что функционал достигает в точке

относительного (или локального) минимума (максимума), если для всех функций , принадлежащих некоторой ε – окрестности функции , имеет место неравенство

(3)

Если неравенство (3) выполняется для всех функций из множества C[a,b], то говорят, что функционал F (x) достигает на C [a, b] абсолютного (или глобального) минимума (максимума) в точке x* (t).

Каждая точка, в которой достигается экстремум, называется решением задачи (3) (локальным или глобальным). Решение может быть не одно.

Пусть U – некоторое подмножество C[a,b]. Рассмотрим задачу отыскания экстремума на множестве U:

(.4)

Задачу (4) называют задачей на условный экстремум, в то время как задача (3) – это задача на безусловный экстремум (или задача безусловной оптимизации). Множество U может быть задано всевозможными способами, в том числе с помощью равенств или неравенств, например

Задача минимизации функционала

эквивалентна задаче максимизации

.

в том смысле, что множества глобальных, локальных, строгих или нестрогих решений этих задач соответственно совпадают.