
- •1. Основные типы математических моделей в экономике. Этапы их разработки.
- •2. Оптимизационные задачи. Необходимые и достаточные условия оптимальности.
- •3. Задача условной оптимизации.
- •4. Линейное программирование. Задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии.
- •5. Теоремы о выпуклых множествах.
- •6. Теоремы о допустимых решениях канонической задачи.
- •7. Геометрический метод решения задач линейного программирования.
- •8. Симплексный метод.
- •9. Двойственные задачи линейного программирования.
- •10. Экономическая система как объект управления.
- •11. Математическая постановка непрерывной задачи управления.
- •12. Дискретные задачи оптимального управления.
- •13. Однопродуктовая динамическая макроэкономическая модель.
- •14. Частные случаи: открытая однопродуктовая динамическая модель Леонтьева; замкнутая однопродуктовая модель Леонтеьва.
- •15. Модель оптимального распределения капитальных вложений между отраслями.
- •16. Принцип максимума Понтрягина.
- •17. Задача оптимального управления для линейной системы с квадратичным функционалом без ораничений на управление.
- •18. Принцип максимума для дискретных задач.
8. Симплексный метод.
Если условия задачи линейного программирования непротиворечивы, то область ее допустимых решений образует выпуклый многогранник в n-мерном пространстве. При этом оптимальное решение, если оно существует, обязательно достигается в некоторой вершине многогранника (возможно, и более чем в одной). Таким образом, чтобы найти решение задачи линейного программирования, достаточно перебрать лишь планы, соответствующие вершинам многогранника допустимых решений. Симплексный метод состоит в том, что производится проверка, достигнут ли в данной вершине максимум целевой функции, если план не оптимальный, то производится переход к такой соседней вершине многогранника, которая обеспечивает большее (или, в крайнем случае, равное предыдущему) значение целевой функции. Повторное применение указанной процедуры приводит, в конце концов, к вершине, соответствующей оптимальному плану. Количество шагов (переходов) от исходной вершины до точки оптимума обычно представляет собой величину одного порядка с числом уравнений (ограничений) решаемой задачи. Для использования симплексного метода задача должна быть приведена к каноническому виду. Для реализации метода необходимо освоить три основных элемента:
способ определения какого-либо допустимого первоначального базисного решения;
правила перехода к лучшему (нехудшему) решению;
критерий проверки оптимальности найденного решения.
Алгоритм симплексного метода рассмотрим на примере:
 (1)
(1)
Переходим к системе
 (2)
(2)
Для
нахождения допустимого первоначального
базисного решения разобьём все переменные
на основные и неосновные переменные.
Определитель при переменных
 отличен от нуля. Эти переменные берем
в качестве основных переменных на первом
этапе задачи. Если выбранные переменные
имеют те же знаки, что и соответствующие
им свободные члены то решение будет
допустимым (все переменные положительны).
отличен от нуля. Эти переменные берем
в качестве основных переменных на первом
этапе задачи. Если выбранные переменные
имеют те же знаки, что и соответствующие
им свободные члены то решение будет
допустимым (все переменные положительны).
I
шаг
– основные переменные
,
неосновные--
![]() .
.
Выразим основные переменные через неосновные
 (3)
(3)
Положим
неосновные переменные
![]() .
Получим вектор
.
Получим вектор
![]() ,
который является допустимым решением.
Проверим его оптимальность
,
который является допустимым решением.
Проверим его оптимальность
 .
Ясно, что если увеличить неосновные
переменные, то целевая функция возрастет.
Можно перейти к другому базису, в котором
либо
.
Ясно, что если увеличить неосновные
переменные, то целевая функция возрастет.
Можно перейти к другому базису, в котором
либо
![]() ,
либо
,
либо
 будет основной переменной, а значит
больше нуля. Выберем
т.к. коэффициент при этой переменной
целевой функции больше. Система (3)
накладывает ограничение на рост
,
поскольку все переменные должны быть
неотрицательными (
будет основной переменной, а значит
больше нуля. Выберем
т.к. коэффициент при этой переменной
целевой функции больше. Система (3)
накладывает ограничение на рост
,
поскольку все переменные должны быть
неотрицательными ( -
неосновная переменная), получим
-
неосновная переменная), получим

Таким
образом, возможное наибольшее значение
переменной
равно 5. При этом значении
переменная
 .
.
II – шаг
Основные
переменные
 ,
неосновные
,
неосновные
 .
Выразим, новые основные переменные
через неосновные
.
Выразим, новые основные переменные
через неосновные
 (4)
(4)
Второе
базисное решение
 является допустимым. Проверим его
оптимальность. Целевая функция
является допустимым. Проверим его
оптимальность. Целевая функция
 .
.
 .
.
Найдем
ограничения на
 .
.
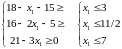 (5)
(5)

Тогда
переменная
 переходит в неосновные.
переходит в неосновные.
III
шаг Основные
переменные
 ,
не основные
,
не основные
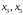 .
Выразим, новые основные переменные
через не основные
.
Выразим, новые основные переменные
через не основные
 (6)
(6)
Получим
вектор допустимых решений
 .
.
Проверим
его оптимальность. Целевая функция
 . (7)
. (7)
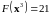
Третье
решение тоже не является оптимальным
т.к. положительный знак при
 .
Найдем ограничения на
.
.
Найдем ограничения на
.
 (8)
(8)
Положим
 .
Тогда
.
Тогда
 переходит в неосновные.
переходит в неосновные.
IV
шаг Основные
переменные
 ,
не основные
,
не основные
 .
Выразим, новые основные переменные
через не основные переменные
.
Выразим, новые основные переменные
через не основные переменные
 (9)
(9)
Решение
 .
Проверим его оптимальность. Целевая
функция
.
Проверим его оптимальность. Целевая
функция
 .
(10)
.
(10)
 .
.
Поскольку в (10) положительных коэффициентов при неосновных переменных нет, то мы нашли оптимальное решение.
Сформулируем критерий оптимальности. Если при отыскании максимума линейной функции в выражении этой функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.
