25.Аппроксимация функции с помощью кубического сплайна

Сплайны – многочлены 3-ей степени, построенные специальным образом.

Для пары соседних узлов многочлен имеет вид:

Для определения коэффициентов а, b, c, d на всех (N-1) отрезках необходимо получить 4*(N-1) уравнений.

Часть уравнений составляется из условия прохождения функцией j(х) через заданные точки эксперимента

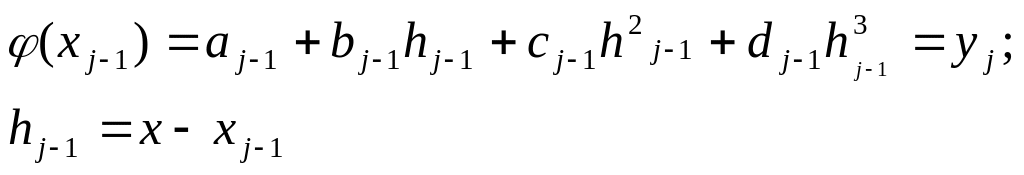
, j=2,3…N

Так получаем 2*(N-1) уравнений.

Для получения недостающих уравнений используем условие непрерывности 1-ых и 2-ых производных в узлах интерполяции. Приравнивая в каждом внутреннем узле значение этих производных, вычисленных в правом и левом от узла интерполяции интервалах, получим еще 2*(N-1)-2 уравнения:

Ещё 2 уравнения получим из условия закрепления концов сплайна. При свободном закреплении концов можно приравнять к нулю кривизну линий в этих точках (эта функция – свободный кубический сплайн) 2-ые производные в этих точках равны нулю.

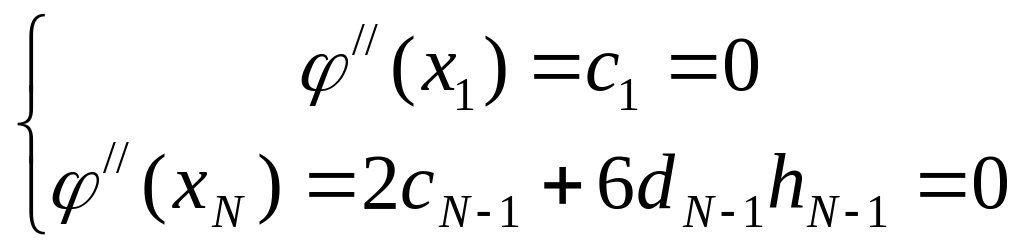
С целью экономии машинного времени:

Сначала находят а_j-1= y_j-1, затем

Далее подстановкой и

В окончательном виде получим с₁=0, с_N-1=0,

По найденным с_j находят b и d.

На каждом интервале своя сплайн функция.

При интерполяции сплайнами следует чаще выбирать узлы интерполяции на нелинейных участках изменения функции.

26 Полиномы Чебышева(пч)

ПЧ – полином наименее отклоняющийся от 0 на отрезке [-1;1].

Мн-ном Чебышева наз-ся ф-ция: T_n(x) = cos(n*arcos(x)), n из N, x из [-1;1].

n=0, T₀=1 n=1, T₁(x)=x.

α = arcos(x) -> T_n-1 = cos((n-1)* α), T(_n+1) = cos((n+1)* α)

cos((n+1)*α) = cos(n*α)*cos(α) – sin(n*α)*sin(α)

cos((n-1)*α) = cos(n*α)*cos(α) + sin(n*α)*sin(α)

cos((n+1)*α)+ cos((n-1)*α) = 2* cos(n*α)*cos(α)

T_n+1(x)+T_n-1(x) = 2xT_n(x) => (2) T_n+1(x) = 2xT_n(x)-T_n-1(x)

T₂(x) = 2x²-1

T₃(x) = 2x(2x²-1)-x = 4x³-3x

Анализ формулы (2) позволяет утверждать след:

1.все ф-ции многочлены степени эн

2.все степени возростают с ростом эн, старший коэфф имеет вид 2^n-1xⁿ

3.при четн эн все степени четные

Св-ва:

1.многочлен имеет на [-1;1] ровно эн различн действ корней

2.корни ПЧ перемежаются с точками их наиб и наим знач = -1 и 1

3.из всех мн-нов степ эн нормир ПЧ отклоняется от 0 наим на [-1;1]

если в качестве узлов интерполирования братькорни ПЧ то остаточный член будет иметь вид: R_n(f,x)<=((b-a)ⁿ⁺¹/2²ⁿ⁺¹)M_n+1

29. Метод Рунге-Кутта.

Для повышения точности вычисления значений функции требуется проведение дополнительных вычислений внутри интервала h, то есть между xi и xi+1. Метод Рунге-Кутта даёт набор формул для расчёта координат внутренних точек, требуемых для достижения точности, то есть ошибки на каждом шаге, порядка h4. Расчёты при использовании этого метода производятся по формуле

yi+1=yi+(k0+2k1+2k2+k3)/6

Здесь k0=h*f(xi,yi),

k1=h*f(xi+h/2, yi+k0/2),

k2=h*f(xi+h/2, yi+k1/2),

k3=h*f(xi+h, yi+k2)

Метод Эйлера и его модификация по существу являются методами Рунге-Кутта первого и второго порядка соответственно. По сравнению с ними метод Рунге-Кутта обеспечивает более высокую точность. Это позволяет увеличить шаг интегрирования h. Допустимая погрешность на шаге определяет его максимальную величину.