
- •1.Прямые методы решения слау.
- •2)Lu-разложение.
- •2.Метод трехдиагональной матричной прогонки.
- •4. Задачи линейного программирования(лп). Регуляризация задач лп.
- •5.Регуляризация плохо обусловленных слау.
- •6.Обзор задач линейной алгебры. Уточнение эл-ов приближ. Обратной ма-цы .
- •7. Принцип сжатых отображений в огр.Обл. Банахова пр-ва.
- •8.Методы решения нелинейных одномерных у-ий.
- •9 Не лок метод Ньют (квазиньют процесс)
- •10,Метод секущих
- •11. Методы решения систем нелинейных уравнений. Квазиньютоновские методы.
- •12. Интерполирование. Конечные разности, разностные отношения и их свойства.
- •15,Численное дифференцирование
- •16. Регуляризация задачи численного дифференцирования
- •18. Малая и большая формула трапеций.
- •19. Малая и большая формула средних прямоугольников и ее остаточный член.
- •20.Формула Симпсона
- •21.Квадратурные формулы более высокого порядка точности
- •23. Правило Рунге — Ромберга
- •24. Восстановление функций по мнк.
- •25.Аппроксимация функции с помощью кубического сплайна
- •26 Полиномы Чебышева(пч)
- •29. Метод Рунге-Кутта.
- •33.Жёсткие начальные задачи. Неявный метод Эйлера и его устойчивость.
- •34.Жёские начальные задачи. Неявный метод средней точки и его устойчивость.
- •35.Жёсткие задачи. Неявный метод трапеций и его устойчивость.
- •36. Краевые задачи. Редукция к задачам Коши.
- •37.Краевые задачи. Метод диф.Прогонки.
- •42. Метод наименьших квадратов решения линейных краевых задач.
16. Регуляризация задачи численного дифференцирования
Пусть имеется двухточечн апрокс произв-й n=1, f’(x0)~(f(x0+h)-f(x0))/h, что соотв-ет замене ф-ции f линейной ф-цией, ε-погрешность вычислениязнач-й ф-ции. При выч-ии f”(x0) образ-ся предельная абсол. погр-ть 2ε/h-погр-ть прибл. Выч-ния произв по знач-м ф-ции. С другой стороны в рез-те замены произв-й её разностным аналогом мы имеем погрешность R1'=M2h'/2; g(h)=2E/h+h M2/2->min, g’(h)=-2E/h2+ M2/2=0, h=√4E/ M2=O(√E).Чистое диффер-ние-не корректная зад и требует построения регуляризующего алг.-ма. Простейший регуляризатор для числ-го алг-ма – регуляризация по шагу. Для для двухточ-ой аппроксимации шаг д.б. порядка О(√ε),ε-погрешность вычислениязнач-й ф-ции.
17. Численное интегрирование. Формулы Ньютона-Котесса
Если ф-ция задана таблично, или интеграл неберущийся, то прим. числ. интегр. Простейшие ф-мы: ф-ла трапеций и ср-х прямоуг-в. Ф-ла Ньют-Кот:∫f(x)dx=∑Ai f(xi)+R, Ai-квадратурные коэф, xi-квадр-е узлы. Рассм. ∫f(x)dx=∫(Pn(x)-Rn(f,n))dx=∫Pn(x)dx+Rn. Расм. равном-ю сетку:X1=a, Xn=b, h=(b-a)/n, Xi=Xo+ih, t=(x-xo)/h, dx=h dt, ω(x)=(x-xo)(x-x1)…(x-xn)=th(t-1)h(h-2)h…(t-n)h=hn+1П(t); ω’(t)=ih(i-1)h…h(-h)(-2h)…(-(n-i))h=i!hi(n-i)!hn-i(-1)n-i=hni!(n-i)!(-1)n-I. Ai=(b-a)Bi, Bi=((-1)n-i/ni!(n-i)!)*∫П(t)dt/(t-i)-коэф Ньют-Кот, не зависит от подинт. ф-ции, обл. итегрир, числа точек n.Пусть n=1,f(x0)=f(a), f(x1)=f(b), Bo=1/2, B1=1/2: ∫f(x)dx=(b-a)∑Bi f(xi)+R1=((b-a)/2)*(f(a)-f(b))+R1-ф-ла трапеции
18. Малая и большая формула трапеций.
Заменим ф-цию на отрезке [a;b] многочленом Лагранжа 1-й степени с узлами х0=а, х1=b. (1)F=∫f(x)dx≈((b-a)/2)*(f(a)-f(b)). Для нахождения погр-ти разл f(x) по ф-ле Тейлора: f(x)=f(x*)+(x-x*)f(x’)+0.5(x-x*)2+…, х*=0.5(a+b). Член погрешности R=∫f(x)dx-((b-a)/2)*(f(a)-f(b)) ≈-(b-a)3f’’(x*)/12. Интеграл разбивают на сумму инт-в по шагам сетки и к каждому шагу применяют ф-лу(1), получ обобщ-ю ф-лу трапеций ∫f(x)dx≈∑(Xi-Xi-1)(f i-1 +fi)/2, R≈-∑(Xi-Xi-1)3f’’’(x*i)/12. На равномерной сетке она упрощается: ∫f(x)dx≈ h(fo/2+ f1+f2+…+f N-1+f N), R≈-∑h3f’’’(x*i)/12≈-h2∫f’’’(x)dx/12, h=Xi-Xi-1. Для справедливости этой оценки необх существ-ние непрер-й f’’’(x), если она кус-но-непр-на, то |R|≤(b-a)h2M2/12, M2 =max|f’’’(x)|.
19. Малая и большая формула средних прямоугольников и ее остаточный член.
Рассм.
простейшие ф-лы приближенного
интегрирования
![]() ;
;![]() ф-ла
левых прямоугольников;
ф-ла
левых прямоугольников;![]() ф-ла правых прямоугольников;
ф-ла правых прямоугольников;![]() ф-ла средних прямоугольников.
Пусть
ф-ла средних прямоугольников.
Пусть
![]() ,
,![]()
![]()
![]() (1)
(1)
![]() (2);
(2);
![]() ;
;
![]() ;
;
![]()
![]()
![]() (3)
(3)
Пусть
![]() ,
,
![]()
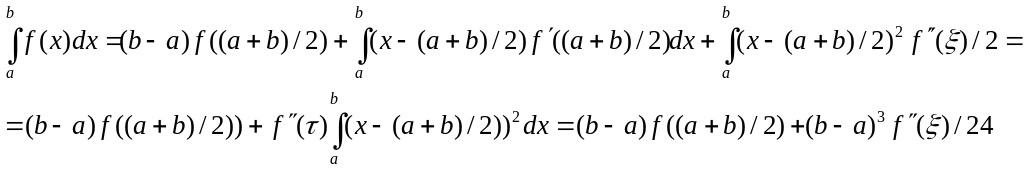
![]() (5); Разобьем
[a;b]
на n
частей и к каждой применим свою ф-лу
пр-ков.
(5); Разобьем
[a;b]
на n
частей и к каждой применим свою ф-лу
пр-ков.
![]() (6)
–большая ф-ла
пр., где
h=(b-a)/2.
При
(6)
–большая ф-ла
пр., где
h=(b-a)/2.
При
![]() ,
(6) - ф-ла л.пр-ков; при
,
(6) - ф-ла л.пр-ков; при
![]() ,
(6) - ф-ла пр.пр-ков; при
,
(6) - ф-ла пр.пр-ков; при
![]() (6)
- ф-ла ср.пр-ков.
(6)
- ф-ла ср.пр-ков.
![]()
![]()
![]()
20.Формула Симпсона
В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки (xj, f(xj)), где j = i-1; i-0.5; i, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:
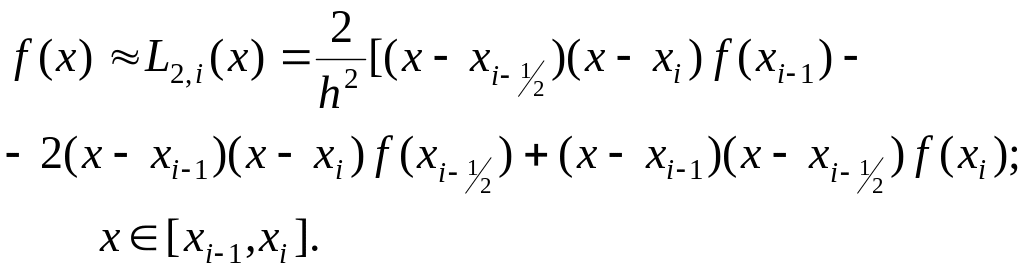 (2.14)
(2.14)
Проведя интегрирование, получим:
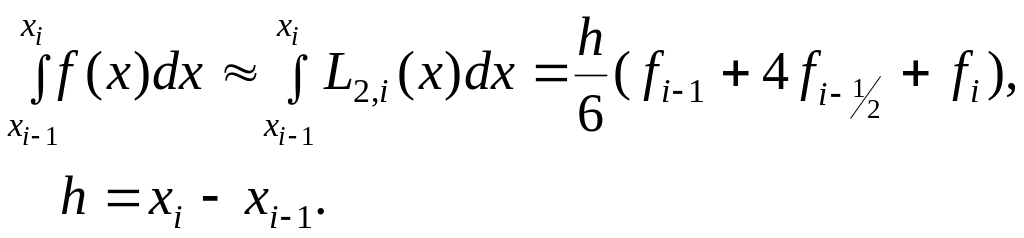
![]() (2.15)
(2.15)
Это и есть формула Симпсона или формула парабол. На отрезке [a, b] формула Симпсона примет вид
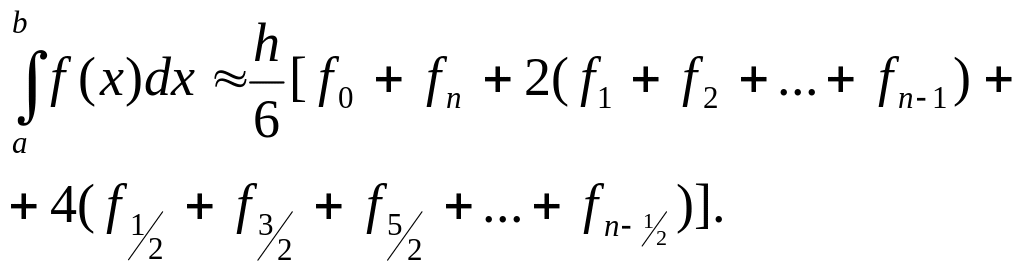 (2.16)
(2.16)
Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:
![]() (2.17)
(2.17)
Тогда формула Симпсона примет вид
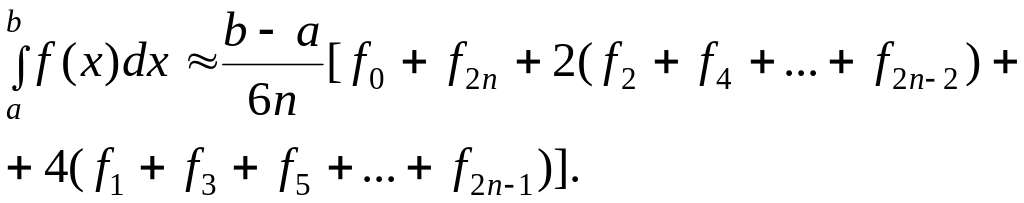 (2.18)
(2.18)
Погрешность формулы (2.18) оценивается следующим выражением:
![]() , (2.19)
, (2.19)
где h·n
= b
- a,
![]()
Таким образом, погрешность формулы Симпсона пропорциональна O(h4).
Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на четное число интервалов.
