
- •1.Прямые методы решения слау.
- •2)Lu-разложение.
- •2.Метод трехдиагональной матричной прогонки.
- •4. Задачи линейного программирования(лп). Регуляризация задач лп.
- •5.Регуляризация плохо обусловленных слау.
- •6.Обзор задач линейной алгебры. Уточнение эл-ов приближ. Обратной ма-цы .
- •7. Принцип сжатых отображений в огр.Обл. Банахова пр-ва.
- •8.Методы решения нелинейных одномерных у-ий.
- •9 Не лок метод Ньют (квазиньют процесс)
- •10,Метод секущих
- •11. Методы решения систем нелинейных уравнений. Квазиньютоновские методы.
- •12. Интерполирование. Конечные разности, разностные отношения и их свойства.
- •15,Численное дифференцирование
- •16. Регуляризация задачи численного дифференцирования
- •18. Малая и большая формула трапеций.
- •19. Малая и большая формула средних прямоугольников и ее остаточный член.
- •20.Формула Симпсона
- •21.Квадратурные формулы более высокого порядка точности
- •23. Правило Рунге — Ромберга
- •24. Восстановление функций по мнк.
- •25.Аппроксимация функции с помощью кубического сплайна
- •26 Полиномы Чебышева(пч)
- •29. Метод Рунге-Кутта.
- •33.Жёсткие начальные задачи. Неявный метод Эйлера и его устойчивость.
- •34.Жёские начальные задачи. Неявный метод средней точки и его устойчивость.
- •35.Жёсткие задачи. Неявный метод трапеций и его устойчивость.
- •36. Краевые задачи. Редукция к задачам Коши.
- •37.Краевые задачи. Метод диф.Прогонки.
- •42. Метод наименьших квадратов решения линейных краевых задач.
1.Прямые методы решения слау.
Все методы решения СЛАУ можно разбить на два класса: прямые и итерационные. Прямые методы - методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (поэтому прямые методы наз. ещё точными методами)
Мы рассматриваем численное решение таких СЛАУ, у которых число уравнений совпадает с числом вещественных неизвестных, причем предполагается наличие единственного решения, если существование и единственность не следует из каких-либо условий.
Итак, изучается вопрос о численном решении системы …(1) или иначе, векторно-матричных уравнений Ах=b. (1a) где b – вектор свободных членов x - вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а А - вещественная n*n-матрица коэффициентов данной системы. Эффективность способов решения системы (1) во многом зависит oт структуры и свойств матрицы А: размера, обусловленности, симметричности, заполненности (т.e. соотношения между числом ненулевых и нулевых элементов), специфики расположения ненулевых элементов в матрице и др.
Прямые методы решения СЛАУ:
1.Метод Гаусса(с выбором главного элемента по столбцам).
2.LU-разложение.
3.Метод квадратного корня.
1) Метод Гаусса. Суть: последовательное исключение неизвестных. Поэтапно приводим систему к треугольному виду, исключая последовательно сначала x1 из второго, третьего, …, n-го у-ний, затем x2 из 3-го, 4-го,..,n-го у-ий преобразованной системы, и т.д. Для 1-го преобраз. коэф. ищем по ф-ле:
![]() .
.
![]() .
где i,j=2,3…
.
где i,j=2,3…
Продолжая этот процесс на (n-1)-ом этапе прямого хода МГ приведём с-му к треугольному виду. Треугольная структура с-мы позволяет последовательно вычислять знач. неизвестных , начиная с последнего. Этот процесс наз. обратным ходом МГ.
![]() )
)
Числа, на которые проводится деление в МГ, наз. ведущими или главными элементами. Главный элемент - наибольший
эл-т в столбце (для исключения деления на нуль и уменьшая погрешность вычислений)
2)Lu-разложение.
Если все главные
миноры квадратной м-цы А отличны от нуля
=>![]() нижняя L
и верхняя U
треугольная м-цы, что A=LU.
Если э-ты диагонали одной из м-ц L
или U
–фиксир.(ненулевые), то такое разложение
единственно. u11=a11,…,u1n=a1n;
ln1u11=an1,
ln1u1n+
…+unn=ann.
нижняя L
и верхняя U
треугольная м-цы, что A=LU.
Если э-ты диагонали одной из м-ц L
или U
–фиксир.(ненулевые), то такое разложение
единственно. u11=a11,…,u1n=a1n;
ln1u11=an1,
ln1u1n+
…+unn=ann.
![]() . (где
i
. (где
i![]() j)
j)
![]() .
(где i>j)
.
(где i>j)
Заменяем A
в Ax=b
=>LUx=b
решаем с-му
![]() => сначала вычисляем y
из Ly=b
затем полученный результат подставляем
в Ux=y
и находим x.
=> сначала вычисляем y
из Ly=b
затем полученный результат подставляем
в Ux=y
и находим x.
3)Метод квадратного корня(М. Холецкого).
Пусть A-симметричная
м-ца (aij=aji).
Представляем её в виде A=![]() ,
где U=
,
где U=![]() реш. с-мы сводится к реш. 2-ух треугольных
с-м :
реш. с-мы сводится к реш. 2-ух треугольных
с-м :
![]() и нах. По ф-лам:
и нах. По ф-лам:
![]()
Замечание:
Вычислительные затраты на операции
умножения и деления в МГ- О(![]() )
, в МКК- О(
)
, в МКК- О(![]() )
)
2.Метод трехдиагональной матричной прогонки.
Все методы решения СЛАУ можно разбить на два класса: прямые и итерационные. Прямые методы - методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (поэтому прямые методы наз. ещё точными методами)
Мы рассматриваем численное решение таких СЛАУ, у которых число уравнений совпадает с числом вещественных неизвестных, причем предполагается наличие единственного решения, если существование и единственность не следует из каких-либо условий.
Итак, изучается вопрос о численном решении системы …(1) или иначе, векторно-матричных уравнений Ах=b. (1a) где b – вектор свободных членов x - вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а А - вещественная n*n-матрица коэффициентов данной системы. Эффективность способов решения системы (1) во многом зависит oт структуры и свойств матрицы А: размера, обусловленности, симметричности, заполненности (т.e. соотношения между числом ненулевых и нулевых элементов), специфики расположения ненулевых элементов в матрице и др.
Если м-ца А слабо заполнена, т.е. имеет немного ненулевых коэф. ищем реш. с-мы
bixi-1+cixi+dixi+1=ri
(2), где
i=![]() ;
b1=0,
dn=0.
– Трёхточечные разностные у-ия второго
порядка.
;
b1=0,
dn=0.
– Трёхточечные разностные у-ия второго
порядка.
![]()
![]() =
=![]()
Чтобы избавиться
от ненулевых эл-ов в поддиагональной
части м-цы с-мы, предположим, что
наборы чисел
![]() и
и
![]() (i=
).
(i=
).
![]()
Подставляем
![]() в (2) :
в (2) :
![]()
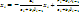 (3)
(3)
![]() ;
;
![]() (4)
(4)
Решение с-мы
сводится к нахождению прогоночных коэф.
,
по ф-лам (4) (прямая прогонка), а затем
получение неизв.
![]() по (3) (обратная прогонка).
по (3) (обратная прогонка).
Прогонка наз.
корректной, если знаменатели коэф.(4) не
обращаются в нуль, и устойчивой если
![]() <1
<1
![]() i
i
![]()
Если
![]() и
и
![]() у-ия (2) при i=2,...,n-1.
–отличны от нуля и
у-ия (2) при i=2,...,n-1.
–отличны от нуля и
![]() +
+![]() i=1,2,…,n
i=1,2,…,n
è![]() +
+![]() 0,
<1 , т.е. прогонка корректна и устойчива.
0,
<1 , т.е. прогонка корректна и устойчива.
Замечание:
Прямой метод даёт приближ. реш.
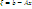 - невязка, по малости которой можно с
осторожностью судить о близости
найденного реш. к точному. Если
- невязка, по малости которой можно с
осторожностью судить о близости
найденного реш. к точному. Если
 -недостаточно мала, то следует искать
вектор-поправку p
:
-недостаточно мала, то следует искать
вектор-поправку p
:
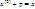 èAp=
èAp= Решаем 2
треугольные с-мы:
Решаем 2
треугольные с-мы:
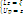 и прибавив найденную поправку p
к
и прибавив найденную поправку p
к
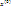 уточнённое приближение.
уточнённое приближение.Вычислительные затраты на операции умножения и деления О(5n) .
3. Итерационные методы решения СЛАУ.
ИМ-м., в котором точное реш. мб получено лишь в результате бесконечного повторения единообразных (как правило, простых) действий.
1)Метод простых итераций.
Дана с-ма Ax=b (1) , тем или иным способом преобразовывается в эквивалентную ей с-му:
x=Bx+c
(2), где B
и c
– некоторые новые м-ца и вектор
соответственно. Эту с-му можно трактовать,
как задачу о неподвижной точке линейного
отображения B
в пр-ве
![]() и по аналогии со скалярным случаем
определить посл-ть приближений
и по аналогии со скалярным случаем
определить посл-ть приближений
![]() к неподвижной точке
к неподвижной точке
![]() рекурентным р-ом :
рекурентным р-ом :
![]() ,
(3) k=0,1,2,…
- Итерационный процесс
,
(3) k=0,1,2,…
- Итерационный процесс
(3) , начиная с некот.
![]() T
–наз. МПИ.
T
–наз. МПИ.
Условия сходимости МПИ:
Условие, что все
собственные числа В по модулю меньше
1, явл. необх. и дост. для того чтобы
1)![]() 0,
при k
0,
при k![]() (k
(k![]() N)
N)
2)(E-B)- имела обратную (E-B)-1=E+B+B2+…+Bk+…
2. Если
![]() ,
то(E-B)
имеет обратную (E-B)-1=
,
то(E-B)
имеет обратную (E-B)-1=![]() и при этом справедливо нер-во:
и при этом справедливо нер-во:
![]()
Из 1. и 2. è
Т. Необход. и дост. усл. сх-ти МПИ при
нач. векторе
![]() к реш.
с-мы (2) явл. требование, чтобы все
собственные знач. м-цы В были по модулю
меньше 1.
к реш.
с-мы (2) явл. требование, чтобы все
собственные знач. м-цы В были по модулю
меньше 1.
Т. Пусть
![]() Тогда
начальном
МПИ сх-ся к единственному реш.
задачи (2) и
k
N
справедливы оценки погр.: 1)
Тогда
начальном
МПИ сх-ся к единственному реш.
задачи (2) и
k
N
справедливы оценки погр.: 1)
![]() – апостериорная.
– апостериорная.
2)
![]() –априорная.
–априорная.
Замечание:
1) Априорная оценка как правило, грубее апостериорной.
2)Априорная оценка
позволяет подсчитывать заранее число
итераций k
, достаточное для получения реш.
с заданной точностью
![]() .
Для этого нужно найти наименьшее целое
реш. нер-ва:
.
Для этого нужно найти наименьшее целое
реш. нер-ва:
![]() -относительно k
-относительно k
3)За обычно принимают вектор с - свободных членов (2) т.к. В “мала” è Bx “мал” è не должен сильно отличаться от с.
2)Метод Зейделя
МЗ – видоизменение МПИ реш. СЛАУ, приведенных к виду (2) при котором i-тые компоненты (k+1)-го приближения к искомому вектору используются уже найденные на этом, т.е. (k+1)-ом шаге , новые значения первых i-1 компонент. Это означает, что если с-ма Ax=b сведена к x=Bx+c, где В – матрица, с – вектор, то приближение к её реш. по МЗ определяется с-ой равенств :
![]() , где k=1,2…;
, где k=1,2…;
![]() -
э-ты нач. вектора.
-
э-ты нач. вектора.
МЗ называют м. последовательных смещений, а МПИ – одновременных смещений.
Условия сходимости МЗ и МПИ одинаковы. Область сходимости этих методов не всегда совпадают, а если и совпадают, то скорость сх-ти у МЗ больше. Достаточное условие сходимости МЗ не совпадает с дост. усл. сх-ти МПИ, но если МПИ сх-ся, то сх-ся и МЗ.
