9)Функция распределения случайной величины. Свойства. Графики разных типов.

Функцией распределения называют функцию F(X) , определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x , т.е. F(X)=P(X<x)

Геометрически это равенство можно истолковать так: F(X) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки x.

Свойства:

1.Значения функции распределения принадлежат отрезку [0,1]:

0 ≤ F(x) ≤ 1 Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.

2. F(x) —неубывающая функция, т.е F(x2) ≥ F(x1), если x2 > x1

3. Если возможные значения случайной величины принадлежат интервалу (a,b) то:

1) F(x) = 0 при x ≤ a

2) F(x) = 1 при x ≥ b

10)Математические ожидания случайной величины. Для чего нужно в экономике. Свойства.

Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.

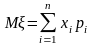
Свойства математического ожидания:

Математическое ожидание неслучайной величины с равно самой величине с:

M[c] = c.

Доказательствово: представим величину с как случайную величину, которая принимает одно и то же значение, с вероятностью р=1:

M[c]=c∙1=c.

2. При умножении СВ Х на неслучайную величину с не ту же самую величину увеличится ее математическое ожидание:

M[c×X] = c×M[X].

Доказательство:

3. При прибавлении к СВ Х неслучайной величины с к ее математическому ожиданию прибавляется такая же величина:

Доказательство: следует из свойств 1 и 3.

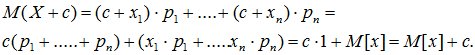
4.Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

M[X+Y] = M[X]+M[Y].

11)Дисперсия случайно величины. Для чего нужно в экономике. Свойства.

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины. Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

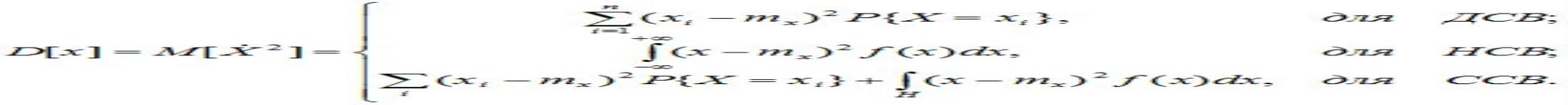
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.

Свойства дисперсии:

1. Дисперсия постоянной величины с равна нулю.

Доказательство:

2.При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.

D[X+c] = D[X].

Доказательство:

3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.

Доказательство:

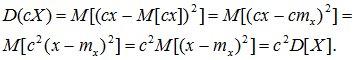
12)Нормальное распределение. Как задается. Основные характеристики. Где применяется в экономике.

Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид

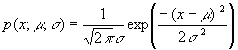где a = M(X) – математическое ожидание

б = б(X) - среднее квадратическое отклонение (б в кв.= D(X) - дисперсия).

График плотности распределения вероятности нормального закона называется нормальной кривой или кривой Гаусса: