11. Теорема Пуассона.

Теорема Пуассона: Между биномиальным распределением и распределением Пуассона имеется следующая связь: Пусть n  , p  0 и при этом np  a = const. Тогда:

Где .

Доказывается эта теорема с использованием второго замечательного предела (1-a/n)ⁿ  e^-a при n  .

Дискретная СВ Х с реализациями xk = k, k = 0, 1, …, имеет распределение Пуассона с параметром a > 0, что символически записывается как Х ~ П(а), если

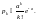
M[X] = D[X] = a.

 Эта теоре­ма дает пуассоновское приближение биномиального распределения и обычно используется при  p<0,1  и  npq 9

13.Функция распределения дискретной случайной величины, ее свойства и график

Для непрерывных случайных величин применяют такую форму закона распределения, как функция распределения. Функция распределения случайной величины Х, называется функцией аргумента х, что случайная величина Х принимает любое значение меньшее х (Х<х) F(х)=Р(Х<х) F(х) - иногда называют интегральной функцией распределения или интегральным законом распределения. Функция распределения обладает следующими свойствами:

1. 0<F(х)<1

2. если х₁>х₂,то F(х₁)>F(х₂)

3. 

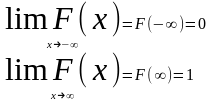
функция может быть изображена в виде графика. Для непрерывной величины это будет кривая изменяющееся в пределах от 0 до 1, а для дискретной величины - ступенчатая фигура со скачками.С помощью функции распределения легко находится вероятность попадания величины на участок от α до β Р(α<х<β)

рассмотрим 3 события

А - α<Х

В - α<Х<β

С - Х<β

С=А+В

Р(С)=Р(А)+Р(В)

Р(α<х<β)=Р(α)-Р(β)

Математическим-ожиданием Дисперсия

12.Локальная и интегральная теоремы Муавра-Лапласа.

Локальная

Если вероятность наступления события А в каждом из n независимых испытаний равна p (p0, p1), а число испытаний достаточно велико, то справедлива формула:

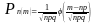
где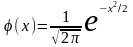 - малая функция Лапласа

Замечание: формула 2 исп, когда n10, np>10

Интегральная.

Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что в этих испытаниях событие А появится число раз, заключенное в границах [a;b], может быть посчитана по формуле:

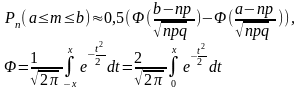Свойства функции Лапласа:

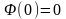
Функция нечетная, возрастающая

X>4, Ф(х)=1 Следствие из интегральной теоремы Муавра-Лапласа. Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянно и отлично от нуля и единицы, то вероятность того, что число появлений события А отклонится от произведения np не больше, чем на некоторое положительное число r по модулю, может быть посчитано по формуле

14. Дискретные случайные велечины. Закон распределения, Биноминальное, геометричиское, распределение Пауссона.

Определение. Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами npq, если она принимает значения 0, 1, 2,..., m,... ,n с вероятностями

,

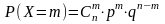где 0<р<l, q=1-p.

Как видим, вероятности Р(Х=m) находятся по формуле Бернулли, следовательно, биномиальный закон распределения представляет собой закон распределения числа Х=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Ряд распределения биномиального закона имеет вид:

Очевидно, что определение биномиального закона корректно, т.к. основное свойство ряда распределения выполнено, ибо есть не что иное, как сумма всех членов разложения бинома Ньютона:

Математическое ожидание случайной величины Х, распределенной по биноминальному закону,

а ее дисперсия

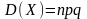
Определение. Дискретная случайная величина Х имеет закон распределения Пуассона с параметром λ > 0, если она принимает значения 0, 1, 2,..., m, ... (бесконечное, но счетное множество значений) с вероятностями ,

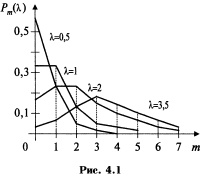
Ряд распределения закона Пуассона имеет вид:

Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения выполнено, ибо сумма ряда .

На рис. 4.1 показан многоугольник (полигон) распределения случайной величины, распределенной по закону Пуассона Р(Х=m)=Р_m(λ) с параметрами λ = 0,5, λ = 1, λ = 2, λ = 3,5.

Теорема. Математическое oжидaниe и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.

и

15.Математическое ожидание дискретн случайной величиныи его св-ва. Математическим ожиданием случайной величины х (M[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности появления тех или иных значений. Для дискретной случайной величины

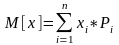
Для непрерывной

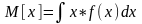
С механической точки зрения мат. Ожидание это абсцисса центра тяжести системы точек расположенных по одноименной оси. Размерность мат. Ожидания совпадает с размерностью самой случайной величины. Математическое ожидание случайной величины всегда больше наименьшего значения и меньше наибольше