34. Эмпирическая функция распределения и её основные свойства.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения x относительную частоту события X< x. Итак, по определению, , где – число вариантов, меньших x; n – объём выборки.

Свойства: 1) Значения эмпирической функции принадлежат отрезку [0,1].

2) – неубывающая функция.

3) если – наименьший вариант, то если – наибольший вариант, то , при .

35. Статистическая оценка неизвестных параметров распределения. Виды оценок.

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Виды: несмещённая, смещённая, эффективная, состоятельная.

36. Классификация точечных оценок (состоятельные, несмещённые, эффективные).

Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру.

Несмещённой называют статистическую оценку 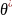, математическое ожидание которой равно оцениваемому параметру при любом объёме выборки, т.е. .

Эффективной называют статистическую оценку, которая (при заданном объёме выборки n) имеет наименьшую возможную дисперсию.

37.Выборочное среднее и свойство устойчивости среднего.

Выборочным средним называют среднее арифметическое значение признака выборочной совокупности. Если все значения , , …, признака выборки объёма n различны, то

. Если же значения признака , , …, имеют соответственно частоты , , …, , причём + +…+ =n, то , .

При увеличении объёма выборки n выборочное среднее стремится по вероятности к генеральному среднему, а это означает, что выборочное среднее есть состоятельная оценка генерального среднего. Из сказанного следует также, что если по нескольким выборкам достаточно большого объёма из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит свойство устойчивости выборочных средних.

38. Выборочная оценка дисперсии. Несмещённая оценка дисперсии.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений наблюдаемых значений признака от их среднего значения .

Если все значения , , …, признака выборки объёма n различны, то .

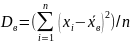Если же значения признака , , …, имеют соответственно частоты , , …, , причём + +…+ =n, то .

Исправленная дисперсия является несмещённой оценкой генеральной дисперсии:

.

39. Доверительная вероятность оценки и доверительный интервал. Надёжностью (доверительной вероятностью) оценки Ѳ по Ѳ* называют вероятность γ, с которой осуществляется неравенство . Обычно надёжность задаётся наперёд, причём в качестве γ берут число, близкое к единице. Наиболее часто задают надёжность, равную 0,95, 0,99 и 0,999.

Доверительным называют интервал (Ѳ*-δ, Ѳ*+δ), который покрывает неизвестный параметр с заданной надёжностью γ.

40. Доверительные интервалы для математического ожидания СВ, имеющей нормальный закон распределения. Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение  этого распределения -. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью . Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки  к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением . Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами  .Потребуем, чтобы выполнялось равенство   Заменив Х и «сигму», получим

Получим

41. Критерий согласия X²  Критерий согласия хи-квадрат используется для проверки гипотезы о совпадении эмпирического и теоретического (постулируемого) распределений дискретных случайных величин. Критерий основывается на сравнении наблюденных и ожидаемых (теоретических) встречаемостей. Статистика критерия равна сумме квадратов разностей между наблюденными и ожидаемыми встречаемостями, деленных на ожидаемые встречаемости:

Хи-квадрат сравнивает нашу теорию с практикой. Если получилась большая выборка, оформляем в виде интервального статистического ряда и строим гистограмму. Гистограмма показывает нам гипотезу о законе распределения. Хи-квадрат сравнивается с критической. Если хи-квадрат < критической, то принимаем гипотезу. Но иногда это обман. Мы можем выбрать неправильную гипотезу, а хи-квадрат покажет, что это верная гипотеза.

42. Метод наименьших квадратов.— один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.