1. Элементы комбинаторики: размещения, перестановки, сочетания. Привести примеры.

Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 1. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1,2), (2,1), (1, 3), (3,1), (2,3),(3,2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначается  и вычисляется по формуле:

Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 2. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}. Число сочетаний обозначается 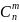и вычисляется по формуле:

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 3. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначается  и вычисляется по формуле

2. Случайный эксперимент. Основные особенности. Привести пример. Случайным экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз.

Основные особенности: множественность исходов, непредвиденность результата, многократность повторения (при одних и тех же условиях), наличие определённых закономерностей при многократном повторении.

Примеры случайного эксперимента: подбрасывание монеты, извлечение одной карты из перетасованной колоды.

3. Случайные события. Виды случайных событий. Действия над событиями. Полная группа событий. Противоположные события. Результат (исход) испытания называется случайным событием (или просто: событием).

Виды событий: Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными.

Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.

Событие называется невозможным, если оно не может произойти в условиях данного опыта. Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться.

События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Введем понятие противоположного, или дополнительного, события. Под противоположным событием   понимается событие, которое обязательно должно произойти, если не наступило некоторое событие  . Противоположные события несовместны и единственно возможны. Они образуют полную группу событий.

Действия над событиями:

Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

4. Классическое определение вероятности. Привести пример. Вероятность события   равна отношению числа случаев  , благоприятствующих ему, из общего числа   единственно возможных, равновозможных и несовместных случаев к числу  , т. е.

( .)

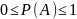Пример вопросу №4. Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4 бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди выбранных ламп будут 2 бракованные?

5 . Геометрическая вероятность. Привести пример. Пусть на плоскости задана некоторая область   площадью  , в которой содержится другая область  площадью   (рис. 3). В область   наудачу бросается точка. Чему равна вероятность того, что точка попадет в область  ? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области  , и вероятность попасть в какую-либо часть области   пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область   при бросании наудачу точки в область 

Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.

6. Относительная частота. Устойчивость относительной частоты. Статистическая вероятность. Пусть произведено n испытаний, при этом некоторое событие А наступило m раз. Число m называется абсолютной частотой (или просто частотой) появления события А, а отношение ω(A)=m/n называется относительной частотой появления случайного события А в данной серии опытов. С увеличением числа испытаний в сериях относительная частота приближается к некоторому числу Р(А), стабилизируясь возле него и принимая всё более устойчивые значения.

Статистической вероятностью события А называется число Р(А), около которого группируются значения относительной частоты события А при большом числе опытов (испытаний).