2. Физические процессы, лежащие в основе электростимулированной миграции ионов

Прежде чем приступить к рассмотрению процессов, имеющих место при проведении электростимулированной миграции ионов из расплава соли в стеклянную подложку, необходимо определить влияние структуры стекла на саму возможность диффузии ионов.

В основе структуры силикатного стекла, т.е. стекла, содержащего в качестве основного компонента кремнезем, лежат ионы (SiO₄)^{4 -} , образующие тетраэдры, в центре которых располагается малый ион Si⁴⁺ радиусом 0,039 нм, а в вершинах находятся более крупные ионы O^2– , имеющие радиус 0,132 нм. Расстояние от центра тетраэдра до центра ионов O^2– составляет 0,162 нм, а между соседними ионами O^2– – 0,265 нм. На рис. 10 представлен внешний вид такого тетраэдра.

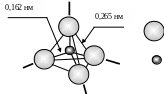
– ион O^2–

– ион Si⁴⁺

Рис. 10. Внешний вид тетраэдра (SiO₄)^{4 -}

Соединяясь друг с другом вершинами, эти тетраэдры образуют непрерывную в одном, двух или трех измерениях пространственную структуру. Взаимным расположением тетраэдров в структуре, их упорядоченностью определяются основные свойства материала. Правильно упорядоченные тетраэдры образуют правильную кристал -лическую решетку, характерную для кристаллического кварца (рис. 11а), что предопределяет анизотропность его свойств. В то же время в кварцевом стекле (плавленом кварце) наблюдается неупорядоченное расположение тетраэдров (рис. 11б) и изотропность свойств наряду с отсутствием ярко выраженной температуры плавления, присущей кристаллическим материалам.

а б

Рис. 11. Кристаллическая решетка кристаллического (а)

и плавленого (б) кварца

В общем случае в центре кислородных тетраэдров могут находиться и другие стеклообразователи (B, P, Ge), при этом стекла носят названия боратных, фосфатных или германатных [54–56].

Как правило, большое число таких тетраэдров (многогранников) имеют общие вершины, занятые так называемыми мостиковыми ионами кислорода. Ионы кислорода, принадлежащие лишь одному полиэдру, называются «немостиковыми» ионами кислорода. В промежутках структурной сетки могут находиться некоторые положительные ионы (преобразующие сетку), например: Li⁺, Na⁺, K⁺, Ba²⁺, Ca²⁺, Mg²⁺. Эти катионы, не способные самостоятельно образовывать непрерывную структурную сетку, называются модификаторами. Катионы модификаторов располагаются в свободных полостях структурной сетки, компенсируя избыточный отрицательный заряд сетки, обусловленный наличием «немостиковых» ионов кислорода. Кислородное окружение катионов модификаторов формируется в соответствии с их координационными требованиями. Прочность связи модификатор – кислород значительно ниже прочности связи стеклообразователь – кислород, поэтому модификаторы не образуют прочных координационных групп. Так, например, прочность связи кислорода с кремнием равна 443 кДж/моль, а прочность связи кислорода с натрием равна 84 кДж/моль, с калием – 54 кДж/моль. Структурная сетка натрий-силикатного стекла ­­ более рыхлая и менее связанная, чем сетка кварцевого стекла, в ней крупнее промежутки и полости, в которых располагаются ионы натрия (рис. 12).

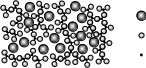
– ион Na⁺

– ион О^2

– ион Si⁴⁺

Рис. 12. Структурная сетка натрий-силикатного стекла

Структурную сетку стекла часто характеризуют следующими величинами: R – среднее число ионов кислорода на один образующий структурную сетку ион; X – среднее число «немостиковых» ионов кислорода на полиэдр;

Y – среднее число «мостиковых» ионов кислорода на полиэдр.

Если ограничиться рассмотрением силикатных стекол, которые имеют лишь тетраэдры кислорода, то будут справедливы следующие соотношения:

X + Y = 4. (1)

X + Y = R. (2)

Откуда

X = 2R – 4. (3)

Y = 8 – 2R. (4)

У плавленого кварца все ионы кислорода – «мостиковые» (R = 2, Y = 4). Поэтому он имеет жесткую сетку. Атом кремния в кварце окружен четырьмя атомами кислорода, расположенными симметрично в вершинах тетраэдра. Тетраэдры не образуют в пространстве геометрически правильных соединений, характерных для решеток кристаллических модификаций кварца. Несмотря на это, плавленый кварц обладает довольно «плотной» структурой по сравнению со стеклами, имеющими более низкие значения Y. Структуры кристаллического и плавленого кварца не являются плотноупакованными, так как тетраэдры соединяются вершинами, а не ребрами и не гранями. В кварцевом стекле имеются свободные структурные полости, ограниченные в пространстве «мостиковыми» ионами кислорода.

Если в структурную сетку SiO₂ ввести некоторое количество окиси металла, например Na₂O, то определенное число «мостиковых» ионов кислорода будет замещено таким же числом пар «немостиковых» ионов кислорода, что приведет к уменьшению Y. Вследствие этого структурная сетка стекла становится менее прочной, степень сцепления сетки уменьшается, а сетка при этом разрыхляется. Это значит, что промежутки между тетраэдрами, а также «окна» между ними увеличиваются, что способствует довольно легкой диффузии ионов различных, чаще всего щелочных, металлов в стекло.

Диффузия происходит за счет разности концентраций диффундирующих веществ. Так если у поверхности стекла концентрация ионов какого-либо щелочного металла С_0, а в стекле С = 0, то эти ионы будут диффундировать в направлении их меньшей концентрации, т.е. в стеклянную подложку.

Математическое описание диффузионных процессов было сделано в 1855 г. немецким ученым А.Фиком в виде двух законов, основанных на уравнениях теплопроводности.

Уравнение, характеризующее скорость диффузии атомов одного вещества в другое при постоянном во времени потоке этих атомов и градиенте их концентрации, носит название первого закона Фика.

, (5)

где – вектор плотности потока атомов вещества; D – коэффициент пропорциональности, или коэффи­циент диффузии; – вектор градиента концентрации диффундирующих атомов [57].

Коэффициент диффузии D определяет плотность по­тока атомов диффундирующего вещества при заданном градиенте концентрации. Так как диффузионный поток атомов вещества идет в направлении выравнивания пе­репада концентрации, то коэффициент диффузии D явля­ется мерой скорости, с которой система способна при за­данных условиях выравнять разность концентраций, и имеет размерность (см²/с). Эта скорость зависит только от подвижности диффундирующих атомов в мат­рице стекла. Коэффициент диффузии существенно зави­сит от температуры. Чем выше температура, тем больше энергия диффундирующих атомов и их скорость в кри­сталлической решетке стекла. Эта зависимость выража­ется уравнением Аррениуса

, (6)

где D₀ – постоянная, имеющая размерность (см²/с) и зависящая от структуры стекла, размеров и валентно­сти диффундирующих ионов и других параметров, оп­ределяющих процесс диффузии, т.е. кажущийся коэф­фициент диффузии при Т , который не зависит от температуры и определяется экспериментально в каж­дом конкретном случае; Е – энергия активации, т.е. энергия, необходимая атому для диффузии; k – посто­янная Больцмана; Т – абсолютная температура.

Градиент концентрации С при объемной диффу­зии имеет три составляющих по координатным осям. Однако если глубина диффузии значительно меньше поперечных размеров площади, через которую она про­исходит, то мы вправе рассматривать процесс диффузии как одномерный, т.е. направленный нормально к по­верхности подложки. При этом первый закон Фика примет вид

. (7)

Из закона сохранения массы следует, что изменение во времени C(x, t) равно отрицательному приращению потока J.

, (8)

откуда следует второй закон Фика

. (9)

Второй закон Фика определяет скорость изменения концентрации диффундирующих атомов в любой плос­кости, перпендикулярной направлению диффузии. В случае, если С мало, а D является постоянной величиной, второй закон Фика принимает вид

. (10)

Это уравнение имеет несколько решений в зависи­мости от граничных условий. На практике чаще всего рассматриваются два случая диффузии: диффузия из бесконечного источника и диффузия из конечного ис­точника внедряемых атомов.

Под бесконечным (постоянным) источником понимают такое состояние системы, когда количество ато­мов, уходящих из приповерхностного слоя подложки в ее объем, равно количеству атомов, поступающих в приповерхностный слой. Таким является источник с бесконечно большим содержанием атомов, которые в нем имеют существенно более высокие скорости, чем в подложке. Начальное и граничное условия в этом слу­чае записываются следующим образом:

C(x, t) = 0 при x  0, t = 0,

C(0, t) = C_s при x = 0, t  0, (11)

C(, t) = 0 при x  , t  0.

Здесь x – расстояние, измеряемое вглубь от поверх­ности подложки; x = 0 – координата поверхности, через которую происходит диффузия; C_s – приповерхностная концентрация диффундирующих атомов, поддерживае­мая постоянной в течение всего процесса; C(x, t) – кон­центрация атомов на любой глубине подложки и в лю­бое время; t – время диффузии.

При этих условиях решение уравнения второго за­кона Фика имеет вид

, (12)

где  – переменная интегрирования.

Второй член в квадратных скобках представляет собой выражение функции ошибок, поэтому последнее уравнение можно записать следующим образом:

, (13)

или

, (14)

где erfc – символ, означающий дополнение функ­ции ошибок до единицы.

Э та формула описывает распределение концентра­ции диффузанта в стеклянной подложке в зависимости от глубины проникновения и времени процесса в слу­чае, если диффузия проводится из неограниченного ис­точника. Графическое представление этого распределе­ния приведено на рис. 13.

Рис. 13. Распределение концентрации диффузанта по

глубине при проведении диффузии из

неограниченного источника

Данный вид диффузии (диффузии из неограничен­ного источника) имеет место в том случае, если стек­лянная подложка приводится в соприкосновение с расплавом соли, содержащим диф­фундирующие ионы, и при этом наиболее подвижные ионы стекла обмениваются на ионы расплава.

При проведении диффузии из ограниченного ис­точника, что наблюдается при твердотельной диффузии из тонкой металлической пленки, нанесенной на по­верхность подложки, поверхностная концентрация диффузанта меняется с течением времени. При этом на­чальные условия таковы:

при 0  x  d

при x  d. (15)

С учетом этих начальных условий решение уравне­ния второго закона Фика имеет вид

, (16)

где Q – общее количество внедренных в подложку атомов в любой момент времени.

Это уравнение представляет собой функцию рас­пределения (закон) Гаусса и показывает распределение концентрации диффузанта в зависимости от глубины и времени (рис.14).

Рис. 14. Распределение концентрации диффузанта по

глубине при проведении диффузии из

ограниченного источника

Максимальное значение приповерхностной концен­трации C_s ограничивается предельной концентрацией наиболее подвижных ионов стекла, участвующих в процессе ионного обмена (Li⁺, Na⁺, K⁺), в случае прове­дения диффузии из неограниченного источника, т.е. из расплава соли. Если же диффузия проводится из метал­лической пленки, то C_s будет ограничиваться пределом растворимости диффундирующих ионов в матрице стекла.

Диффузия ионов при наличии стимулирующего электрического поля описывается следующим уравнением:

, (17)

где – подвижность ионов в стекле; Е – напряжен­ность электрического поля [58].

Решение этого уравнения для граничных условий С(x, 0) = 0 при х  0 и С(0, t) = С_s при t  0 имеет вид

. (18)

Если пренебречь вкладом от процесса тепловой диф­фузии, то в случае проведения электростимулированной миграции ионов из неограниченного источника распределение концентра­ции внедренных в стекло ионов приобретает ступенча­тый характер (рис. 15). Здесь же пунктиром показано распределение концентра­ции внедренных в стекло ионов при отсутствии электрического поля.

0

Рис. 15. Распределение концентрации диффузанта по глубине при проведении электростимулированной миграции

из неограниченного источника

Поскольку в процессе электростимулированной ми­грации ионов в стеклянной подложке происходит изме­нение химического состава, то и показатель преломле­ния в области диффузии также претерпевает изменение  . Отсюда следует, что профиль изменения по­казателя преломления имеет в этом случае ступенчатую форму, что и подтверждается многочисленными экспе­риментами.