6. Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.

Коэффициент оптимизма λ выбирается между 0 и 1, при этом если коэффициент равен 1, то критерий Гурвица превращается в критерий Вальда (по пессимизму результата), если коэффициент равен 0, то в критерий Севиджа.

Число (1- λ) будет характеризовать меру пессимизма игрока А, поэтому в данной работе будем называть коэффициентом пессимизма. Таким образом коэффициенты оптимизма и пессимизма в сумме дают единицу. С увеличением меры ответственности коэффициент λ стремится к нулю: чем серьезнее последствия ошибочных решений, тем больше желание ЛПР перестраховаться. А чем ближе λ к нулю, тем ближе (1- λ) к единице, т.е. тем больше пессимизма. И наоборот. Заметим, что при коэффициенте λ=0,5 видно нейтральность игрока в оценивании ситуации при выборе стратегии.

λ₁, λ₂,…, λ_n – числовые коэффициенты количественно характеризующие субъективную оценку игрока А в играх с природой. Такое положение делает обобщенный критерий Гурвица в большей степени субъективным, чем объективным. На результат выбора данной стратегии могут влиять различные ситуации, при которых известны возможные выигрыши.

Существуют некоторые методы выбора данных коэффициентов. Так Лабскер предлагает математико-формализованный метод, для ограничения степени полного произвола субъективного выбора игрока А, который будет разобран ниже.

В.Б. Волгоградский предлагает иной подход к выбору коэффициентов, который состоит в том, что игрок А сначала субъективно определяет числовое значение показателя своего оптимизма λ_о [0,1], а затем в зависимости от этого значения определяет коэффициенты λ_j, j=1,2,…,n, по следующей формуле:

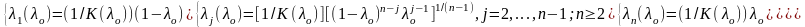(5.1)

Матиматико-формализованный подход Лабскера выбора коэффициентов λ зависит от средних выигрышей и носит менее субъективный характер, чем модель, предложенная Волгоградским. Её суть заключается в следующем:

Рассматривается игра с природой размером mxn, в которой матрица А является матрицей выигрышей игрока А, матрица B – матрица ранжированных выигрышей. Считается, что все выигрыши положительные. Далее используется специальная формула в зависимости от ситуации (думаю формулу учить не надо):

(5.2)

Где λ_о – показатель оптимизма, λ_P – показатель пессимизма;

b – сумма всех выигрышей матрицы, b^-1 необходимо для выведения среднего значения выигрышей j-го ранга;

- сумма выигрышей b_ij j-го ранга; λ _j = b _j / b – выражение коэффициентов λ_j через выигрыши.

6. Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.

Весь выигрыш Игрока зависит от того, какой коэффициент оптимизма он выберет. Он может рискнуть и попробовать выиграть большую сумму, а может не рисковать и с уверенностью выиграть меньшую сумму. Таким образом игрок может быть пессимистом, крайним оптимистом или нейтралом.

Коэффициент оптимизма λ выбирается между 0 и 1, при этом если коэффициент равен 1, то критерий Гурвица превращается в критерий Вальда (по пессимизму результата), если коэффициент равен 0, то в максимаксный – то есть игрок будет крайним оптимистом.. Число (1- λ) будет характеризовать меру пессимизма игрока А, поэтому в данной работе будем называть коэффициентом пессимизма. Таким образом коэффициенты оптимизма и пессимизма в сумме дают единицу.

С увеличением меры ответственности коэффициент λ стремится к нулю: чем серьезнее последствия ошибочных решений, тем больше желание ЛПР перестраховаться. А чем ближе λ к нулю, тем ближе (1- λ) к единице, т.е. тем больше пессимизма. И наоборот. Заметим, что при коэффициенте λ=0,5 видно нейтральность игрока в оценивании ситуации при выборе стратегии.