• Күш. Табиғаттағы заттық денелер әрдайым өзара немесе қоршаған ортамен әсерде болады.

Күшдеп денелердің өзара механикалық әсерлерінің өлшемін атайды. Күнделікті тұрмыста, техника саласында күштің денеге әсері оның шамасы (модулі), бағыты және түсу нүктесі арқылы анықталатынын көреміз. Бұдан күшті векторлық шама деп қарастыруға болатындығы шығады.

Физикадан белгілідей күш шамасы динамометрдің жәрдемімен өлшенетін салмақ арқылы анықталады.

Механикада күштің өлшем бірлігі ретінде физикалық шамалардың өлшеу бірліктерінің халықаралық системасынада (СИ) 1 Ньютон алынады.

Ньютон деп массасы 1 кг денеге күш әсері бағытында 1м/с² үдеу беретін күш аталады. Ньютонның еселік бірліктері – килоньютон (1кН = 10³Н) және меганьютон (1МН = 10⁶Н).

Күшті кез келген вектор сияқты бағытталған кесіндімен бейнелеуге болады. Вектор - тың АВ кесінді ұзындығы (I.1.1- сурет) белгілі бір масштабта алынған сан мәнін (модулін) бейнелейді, ал оның бағыты күштің әсер ету бағытына дәл келеді. Ол вектордың бас нүктесі А күштің денеге әсер ететін нүктесіне сәйкес болады. Дененің күш әсер етіп тұрған А нүктесі күштің түсу нүктесі деп, ал бойымен күш векторы бағытталған сызығын күштің әсер ету сызығыдеп атайды.

Қандай да бір денеге бір мезгілде әсер ететін күштер жиынын күштер жүйесі деп атайды.

Күштер жүйесі дөңгелек жақшалар ішінде алынған күш векторларымен белгіленеді. Мысалы: - күштен тұратын күштер жүйесі.

Дененің механикалық күйін өзгертпей әсер етуші күштер жүйесін тепе–теңдіктегі күштер жүйесі деп немесе нөлге эквивалентті (пара-пар) күштер жүйесі деп атайды

Денеге бірдей механикалық әсер етуші әр түрлі күш жиындары бір-біріне эквивалент жүйелер деп аталады.

Эквивалент екі күштер жүйесінің қандай да болмасын бір денеге әсерлері бірдей болғандықтан, олардың біреуін екіншісімен алмастыруға болады.

Қатты денеге түсірілген күштер жүйесі бір күшке эквивалент болса, онда ол күшті берілген күштер жүйесінің тең әсерлі күшідеп атайды

Берілген күштер жүйесінің теңестіруші күші осы жүйенің теңгеруші күші деп аталады.

• Статиканың аксиомалары. Дененің тепе-теңдікте болу шарттары өмірлік тәжірибеден негізделген және дәлелдеусіз қабылданатын бірнеше жағдайға негізделіп қорытылады.

Оларды статиканың аксиомалары деп атайды.

Статиканың негізгі аксиомалары ағылшын ғалымы Ньютон (1642-1727) тұжырымдаған, сондықтан да олар ғалымның атымен аталады.

1 - аксиома(екпін аксиомасы немесе Ньютонның бірінші заңы).Қандай да болмасын күштер мәжбүр етпесе, дене тыныштықтағы немесе бірқалыпты түзу сызықты қозғалыстағы күйін сақтай алады.

Екпін немесе екпіндік деп, қозғалыстағы заттық дененің күш әсері болмаса да қозғалысын сақтайтын немесе күш әсерінен қозғалысын біртіндеп өзгертетін мүмкіндігін атайды.

2 - аксиома(екі күштің тепе-теңдік шарты).Екі күш түскен еркін қатты дене тепе-теңдігі үшін, күштердің шамалары (модульдері) тең және әсер сызықтары бір болып қарама-қарсы бағытталуы қажет және жеткілікті, яғни , егер және (I.1.9 - сурет).

Басқаша айтқанда, екі күш тепе-теңдікте болу үшін, олардың модульдері тең болуы және бір түзу бойымен қарама–қарсы бағытталуы қажет және жеткілікті.

3 - аксиома(теңестірілген күштерді қосу не алып тастау, шығару принципі).Кез келген күштер жүйесіне нөлге эквивалент күштер жүйесіне қосқаннан немесе алып тастағаннан (шығарғаннан) берілген жүйенің қатты денеге жасайтын әсері өзгермейді.

Егер және екі күштер жүйесі болса, онда бұл аксиома былай жазылады

4 - аксиома(параллелограмм ережесі). Қатты дененің бір нүктесіне түсірілген екі күштің тең әсерлі күшін,ің шамасы мен бағыты берілген күштерден құрылған параллелограмм диагоналымен анықталады да, сол нүктеге түсіріледі.

Қабырғалары берілген векторлар болатын параллелограмм диагоналын тұрғызуды (I.1.10, а - сурет) векторлық немесе геометриялық қосу деп атайды. Демек, бір нүктеге түсірілген екі күштің тең әсерлі күші осы күштердің векторлық қосындысына тең

және сол нүктеге түсіріледі.

Күш параллелограммен қатар екі жүйенің тең әсерлі күшін, күш үшбұрышымен де анықтауға болады. (I.1.10, b - сурет). Тең әсерлі күштің шамасы I.1.10, b, c - суреттерінен көрінетіндей векторлардың қосылу тәртібіне байланысты емес, яғни

5 – аксиома (әсер және қарсы әсер заңы).Екі дене бір–біріне әрқашан модульдері тең, бір түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді.

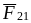Бұл аксиома физикада Ньютонның үшін,ші заңы деп аталады. Бесінші аксиома механикада өте маңызды орын алады. Егер денесі денесіне күшімен әсер етсе, денесі денесіне дәл осы сияқты модульді күшімен қарама-қарсы бағытта әсер етеді (I.1.11 - сурет). және күштерінің модульдері тең, ал бағыттары бір түзу бойымен қарама-қарсы бағытталса да, олар әр денеге түсірілгендіктен тепе-теңдіктегі күштер жүйесін құра алмайды. Бұл күштердің бірін тура әсер етуші күш деп қараса, екіншісі қарсы әсер күш болып табылады. Сонымен аксиома бойынша әрбір әсерге оған тең және қарама-қарсы бағытталған қарсы әсер болады. Осыдан барып табиғатта сыңар күш болмайтыны, әрбір күшке үнемі онымен бірге екінші бір қарама-қарсы күш сәйкес келіп отыратыны байқалады.

6 – аксиома (қатаю ережесі).Деформацияланатын дене абсолют қатты денеге айналса да механикалық күйі өзгермейді.

Басқаша айтқанда, берілген күштер жүйесі әсерінде тұрған деформацияланатын дене тепе-теңдігі, егер дене мезетте қатайса да, яғни абсолют қатты денеге айналса да өзгермейді.

Бұл ережеден абсолют қатты дененің тепе-теңдігінің қажет және жеткілікті болатын шарттарының деформацияланатын дене тепе-теңдігі үшін тек қажетті ғана болып, жеткілікті болмайтындығы көрінеді. Мысалы, егер күштер әсеріндегі резенкеден жасалған дене оның тепе-теңдігі дене абсолют қатты денеге айналса да сақталады. Ал бірақ та күштер тепе-теңдікте тұрған абсолют қатты дене бірден резенкеден жасаған денеге айналса, онда дене тепе-теңдік күйін сақтай алмауы мүмкін.

• Статиканың қарапайым теоремалары. Күшті әсер сызығы бойымен көшіру теоремасы.Кез келген күшті, әсер ететін дененің механикалық күйін өзгертпей-ақ өзінің әсер сызығы бойымен басқа нүктеге көшіруге болады.

күші қатты дененің нүктесіне түсірілген, осы күшті әсер сызығы бойындағы қандай да бір нүктесіне көшіру қажет делік (I.1.12, а - сурет). күшін,ің әсер сызығы бойымен нүктесіне өзара тең, қарама-қарсы бағытталған және күштерін түсірейік (I.1.12, b - сурет). Бұл күштердің шамасы берілген күшінің шамасына тең болсын және

_{сондықтан да} нүктесіндегі екі күш нөлге эквивалент болатын жиын құрайды, онда

Үшінші аксиома бойынша Соңғы үш күштен тұратын жүйеде және күштері екінші аксиома бойынша

Олай болса, үш күштен тұратын жүйеден оларды алып тастауға болады.

Бұл дегеніміз нүктесіне түсірілген күшін, әсер сызығы бойынша нүктесіне көшірілгенмен пара-пар (I.1.12, с - сурет). Теорема дәлелденді.

Сонымен, денеге әсер ететін күшін, өзінің әсер ету сызығының бойымен кез келген нүктеге көшіруге болады.

Әсер сызығы бойынша көшіруге болатын векторларды сырғыма векторлар деп атайды. Демек қатты денеге әсер етуші күштер де сырғыма векторлар болып табылады.

Үш күш туралы теорема.Егер бір-біріне параллель емес, бір жазықтықта жататын үш күш тепе-теңдіктегі күштер жиынын құрайтын болса, онда күштердің әсер сызықтары бір нүктеде қиылысады.

Қатты дененің нүктелерінде бір жазықтықта жатқан, өзара параллель емес күштері берілсін делік (I.1.13 - сурет) және күштерінің әсер сызықтары бір нүктеде қиылысатын болсын. және күштерін әсер сызықтары бойымен нүктесіне көшіріп, параллелограмм ережесі бойынша осы күштердің тең әсерлі күшін, анықтайық

Олай болса,

_{Теорема шарты бойынша}

Сондықтан,

Екінші аксиомаға сәйкес, екі күштің тепе-теңдікте болуы үшін олар бір түзудің бойымен қарама-қарсы бағытталулары қажет. Олай болса үшінші күштің де әсер сызығы нүктесінен өтуге тиісті. Сонымен теорема дәлелденді.

• Күштің өске проекциясы. Белгілі бағытталған түзу сызықты өс деп атайды. Күштің өске проекциясы деп, күш векторының ұштарынан өске түсірілген екі перпендикулярмен шектелген, өстің бағытталған кесіндісі аталады. Егер кесінді бағыты өстің оң бағытымен сәйкес келсе, күштің өске проекциясы оң таңбалы деп есептеледі. Егер кесінді бағыты өстің оң бағытына қарама-қарсы болса, күштің өске проекциясы теріс таңбалы делінеді.

күші мен өсі берілген делік (I.1.3, а - сурет). күшін,ің өсіне проекциясы кесіндісімен кескінделген және проекциясы оң таңбалы.

I.1.3, а - суретте көрсетілгендей, , ал ұшбұрышынан , олай болса

. (I.1.1)

Сонымен, күштің өске проекиясының шамасы осы күштің модулін өстің оң бағыты мен күштің бағыты арасындағы бұрыш косинусына көбейткенге тең.

(I.1.1) өрнегі, егер күш пен өстің оң бағыты арасындағы бұрыш сүйір болса, күштің проекциясы оң таңбалы болатынын көрсетеді.

Егер күш векторының өстің оң бағытымен жасайтын бұрышы доғал болса, күштің проекциясы теріс таңбалы болады, яғни болса, онда (I.1.3, b - сурет)

Егер күш берілген өске параллель болса, онда оның проекциясы сәйкес таңбамен алынған күштің модуліне тең (I.1.3, c, d – сурет), яғни

Егер күш берілген өске перпендикуляр болса, онда оның проекциясы нөлге тең (I.1.3, e – сурет), яғни

жазықтықтың А нүктесіне түсірілген күшін, және өстеріне проекциялайық. күші мен оның және проекциялары I.1.4 - суретте көрсетілген

; .

Күштің және проекциялары өзара перпендикуляр болғандықтан, егер күштің екі проекциясының шамалары белгілі болса, күштің модулі мен күш векторының бағытын анықтауға болады. Ол үшін, үшбұрышын қарастырсақ, онда күштің модулі

. (I.1.2)

Ал күштің бағыттаушы косинустары

; . (I.1.3)

күшін, координата өстеріне параллель екі және күштерінің тең әсерлі күші іспетті қарастыруға болатынын атап өтуге болады (I.1.4 - сурет). күшін,ің құраушы күштері пен векторлық шама болып, күштің проекциялары пен алгебралық шама болғандықтан, күштің құраушылары мен проекциялары бір-бірінен айрықша ерекшеленеді.

• Күш моменті.Күштің нүктеге қатысты моменті. Тұрмыста белгілідей, қатты дене өзіне түсірілген күш әсерінен тек ілгерілей қозғалып қоймай, сонымен қатар белгілі бір нүктеге қатысты айнала да қозғалады. Күштің денеге айналдырушы әсері күш моменті деген ұғыммен сипатталады.

Күштің нүктеге қатысты моменті деген ұғымды механикаға енгізген қайта өрлеу дәуірінің италяндық ғалым және суретші Леонардо да Винчи (1452-1519).

Күштің нүктеге қатысты моменті деп, плюс не минус таңбамен алынған күш модулі мен осы нүктеден күштің әсер сызығына дейін түсірілген перпендикуляр ұзындығына көбейтіндісін айтады.

күші нүктесінде бекітілген денені осы нүктеге қатысты айналдыруға тырысады делік (I.1.5, а - сурет), онда күш моменті

Күштің нүктеге қатысты моментінің векторы.Қатты денеге түсірілген кеңістіктегі күштер жүйесін қарастырғандакүштің нүктеге қатысты моментінің векторы деген ұғым қолданылады.Күштің нүктеге қатысты моментінің векторы деп, осы нүктеге түсірілген және шамасы күш модулі мен осы нүктеге қарағандағы иіннің көбейтіндісіне тең векторды айтады. Күш моментінің векторы күш және моменттік нүкте жатқан жазықтыққа перпендикуляр, сонымен қатар ұшынан қарағанда күштің денені сағат тілі жүрісіне қарама-қарсы айналдыруға тырысатын бағытта түсіріледі.

Күштің О нүктесiне қатысты момент векторын , ал оның сандық мәнін деп белгілейік. Онда анықтамаға сәйкес

Күштің өске қатысты моменті. өсімен қиылыспайтын және оған параллель емес күші әсерінен өсінің төңірегінде айналу мүмкіншілігі бар денені қарастырайық (I.1.8, а – сурет). Күштің өсіне қатысты моментін табу үшін, күшін, осы өске перпендикуляр жазықтыққа ( жазықтығы) проекциялау керек. Бұл проекцияны арқылы белгілейік. Осыдан кейін осы проекцияның өсімен жазықтығының қиылысатын нүктесіне қатысты моментін табамыз

• Байланыстар мен олардың реакциялары. Механикада еркін және еркін емес денелер қарастырылады. Кеңістіктегі кез келген бағытта қозғала алатын дене еркін дене деп аталады. Егер дененің кеңістіктегі қозғалысы қандай да бір басқа денемен шектелген болса, онда ол еркін емес денедеп аталады. Берілген дененің қозғалысын шектейтін денені байланыс деп атайды. Дененің байланысқа әсер ететін күшін қысым күшідеп атайды, ал байланыстың денеге әсер күшін байланыс реакциясы немесе жай ғанареакциядейді. Өзара әсер заңы негізінде, бұл күштер бір түзудің бойымен қарама-қарсы бағыттала әсер ететін күштер. Сонымен қатар бұлар әр денеге түскендіктен күштер жиынын құра алмайды.

Денеге әсер ететін күштер актив және реактив күштер болып екіге бөлінеді. Тыныштықтағы денені қандай да бір қозғалысқа келтіре алатын күшті актив күш деп атаса, осы қозғалысқа кедергі болатын күшті реактив күш деп атайды. Актив күштердің модульдері мен бағыттары алдын ала беріледі және денеге әсер ететін басқа күштерге тәуелсіз болады, ал реактивті күштердің шамалары мен бағыттары көп жағдайда алдын ала белгісіз және денеге әсер етуші актив күштерге тәуелді болады. Актив күшті жиірек жүктеме деп атайды.

Статиканың көптеген есептерін шешкенде еркін емес денені еркін дене ретінде қарастырады. Ол мүмкіндік байланыстар аксиомасы немесе дененің босану ережесіне негізделген. Бұл аксиома былай тұжырымдалған: байланыстарды алып тастап, оларды реакциялармен алмастыру арқылы кез келген еркін емес дене актив және реактив күштер әсеріндегі еркін дене ретінде қарастыруға болады.

Реакциялардың модульдері мен бағыттары алдын ала белгісіз, модульдері актив күштердің модульдеріне тәуелді болса, бағыттары дененің қандай бағыттағы мүмкіндік қозғалысын байланыстардың шектейтініне байланысты.

Енді конструкцияларда кездесетін байланыстардың негізгі түрлеріне тоқталып, олардың реакцияларының мүмкін болатын бағыттарын көрсетейік.

1) Идеал жылтыр бет. Идеал жылтыр беттің реакциясы әр уақытта да жанасушы беттерге ортақ нормаль бойымен бағытталады (I.1.14, а - сурет).

2) Иілгіш байланыс. Мұндай байланысқа абсолют созылмайтын және салмақсыз деп құрастырылатын жіп, арқан және шынжыр жатады. Иілгіш байланыстар тек созылған жағдайда ғана жұмыс істейді, сондықтан реакциялары олардың бойымен байланыстардың ілінген нүктелеріне қарай бағытталады (I.1.14, b, c - сурет).

3) Жылжымалы топсалы тірек. Жылжымалы топса дененің тіреу жазықтығымен қозғалыс жасауына кедергі келтірмейді де, оған перпендикуляр бағыттағы қозғалысын шектейді. Сондықтан да оның реакциясы әрдайым тіреу жазықтығына перпендикуляр бағытталады (I.1.15, а, b - сурет).

4) Жылжымайтын топсалы тірек. Мұндай тірек денеге топсаны емін- еркін айнала қозғалуына мүмкіндік береді де, оның топса өсіне перпендикуляр кез келген бағыттағы ілгерлемелі қозғалысын шектейді (I.1.16, а – сурет).

Демек, жүктелген дененің топса өсіне перпендикуляр жазықтықта қандай бағытта тірекке әсер ететіні алдын-ала белгісіз. Сөйтіп, реакциясы бұл жазықтықта кез келген бағытта болуы мүмкін (I.1.16, а -сурет) Бағыты да, шамасы да белгісіз, толық реакцияның орнына әдетте оның координаталық өстердегі проекциялары анықталады. Егер 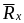және проекциялары белгілі болса, онда толық реакцияның шамасы мен бағытын 4-аксиома бойынша анықтауға болады. I.1.16, b, c - суреттерде жылжымайтын топсалы тіректің шартты кескіндеулері көрсетілген

5) Жылжымайтын сфералық топсалы тірек. Бұл топса денеге кеңістікте әсер ететін жағдайда пайдаланылады. Сфералық топса дененің бір нүктесін қозғалмайтын етіп бекітеді. Дене осы бекітілген нүктесі арқылы өтетін өспен айнала алады. Қозғалмайтын нүктедегі реакция кеңістікте кез келген бағытта болуы мүмкін. Сондықтан да ол өзінің проекциялары арқылы ізделінеді (I.1.17, а - сурет)

6) Жылжымайтын өкшелі тірек. Бұл тірек цилиндрлік топса мен жазықтық беттің байланысынан болады. Реакцияның бағыты да, шамасы да алдын-ала белгісіз, оның орны мен шамасы координаталық өстердегі жіктеулері арқылы анықталады (I.1.17, b - сурет).

7) Қатаң байланыс. Бұл тірек өзіне бекітілген дененің екі (жазық және тік) бағытта қозғалуына және дененің тірекке қарағанда бұрылуына мүмкіндік бермейді (I.1.18, а - сурет). Қатаң тіректің шартты кескіндеуі I.1.18, b, c - суретте көрсетілген. Мұндай тіректің үш реакциясы бар: тік бағыттағы жазық бағыттағы және момент . Бұл реакциялардың бағыттары мен шамалары алдын-ала белгісіз болады.

8) Қатаң стержень немесе стерженьді байланыс. Мұндай байланыс ұштарында топсасы бар, салмақсыз түзу стерженьмен жүзеге асырылады және сыртқы күш тек оның ұштарына түсетін болса, оның реакциялары тек стержень бойымен бағытталады (I.1.19 - сурет)

• Жинақталатын күштер жиыны. Жинақталатын күштер жиынының тең әсерлі күшін анықтаудың геометриялық әдісі. Әсер сызықтары бір нүктеде қиылысатын күштер жиыны жинақталатын күштер жиыны деп аталады. Берілген барлық күштердің әсер сызықтары бір жазықта жатса, онда күштер жүйесін жазық жинақталатын күштер жиыны деп, ал ол күштердің әсер сызықтары әр түрлі жазықтықта жатса, кеңістіктегі жинақталатын күштер жиыны деп атайды.

Күшті оның әсер сызығы бойымен сырғытуға болады, сондықтан әсер сызықтары қиылысатын нүктеге жинақталатын күштерді әрдайым көшіруге болады.

Теорема.Жазық жинақталатын күштер жиынының тең әсерлі күші сол күштердің векторлық қосындысына тең, оның әсер сызығы күштер жинақталатын нүктеден өтеді

Жинақталған күштердің тең әсерлі күшін анықтаудың қарастырылған әдісін геометриялық әдіс деп атайды.

Жинақталатын күштер жүйесінің тепе-теңдік шарты. Кейде күштер көпбұрышын тұрғызғанда соңғы қосылатын күштің ұшы алғашқы күштің бас нүктесіне сәйкес келуі мүмкін (I.1.22 – сурет), яғни жинақталатын күштер жиынының тең әсерлі күші нөлге тең болады.

Бұл жағдайда жинақталатын күштер жүйесітепе-теңдікте деп аталады.

Сонымен, жинақталатын күштер жиыныны тепе-теңдікте болуы үшін, күштер көпбұрышының тұйықталған болуы қажет және жеткілікті. Бұл тұжырым жинақталатын күштер тепе-теңдікте болуының геометриялық шарты деп аталады

Жазық жинақталатын күштер жынының тең әсерлі күшін, анықтаудың аналитикалық әдісі. Бір нүктеге түсірілген екі күштің тең әсерлі күшінің модулі мен бағытын аналитикалық тәсілмен де анықтауға болады, ол үшін, үшбұрышын қарастырайық (I.1.23 - сурет). , .

Косинустар теоремасы бойынша,

,

бұдан тең әсерлі күші модулі,

(I.1.13)

Синустар теоремасы бойынша,

. (I.1.14)

Осы тепе-теңдіктен тең әсерлі күштің әсер ету бағытын анықтаймыз

.

Жазық жинақталатын күштер жиынының тепе-теңдігінің аналитикалық шарты. Егер берілген жазық жинақталатын күштер жиыны тепе-теңдікте болса, онда жүйенің тең әсерлі күші нөлге тең, яғни .

Ал тең әсерлі күш нөлге тең болса, демек оның проекциялары да нөлге тең болады,

• Жазық қос күштер жүйесі. Қос күш және қос күш моменті. Жоғарыда біз күштердің шамасы әр түрлі болған жағдайдағы қарама-қарсы бағытталған екі параллель күшті қосуды қарастырғанбыз. Енді қарама-қарсы бағытталған параллель екі күштің шамалары өзара тең болған жағдайын қарастырайық (I.1.25, а – сурет). , , ,

Модульдері тең және қарама-қарсы бағытталған екі параллель күш жүйесін қос күш деп атайды.

ғасырдың басында француз ғалымы Пуансо (1777-1859) механикаға қос күш ұғымын енгізіп, қос күштер теориясын тұрғызады. Қос ұғымымен қатар қос күш механикада негізгі ұғымдардың бірі болып табылады.

Қос күш құрайтын күштер орналасқан жазықтық қос күш әсерінің жазықтығы, ал күштердің ара қашықтығы қос күш иіні деп аталады. Қос күштің денеге әсері денені айналысқа келтіруге тырысатынымен сипатталады. Қос күштің денеге жасайтын мұндай әсері күштің шамасы мен иініне, әсер жазықтығының орналасуына және осы жазықтықтағы қос күштің айналу бағытына тәуелді болады. Қос күш әсері қос күш моментімен анықталады.

Қос күш моменті деп плюс не минус таңбамен алынған қос күш құраушы күштердің бірінің модулі мен оның иінінің көбейтіндісін айтады (I.1.25, b – сурет)

Қос күш моментінің негізгі қасиеттері.Бірінші қасиеті. Қос күштің тең әсерлі күші болмайды.

Иіні болатын, қос күш берілсін делік және болсын (I.1.27, а - сурет).

Олай болса, бұл күштер жүйесінің тең әсерлі күші

тең болады, ал оның түсу нүктесі келесі пропорциядан анықталады

Сонымен, қос күшті бір күшпен теңгеру мүмкін еместігін және қос күшті тек қос күшпен теңгеруге болатынын тұжырымдаймыз.

Екінші қасиеті. Қос күштің құраушы күштерінің әсер жазықтығындағы кез келген нүктеге қатысты алынған моменттірінің алгебралық қосындысы қос күш моментіне тең.

Иіні болатын қос күш беріліп оның күш моменті

Қос күштің бұл қасиетінен мынаны тұжырымдауға болады: кез келген момент центрлеріне қатысты құрылған момент теңдеулеріне қос күш бірдей таңбамен және бірдей шамамен кіреді, яғни қос күш моментінің таңбасы мен шамасы момент центрінен тәуелсіз.

Үшінші қасиеті. Қос күштің құраушы күштерінің өске проекцияларының алгебралық қосындысы әрқашан нөлге тең.

қос күші және қос күштің әсер жазықтығында жататын өсі берілсін делік (I.1.28 - сурет).

Суретте көрсетілген және үшбұрыштарының теңдігінен екені аңғарылады.

• Қос күштер эквиваленттілігі. Еркін қатты дененің механикалық күйін өзгертпей бір қос күшті екінші бір қос күшпен алмастыруға мүмкін болса, онда бұл қос күштер пара-пар немесе эквивалентті деп аталады.

1 теорема.Қос күштің денеге әсер, оны әсер ету жазықтығында басқа орынға ауыстырғаннан өзгермейді.

Иіні қос күші беріліп, қос күшті иіні болатын кездейсоқ алынған орынға ауыстыру қажет болсын делік (I.1.29, а – сурет).

мен және мен нүктелерінен, сәйкесінше және кесінділеріне перпендикуляр, параллель түзулер жүргізейік (I.1.29, b – сурет). Екі параллель түзудің екінші параллель түзумен қиылысады және қиылысында 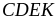ромб пайда болады (өйткені берілгені бойынша , ал параллелограмның бір төбесінен түсірілген биіктіктер тең болса, онда ол ромб). күшін әсер ету сызығының бойымен нүктесінен 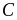нүктесіне, ал 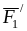күшін нүктесінен нүктесіне түсірейік. түзуінің бойымен нүктесіне, модульдері -ге тең теңестірілген және күштер жиынын түсірейік; түзуінің бойымен нүктесіне де модульдері -ке тең, теңестірілген және күштер жүйесін түсірейік, сонымен .

2 теорема. Бір жазықтықта жатқан, моменттері тең екі қос күштің денеге әсерлері өзгермейді.

Бір жазықтықта жататын, әсер ететін моменттері тең қос күштер статикалық тепе-тең деп аталады

• Жинақталатын күштер жиыны. Жинақталатын күштер жиынының тең әсерлі күшін анықтаудың геометриялық әдісі. Әсер сызықтары бір нүктеде қиылысатын күштер жиыны жинақталатын күштер жиыны деп аталады. Берілген барлық күштердің әсер сызықтары бір жазықта жатса, онда күштер жүйесін жазық жинақталатын күштер жиыны деп, ал ол күштердің әсер сызықтары әр түрлі жазықтықта жатса, кеңістіктегі жинақталатын күштер жиыны деп атайды.

Күшті оның әсер сызығы бойымен сырғытуға болады, сондықтан әсер сызықтары қиылысатын нүктеге жинақталатын күштерді әрдайым көшіруге болады.

Теорема.Жазық жинақталатын күштер жиынының тең әсерлі күші сол күштердің векторлық қосындысына тең, оның әсер сызығы күштер жинақталатын нүктеден өтеді

Жинақталған күштердің тең әсерлі күшін анықтаудың қарастырылған әдісін геометриялық әдіс деп атайды

Тұрғызылған көпбұрышты (I.1.21, b – сурет) күштер көпбұрышы деп атайды. Осы көпбұрыштың тұйықтаушы қабырғасы берілген күштер жүйесінің тең әсерлі күшін, кескіндейді. Тең әсерлі күш бағыты әрдайым сәйкесінше біртіндеп берілген күштерді қосумен тұрғызылған көпбұрыштың орғыту бағытына қарама-қарсы болады.

Қос күштерді қосу.

Қос күштердің тепе-теңдік шарты. Теорема.

Денеге бір жазықтықта әсер ететін қос күштер жиыны, моменті қос күштердің моменттерінің алгебралық қосындысына тең болатын қос күшпен тепе-тең.

Сонымен, денеге бір жазықта әсер ететін бірнеше қос күштерді қосу үшін, осы қос күштерінің моменттерінің алгебралық қосындысын анықтаса жеткілікті. Қосу нәтижесінде алынған момент тең әсерлі қос күшті анықтайды.

яғни денеге бір жазықта әсер етуші қос күштер жиыныі тепе-теңдікте болу үшін жиындағыі қос күштер моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

Еркінжазықкүштержүйесі. Жазықпараллелькүштержүйесі. Күштіберілгеннүктегекелтіру.

денеге әсер ететін кез келген күшті дененің қандай да бір нүктесіне өзіне-өзі параллель көшіруге болады, бұл жағдайда келтіру нүктесіне күшпен қатар моменті берілген күштің жаңа түсіру нүктесіне қатысты моментіне тең қос күшті қосу қажет.

Осы сияқты күштің орнын ауыстыруды күшті берілген нүктеге келтіру деп атайды

Әсер сызықтары бір жазықта жататын және параллель болатын күштер жиынын жазық параллель күштер жиыны деп айтады. Физика курсынан белгілідей (I.1.24, а - сурет) бір бағытталған екі параллель күштің тең әсерлі күші берілген күштер қосындысына тең де, осы күштерге параллель және бағыттас болады, ал оның әсер сызығы берілген екі күштің түсу нүктелерін қосатын кесіндіні сол күштердің модульдеріне кері пропорционал болатындай етіп екі бөлікке іштей бөлетін нүктеден өтеді, яғни

, , , , .

Еркін жазық күштер жүйесін берілген нүктеге келтіру.

денеге әсер ететін кез келген күшті дененің қандай да бір нүктесіне өзіне-өзі параллель көшіруге болады, бұл жағдайда келтіру нүктесіне күшпен қатар моменті берілген күштің жаңа түсіру нүктесіне қатысты моментіне тең қос күшті қосу қажет.

Осы сияқты күштің орнын ауыстыруды күшті берілген нүктеге келтіру деп атайды,

Жазықкүштержүйесініңтеңәсерлікүші. Вариньонтеоремасы.

Сәйкес күштердің тең әсерлі күші мен моментінің арасындағы тәуелділік жөніндегі теореманы француз ғалымы Вариньонның есімімен – Вариньон теоремасы деп аталады.

Теорема.Кез келген жазық күштер жиынының қандай да бір келтіру нүктесіне қатысты алынған тең әсерлі күшінің моменті осы нүктеге қатысты алынған жиынның құрама күштер моменттерінің алгебралық қосындысына тең.

Шын мәнінде I.1.35 – суретте көрсетілгендей, тең әсерлі күштің нүктесіне қарағандағы моменті , мұндағы , олай болса,

Демек,

.

(I.1.31) формуласына сәйкес

,

сондықтан

. (I.1.35)

Теорема дәлелденді.

Еркінбағытталғанжазықкүштержүйесініңтепе-теңдікшарты. Кеңістіктегікүштержүйесі.

Еркін бағытталған жазық күштер жиынының тепе-теңдік шарты. Егер еркін бағытталған күштердің бас векторы нөлге тең болса, онда оның модулі де нөлге тең, яғни болса, онда немесе , .

Осы теңдіктерден тепе-теңдіктің келесі шарттарын аламыз:

1 Еркін бағытталған жазық күштер жиынының тепе-теңдікте болуы үшін жиынды құраушы күштерінің екі координат өстеріндегі проекцияларының алгебралық қосындысы және күш жазықтығындағы кез келген бір нүктеге қатысты алынған күштер моменттерінің алгебралық қосындысы нөлге тең болулары қажет және жеткілікті

, , . (I.1.37)

Бұл өрнектерді тепе-теңдіктің шарты немесе тепе-теңдік теңдеуі деп атайды.

2 Еркін бағытталған жазық күштер жиынының тепе-теңдікте болуы үшін кез келген екі және нүктелеріне қатысты жиынды құраушы күштер моменттерінің алгебралық қосындысы мен түзуіне перпендикуляр болып келмеген қандай да бір өстегі (мысалы, өсін алайық) осы күштер проекцияларының алгебралық қосындысы нөлге тең болулары қажет және жеткілікті

, , . (I.1.38)

3 Еркін бағытталған жазық күштер жүйесінің тепе-теңдікте болуы үшін жүйенің құрама күштерінің бір түзудің бойында жатпайтын кез келген , және нүктелеріне қатысты моменттерінің алгебралық қосындысы нөлге тең болулары қажет және жеткілікті

, ,

Арқалықты жүйелер. Жүктемелердің түрлері

Аркалық деп кандай да бір құрылымның тузу білік түрінде екі немесе оданда көп нүктесінде тірегі бар конструкциялық тетігін айтамыз.

Ауырлық центрі.

Дене бөлшектерінің ауырлық күштерінен құралған паралель күштер жүйесінің центрін дененің ауырлық центрі деп атайды.

Жазық қималардың геометриялық сипаттамалары. Жазық қималардың статикалық моменттері, еркін моменттері және кедергі моменттері.

Интегралдармен анықталатын геометриялық сипаттамаларды қиманың статикалық моменттері дейміз.

Берілген қиманың кез келген өзара перпендикуляр өстеріне қарағандағы центрден тепкіш екпін моменті деп, төмендегі интегралмен анықталатын геометриялық сипаттаманы айтамыз:

Параллель осьтерге қатысты екпін моменттерінің байланысы (өзгеруі).

Бұл тәуелділікті анықтау үшін, ауданы қиманы (I.2.25 - сурет) қарастырайық. Қиманың ауырлық центрінен өзара перпендикуляр өстері жүргізілген. Ауырлық центрден өтетін өстерді центрлік өстер деп, ал центрлік өстерге қарағандағы екпін моменттерін центрлік екпін моменттерідеп атаймыз.

Қиманың центрлік екпін моменттері берілген деп қарастырып, центрлік өстерге параллель өстеріне қарағандағы екпін моменттерінің шамаларын анықтайық.

Бөлініп алынған шексіз кіші ауданының жүйесіндегі координаттары , ал жүйесіндегі координаттары болсын. Онда, анықтама бойынша, қиманың өсіне қарағандағы екпін моменті

Анықтама бойынша, мұндағы

; ;

және центрлік өске қарағандағы қиманың статикалық моменті нөлге тең, олай болса

Дәл осылай және анықталады, сонымен

;

; (I.2.54)

,

яғни, қиманың кез келген центрлік өсіне параллель өске қарағандағы өстік екпін моменті, центрлік екпін моментіне қиманың ауданын осы өстердің ара қашықтығының квадратына көбейтіп қосқанға тең, ал центрден тепкіш екпін моменті, центрлік өстерге қарағандағы центрден тепкіш екпін моментіне қиманың ауданын осы өстердің ара қашықтықтарына көбейтіп қосқанға тең.

Бұралған осьтерге қатысты екпін моменттерінің байланысы (бұралуы).

Суретте көрсетілген (I.2.26 - сурет) қиманың және өстеріне қарағандағы және екпін моменттері берілген болсын делік. Енді өс жүйесін қандай да бір бұрышына бұрайық және, әмендегідей, сағат тіліне қарсы бұрылған бұрышты оң таңбалы деп ұйғарамыз. деп қабылдайық. Жаңа және өстеріне қарағандағы екпін моменттерін анықтайық.

Ол үшін, шексіз кіші ауданының пен жүйелеріндегі координаттарының арасындағы өзара байланысын анықтайық ( )

Олай болса,

жалпы (I.2.35) заңдылыққа байланысты

.

Центрден тепкіш екпін моментін (1.38) өрнегінен табамыз

Сонымен,

(I.2.55)

(I.2.56)

(I.2.57)

Алынған (I.2.55) және (I.2.56) өрнектерін қоссақ

екенін көреміз, яғни өзара перпендикуляр өстерге қарағандағы екпін моменттерінің қосындысы осы өстерді кез келген бұрышқа бұрғаннан өзгермейді.

1. Екпіннің бас осьтері мен бас моменттері.

2. Созылу мен сығылу.

3. Деформация мен орын ауыстыру.

4. Материалдар кедергісінің негізгі ұғымдары.

5. Конструкция және оның есептеу моделі.

6. Сыртқы күштер және олардың сұрыптамасы, түрлері.

7. Ішкі күштер . Қию әдісі

8. Ығысу . Ығысу кезіндегі беріктік шарты.

9. Созылу мен сығылу кезіндегі беріктік шарты. Салыстырмалы деформация.

10. Толық, тік, жанама кернеулер. Орын ауыстыру және деформациялар.

• Екпіннің бас өстері мен бас моменттері Жоғарғы өрнектер бұрылған өстерге қарағандағы екпін моменттерінің шамалары бұрылу бұрышына тәуелділігін көрсетеді, яғни бұрылу бұрышының қандай да бір мәнінде бұрылған өстерге қарағандағы екпін моменттері экстремальді мәндеріне жетуі мүмкін. Осы бұрыштың мәнін анықтап көрейік. Ол үшін (I.2.55) немесе (I.2.56) өрнегінен бір рет туынды алып, оны нөлге теңестірейік

немесе

бұдан . Бұл формула бойынша бұрыштың екі мәні бар бірі - , екіншісі - .

Осыдан мынадай тұжырымдама жасауға болады: екпін моменттері экстремальді мәндеріне орны (I.2.59) өрнегімен анықталатын, өзара перпендикуляр, екі өске қарағанда ие болады. Бұл өстерді бас екпін өстері деп, ал осы өстерге қарағандағы өстік екпін моменттерін бас екпін моменттері деп атайды. Бас екпін өстеріне қарағандағы центрден тепкіш екпін моменті нөлге тең. Бас екпін өстерін деп белгілеу қабылданған.

Егер (I.2.59) формуласынан анықталған бұрыш болса, бас екпін өстері алғашқы өстеріне қарағанда сағат тілінің жүрісіне қарама-қарсы бағытта бұрылады, ал болса, сағат тілінің жүрісі бағытымен бұрылады.

Енді бас екпін моменттері мәндерінің анықталу жолын қарастырайық. Ол үшін, (I/2.55) және (I.2.56) өрнектеріндегі - ның орнына -ді қойып, бас екпін моменттерін анықтайтын өрнектер аламыз

Белгілі тригонометриялық функцияларды пайдалана отырып, бас екпін моменттерін анықтайтын (I.2.60) формулаларын келесі түрге келтіруге болады

.

Егер болса, максимум өсі өсіне, ал болса, максимум өсі өсіне жақын орналасады, яғни егер болса, , ал болса, .

Өстік екпін моменті мен қима ауданының арасындағы тәуелділікті көрсететін шама

қиманың екпін радиусы деп аталады, өлшем бірлігі - ендік бірлік

• ДЕФОРМАЦИЯ МЕН ОРЫН АУЫСТЫРУ

Қандай дене болмасын сыртқы күш әсерінен өздерінің өлшемдері мен формаларын өзгертеді, деформацияланады.

Дененің сызықты өлшемдерінің өзгеруі сызықтық деформация, ал бұрыштық өлшемдерінің өзгеруі бұрыштық деформация делінеді.

Деформация нәтижесінде дененің сызықтық өлшемінің өcyi – созылу (ұзару), ал кемуі – сығылу (қысқару) деп аталады.

Деформация материалдың атомдарының ара қашықтықтарының өзгеруі мен атом блоктарының орын ауыстыруы салдарынан туады. Оның табиғатын толық зерттеп білу үшін, жазық дененің кез келген нүктесінің жанынан өзара перпендикуляр АВ, СA түзулерін алайық (I. 3, а-сурет).

Дене деформацияланғанда АС түзу сызығы шамасына ұзарады (I. 3, б-сурет). Оның орташа сызықтық салыстырмалы деформациясы келесі формуламен анықталады.

(1.01)

1.3-сурет

Бұл қатынастың бөліміндегі АС кесіндісінің ұзындығы нөлге ұмтылғандағы шегі, А нүктесіндегі толық салыстырмалы деформацияны аныктайды

. (1.02)

Енді бұрыштық деформацияны қарастырайық. Деформацияға дейінгі ВАС тікбұрышы мен деформациядан кейінгі В'А'С сүйір бұрышының арасындағы айырма берілген нүктенің бұрыштық деформациясын сипаттайды.

Сонымен күш түскен дененің кез келген нүктедегі деформациясы сызықтық салыстырмалы және бұрыштық деформациялармен сипатталады. Денеде пайда болған сызықтық және бұрыштық деформациялар сырттан әсер етуші күш жойылғанда толық жойылуы немесе жойылмауы да мұмкін. Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деп, ал деформация толық жойылмай қалса, онда қалдық деформацияны пластикалық деформация деп атайды. Егер дененің бекіту шарттары мен нүктелеріндегі деформацияның шамасы белгілі болса, онда кез келген нүктенің деформациядан кейінгі орнын, яғни орын ауыстыру шамасын анықтауға болады. Машина бөлшектері серпімді деформацияланғанда ғана, олардың жұмыс істеу қабілеті қамтамасыз етіледі. Сондықтан, нүктелердің ең үлкен орын ауыстыру шамасы белгілі бip мүмкіндік шамадан аспауы керек. Мұндай шарт теңсіздік ретінде көрсетіліп, қатаңдық шарты деп аталады.

7 – сұрақ

Ішкі күштер дененің бір бөлігімен екінші бөлігіне көлденең қима арқылы үздіксіз жайыла таралып беріледі Олардың әсер ету заңдылығын білу үшін қима бетінде жатқан нүктесін қарастырайық (1.5, а-сурет). Нүктені қоршаған шексіз кіші ауданды , ал ол ауданға сәйкес келетін ішкі күшті деп белгілейік. Ішкі күш ның шексіз кіші аудан ке қатынасы

1.5-сурет

нүктесіндегі ішкі күштің орташа шамасын – орташа кернеуді аңықтайды.

. (1.04)

Шексіз кіші аудан нөлге ұмтылғандағы көрсетілген қатынастың шегі В нүктесіндегі толық кернеу деп аталады:

. (1.05)

Толық кернеудің көлденең қима жазықтығына перпендикуляр OZ өсте, түсіріген проекциясы тік кернеу деп аталып, OZәрпімен белгіленеді, ал қима бетіне түcipiлгeн проекциясы жанама кернеу деп

1.6-сурет

аталып, әрпімен белгіленеді (1.5, б-сурет).

Суреттен, толық кернеу 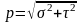,екендігін көреміз.

• Созылу мен сығылу.

Созылған (сығылған) білеуді беріктікке есептеу. Машиналар мен құрылымдарды және олардың элементтерін жобалағанда, негізінен келесідей үш есептің түрлерімен кездесуге болады: 1) Жобалау есебі, яғни берілген күштердің шамасына сәйкес, таңдап алынған материалдан жасалынатын конструкция элементінің беріктігін, қатаңдығы мен жеткілікті тӛзімділігін қамтамасыз ететін қиманың ең аз ӛлшемдерін анықтау. 2) Беріктікті тексеру есебі, яғни белгілі күштердің шамасы мен конструкция элементтерінің кӛлденең қима ӛдшемдері бойынша элементтердегі нақтылы кернеулердің ең үлкен шамасын анықтап, мүмкіндік кернеумен салыстыру. 3) Жүк кӛтеру қабілетін анықтау есебі, яғни белгілі конструкция элементтерінің кӛлденең қима ӛлшемдері мен материалдарының мүмкіндік кернеуі бойынша конструкция элементтерінің жүк кӛтеру қабілетін анықтау. Созылу мен сығылу деформацияның беріктік шарты келесі формуламен өрнектеледі.

Созылудеформациясыменшынжырларды, арқандарды, болттарды, әр

түрліаспалардыесептеудекездессек, сығылудеформациясыіргетастармен

тіректердіесептеудеқарастырылады.

Білеугеәсеретушікүштердісозушыкүштердепқарастырсақ, (I.2.8, b -

сурет) ондабілеудіңұзындығы

(I.2.6)

шамасынаұзарады (созылады), алені

b b₁b₀(I.2.7)

шамасынақысқарады (сығылады).

Білеудіңбастапқыұзындығыныңұзарушамасын- абсолютұзару, ал

енініңқысқарушамасынb - абсолютқысқарудепатаймыз.

немесеb шамаларыбойыншабілеудіңдеформациялануқабілетін

сипаттауғаболмайды, ӛйткеніабсолютұзаруменқысқарубілеугеәсеретушікүшпенқатарбілеудіңбастапқыӛлшембірліктерінебайланысты. Сондықтансозылғаннемесесығылғанбілеудіңдеформацияланушамасынсипаттауүшін, абсолютұзарудыңбілеудіңалғашқыұзындығына, алабсолютқысқарудыңбілеудіңалғашқыенінеқатынастарыналғандұрыс, яғни

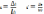
мұндағы E- бойлықсалыстырмалыдеформациясыдеп, ал E’- ендіксалыстырмалыдеформациядепаталады. формулаларынан E мен E’ ӛлшембірліксізшамаларекенінкӛреміз

• Материалдар кедергісінің негізгі ұғымдары.

«Материалдар кедергісі» деп машина мен конструкциялардың бөліктерінің беріктігі, қатаңдығы және орнықтылығы туралы ғылымды айтамыз.

Беріктік деп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсеріне қирамай қарсыласу қабілетін айтады.

Қатаңдық деп конструкция мен оның элементтерінің деформацияға қарсыласу қабілетін атайды.

Орнықтылық деп конструкцияның немесе оның элементтерінің белгілі алғашқы серпімді тепе-теңдік күйін сақтау қабілетін айтады. Есептеу денелерінің түрлері. Инженерлік практикада кездесетін сан алуан конструкция элементтері пішіндері мен ӛлшемдеріне байланысты жинақталып, тӛмендегідей қарапайым түрлерге жіктелген: 1 Білеу (брус) - екі ӛлшемі үшін,шісінен әлдеқайда кіші дене (I.2.1, а, b - сурет). Дербес жағдайда білеудің кӛлденең қимасының ауданы тұрақты, ал ӛсі түзу сызықты болуы мүмкін (I.2,1, b - сурет).

Ӛсі түзу сызықты білеуді стержень деп атайды. Білеудің өсі дегеніміз кӛлденең қималардың ауырлық центрлерінің геометриялық орны (I.2.1, c - сурет). 2 Пластина – ара қашықтығы басқа ӛлшемдеріне қарағанда ӛте кіші, екі жазық бетпен шектелген дене (I.2.2, а - сурет). 3 Қабықша - ара қашықтығы басқа ӛлшемдеріне қарағанда әлдеқайда кіші болатын екі қисық сызықты беттермен шектелген дене (I.2.2, b - сурет).

4 Массив - үш ӛлшемдері ӛзара шамалас дене (I.2.2, с - сурет). «Материалдар кедергісі» пәнінде қатаңдығы жеткілікті, аз деформацияланатын, кӛбінесе кӛлденең қималары тұрақты, білеу тәріздес жұмыр денелер немесе олардан құрылған қарапайым жүйелер қарастырылады.

• Конструкция және оның есептеу моделі.

• Сыртқы күштер және олардың сұрыптамасы, түрлері.

Сыртқы күштер. Материалдар кедергісі есептерін шешкенде, ең алдымен конструкция элементтеріне әсер ететін сыртқы күштің шамасы мен түсу сипатын анықтап алу қажет. Белгілідей, сыртқы күш деп денелердің бір- бірімен әсерін, демек, сол конструкция элементтерінің өзара әсерін де айтады. Сол сияқты берілген конструкция элементінің басқа денемен әсері қарастырылған элемент үшін, сыртқы күш болып табылады. Мысалы, шамға құйылған жермайдың салмағы шан орнатылған тұғырға түседі, одан тұғырдың аяқтары арқылы іргетасқа түседі. Элементтің өз салмағы да сыртқы күшке жатады.

Сыртқы күштер көлемдік және беттік болып бөлінеді. Беті арқылы берілетін сыртқы күшбеттік, ал көлемі арқылы берілетін сыртқы күш көлемдік күш деп аталады.

Беттік күштер қадалғаннемесе таралған күш болуы мүмкін.

Қадалған күш деп, конструкция элементтеріне өз өлшемдерімен салыстырғанда өте шағын аудан арқылы берілетін күшті айтады. Қадалған күштің өлшем бірлігі ньютон (Н), килоньютон (кН), меганьютон (МН). Мысалы, тісті берілістегі тістердің бір-біріне әсері. Ауданның өте шағындығына байланысты қадалған күш әдетте денеге нүкте арқылы беріледі деп есептелінеді.

Таралған күш деп не элементтің барлық көлеміне (көлемдік күш), не белгілі бір ауданына (жазықтық күш), не белгілі бір ұзындыққа (сызықтық немесе бойлық жүк) үздіксіз түсірілген күшті айтады. Ол қарқындылығымен сипатталады. Қарқындылық деп күштің бірлік көлемге немесе бірлік ауданға немесе бірлік ұзындыққа түсірілген шамасын айтады. Қарқындылық латынша q әрпімен белгіленеді, сәйкесінше таралған күштердің өлшем бірлігі: көлемдік күш - ; жазықтық күш - ; , ;сызықтық немесе бойлық күш - ; , .

Бұл күштер таралу заңдылықтарына байланысты біркелкі таралған тұрақты және бірқалыпсыз таралған айнымалы күштер деп жіктеледі. Біркелкі таралған тұрақты күштің кез келген нүктедегі қарқындылығы өзара тең, ал бірқалыпсыз таралған айнымалы күштің қарқындылығы әр түрлі.

Денеге тұтас көлемі арқылы берілетін күштер қатаң түрде үздіксіз біркелкі тараған деп қарастырылады.

Көлемдік күшке мысал ретінде дененің салмағын, жазықтық күшке – будың қазан қабырғасына қысымын, сызықтық күшке – ені ұзындығынан өте аз арқалыққа ұзына бойлы түсірілген күшті келтіруге болады.

Сыртқы күш әсер ететін уақытына байланысты да екі топқа бөлінеді: тұрақты күшжәне уақытша күш.

Тұрақты күш деп мөлшері мен бағыты өзгермейтін күшті айтады. Егер денеге түскен күштердің шамасы немесе бағыты уақытқа байланысты өзгеріп отырса, ондай күштерді айнымалы күштер деп атайды.

Сыртқы күштерді статикалық және динамикалықкүштер деп те топтастыруға болады.

Статикалық күш деп өзінің шамасын немесе түсу нүктесін баяу жылдамдықпен өзгертетін, осы жағдайда туындауы мүмкін үдеуді ескермеуге болатын күшті атайды. Мұндай күш әсерінен конструкцияның және оның элементтерінің тербелісі мардымсыз аз болады.

Динамикалық күш деп уақытқа байланысты үлкен жылдамдықпен өзгеретін күшті айтады. Мұндай күштің әсерінен конструкция немесе оның элементтері елеулі тербелістерге ұшырайды. Тербеліс жылдамдығының өзгеруіне байланысты конструкцияда пайда болатын, оның массасы мен үдеуінің көбейтіндісіне тура пропорционал екпін күші шамасы жағынан конструкцияда тербеліс тудырушы сыртқы күштің шамасынан бірнеше есе үлкен болуы мүмкін.

Динамикалық күштер соққы, айнымалы–қайталанбалы және т. б. түрлерге жіктеледі.

Соққы күш деп кинетикалық энергиясы бар қозғалыстағы дененің екінші бір денеге соқтығысуы арқылы берілетін күшті айтады.

Айнымалы–қайталанбалыкүштер деп машина бөлшектеріне уақытқа тәуелді, периодты түрде қайталанып түсетін күштерді атайды. Мысалы, қозғалыстағы машинаның шатун, білік сияқты бөліктеріне немесе темір жол вагонының өсіне түсетін күштер айнымалы – қайталанбалы күштерге жатады.

Жалпы жағдайда күш уақытқа тәуелді күрделі заңдылықпен өзгеруі мүмкін.

• Ішкі күштер . Қию әдісі

Ішкі күштер дененің бір бөлігімен екінші бөлігіне көлденең қима арқылы үздіксіз жайыла таралып беріледі Олардың әсер ету заңдылығын білу үшін қима бетінде жатқан нүктесін қарастырайық (1.5, а-сурет). Нүктені қоршаған шексіз кіші ауданды , ал ол ауданға сәйкес келетін ішкі күшті деп белгілейік. Ішкі күш ның шексіз кіші аудан ке қатынасы

1.5-сурет

нүктесіндегі ішкі күштің орташа шамасын – орташа кернеуді аңықтайды.

. (1.04)

Шексіз кіші аудан нөлге ұмтылғандағы көрсетілген қатынастың шегі В нүктесіндегі толық кернеу деп аталады:

. (1.05)

Толық кернеудің көлденең қима жазықтығына перпендикуляр OZ өсте, түсіріген проекциясы тік кернеу деп аталып, OZәрпімен белгіленеді, ал қима бетіне түcipiлгeн проекциясы жанама кернеу деп

1.6-сурет

аталып, әрпімен белгіленеді (1.5, б-сурет).

Суреттен, толық кернеу ,екендігін көреміз.

• Ығысу . Ығысу кезіндегі беріктік шарты.

ЫҒЫСУ

Денеден бөлініп алынған шексіз кіші элементтің аудандарында тек жанама кернеулер әсер етсе, мұндай кернеулі күй таза ығысу, ал аудандары таза ығысу аудандары деп аталады (3.2-сурет). Таза ығысу – жазық кернеулі күйдің жеке біp түpi. Жалпы жағдайда, жазық кернеулі күйдің басты кернеулері келесі формуламен анықталады

.

Таза ығысу үшін болғандықтан

Немесе , .

Басты аудандарының орнын анықтау үшін бұрышын анықтаймыз

Демек, басты аудандар мен таза ығысу аудандарының арасындағы бұрыш

Енді біp шеті қатаң, бекітілген тік төртбұрышты элементтің таза ығысыпдеформациялануын зерттейік (3.2-сурет). Жанама кернеудің әсерінен А нүктесінің орын ауыстыру шамасы элементтің абсолют ығысуын, ал бұрышы салыстырмалы ығысуын анықтайды.

үшбұрышынан .

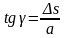Деформация серпімді болғандықтан бұрышының шамасы өте аз, сондықтан

(3.02)

Ең үлкен бас кернеудің бағытында жатқан DB диагоналінің абсолют созылуы

,

салыстырмалы созылуы .

DBC үшбұрышынан екенін ескерсек,

. (3.03)

Таза ығысу үшін болғандықтан, элементтің DB диагоналі бойындағы деформация

. (3.04)

Енді, 3.03, 3.04 теңдіктерін салыстырсақ , осыдан, ығысу деформациясы үшін Гук заңын аламыз

. (3.05)

Мұндағы – жанама кернеу мен ығысу бұрышының арасындағы пропорционалдық коэффициент (екінші текті серпімділік модулі).

Алынған 3.01, 3.02, 3.05 формулаларын пайдаланып, абсолют ығысу үшін Гук заңын алуға болады

. (3.06)

Таза ығысу деформациясының потенциялық энергиясы

ал меншікті потенциялық энергиясы

.

Таралған күштің қарқындылығы, жанама күш, ию моменті араларындығы дифференциалдық байланыс

Бip қалыпты таралған күштің қарқындылығы, жанама күш, ию моменті аралағындағы дифференциалдық байланыстарды анықтау үшін 6.4-суреттегі арқалықты қарастырайық. Сол жақтағы А тірегінен z қашықтығында жатқан көлденең қимада пайда болатын жанама күштің өрнегі

, (6.02)

ал қашықтығында жатқан көлденең қимадағы жанама күштің өрнегі

(6.03)

Соңғы 6.03 теңдеуінен 6.02 теңдеуін алып

немесе (6.04)

екенін көреміз.

Демек, кез келген қимадағы жанама күштің өрнегінен z бойынша алынған бірінші туынды, сол аралықтағы әсер етуші бip қалыпты таралған күштің қарқындылығына тең.

Абсциссасы -ке тең көлденең қимадағы ию моменті

(6.05)

ал абсциссасы z+dz-ке тең көлденең қимадағы ию моментінің өрнегі

5.5-сурет

(6.06)

Соңғы (6.06) теңдігінен (6.05) теңдігін алып

(6.07)

екенін көреміз.

Демек, кез келген көлденең қимадағы ию моментінің өрнегінен z бойынша алынған бірінші туынды, осы қимадағы жанама күшке тең. Олай болса

(6.08)

Көлденең қимадағы ию моментінің өрнегінен z бойынша алынған екінші туынды осы аралықта әсер етуші бip қалыпты , таралған күштің қарқындылығына тең.

Алынған 6.04, 6.07, 6.08 теңдіктер жанама күш, ию моменті, таралған күштің қарқындылығы аралағындағы дифференциалдық байланыстар деп аталады.

. Жанама күш пен ию momehtі

Қос терікті иілген арқалықтың көлденең қималарындағы ішкі күштерді анықтайық . Кез келген т-т қимасындағы ішкі күштерді табу үшін, қию әдесі бойынша, сол қима арқылы арқалықты екіге бөліп, біp бөлігін алып тастаймыз. Алып тасталынған бөліктің қалған бөлікке әсерін көлденең күш пен ию моментімен алмастырамыз. Қалған бөлік сыртқы күштер мен ішкі күштердің әсерінен тепе-теңдік күйде болуы тиіс.

Статиканың бірінші теңдеуі

осыдан

яғни кез келген т-т қимасындағы көлденең күш Q(z), сол қиманың біp жағында әсер етуші сыртқы күштердің У өсіне түсірілген проекцияларының алгебралық қосындысына тең. Статиканың екінші тендеуі

осыдан

Яғни, кез келген т-т қимасындағы ию моменті М( ) сол қиманың біp жағында жатқан сыртқы күштердің С нүктесіне қарағандағы моменттерінің алгебралық қосындысына тең (С нүктесі т-т қимасының ауырлық центрі).

6.2-сурет

Бір қалыпты таралған күштерді өсіне проекциялау үшін немесе С нүктесіне қарағандағы моментін анықтау үшін оларды биіктігі q-ға, ұзындығы -ке тең тік төртбұрыштың ауырлық центрі арқылы өтетін қорытынды R_q = Qzкүшімен алмастырады.

Көлденең күш пен ию моментінің таңбалары туралы келесі ережелер қабылданады. Көлденең т-т қимасының сол жағында әсер eтiп тұрған сыртқы күштердің қорытынды күші (R) төменнен жоғары қарай ал оң жақтағы сыртқы күштердің қорытынды күші (R) жоғарыдан төмен қарай бағытталған болса, ол қимадағы жанама күш Q(z) оң таңбалы болып саналады. Кері жағдайда жанама теріс таңбалы. Көлденең қимасының сол жағындағы әсер етуші сыртқы күштердің осы қиманың ауырлық центріне қарағандағы қорытынды моменті (М) сағат тілімен бағыттас, ал оң жағындағы күштердің қорытынды моменті сағат тіліне қарсы бағытта болса, ол қимадағы ию моменті оң таңбалы деп саналады (6. 3, а-сурет). Kepi жағдайда ию моменті M(z) теріс таңбалы (6. 3, б-сурет).