Генераторы случайных чисел(общие сведения)
Служат для генерации случайных чисел( СЧ важны для моделирования стохастических воздействий)
Есть 3 способа генерации:
1. Аппаратный (физический)
Генерация случайных чисел осуществляется специальным электронным устройством, называемым датчиком случайных чисел (генераторы белого шума).
Достоинства:
- отсутствие дополнительных вычислительных операций по ЭВМ
- неограниченный запас случайных чисел
- не требуется дополнительная память
- высокая скорость
- генерация «хороших» случайных чисел.
Недостатки:
- отсутствие гарантии качества случайных чисел непосредственно во время моделирования
- невозможность повторения при моделировании той самой последовательности случайных чисел
- необходимость дополнительного устройства к ЭВМ
2. Файловый (табличный)
Случайные числа оформляются как таблицы и помещаются в виде файлов в ЭВМ. Файлы строятся на основе специальных справочников.
Достоинства:
- генерация действительно случайных хороших чисел
- требуется однократная проверка файла
- можно воспроизводить последовательность случайных чисел
Недостатки:
- огромное требование к ресурсам
- запас чисел ограничен
3. Алгоритмический (программный)
Используются алгоритмы.
Достоинства:
- требуется однократная проверка
- возможность воспроизведения последовательности случайных чисел
- малые вычислительные ресурсы
- не требуются дополнительные устройства
Недостатки:
- запас чисел ограничен периодом последовательности случайных чисел
- дополнительные вычислительные затраты по сравнению с другими двумя способами.
Алгоритмические генераторы случайных чисел
Все алгоритмы генераторов случайных чисел основаны на выборе следующего числа как функции от предыдущего случайного числа. А так как функция детерминирована, то случайности нет – псевдослучайные числа. Для того чтобы пользоваться такими алгоритмами используют специальные тесты. Тестами находят период последовательности случайных чисел.
Моделирование равномерных и нормальных распределений
Равномерный закон распределения:
Непрерывная случайная величина имеет равномерное распределение в интервале (а, b), если ее функция плотности имеет вид
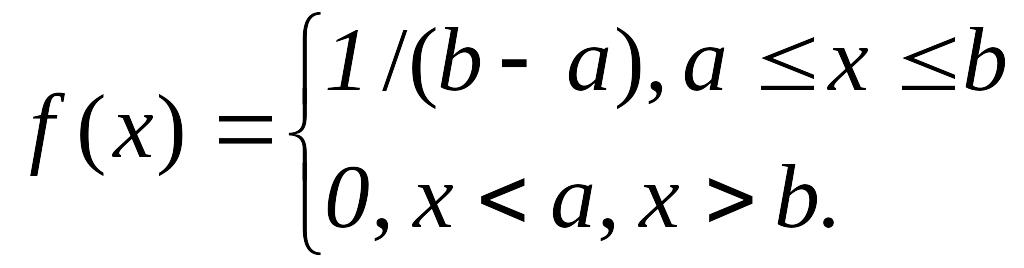
- На ЭВМ с n-разрядными числами вместо непрерывной совокупности равномерных случайных чисел интервала (0, 1) используют дискретную последовательность 2n случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.
- Наибольшее применение в практике моделирования нашли алгоритмы вида
xi+1 = F(xi),
представляющие собой рекуррентные соотношения, для которых начальное значение x0 и параметры функции F заданы, например
Xi+1 = λ Xi (mod M),
где λ, Xi , M - неотрицательные целые числа.
- Для реализации на ЭВМ наиболее удобно, когда М = р^k , где р - число цифр в системе счисления, принятой в ЭВМ (например, р = 2 для двоичной): k - длина разрядной сетки (например k = 32 для 32-разрядной ЭВМ). В этом случае вычисление остатка от деления на М сводится к выделению k младших разрядов делимого, а преобразование целого числа Xi в рациональную дробь из интервала (0, 1) осуществляется подстановкой слева от Xi двоичной запятой.
Нормальное распределение:
является одним из важнейших непрерывных распределений. Все методы базируются на использовании равномерно распределенных случайных чисел.
- Один из часто применяемых метод основан на центральной предельной теореме, которая гласит, что сумма независимых одинаково распределенных случайных чисел с математическим ожиданием am и среднеквадратическим отклонением σm образует асимптотически случайное число с нормальным законом распределения и математическим ожиданием a = N am и среднеквадратическим отклонением σ = σm√N , где N – число суммируемых чисел. Расчеты показывают, что уже при сравнительно небольших N (8, 12) сумма имеет распределение, близкое к нормальному.
Нормированное распределение с M(x) = 0, D(x) = 1 можно получить, воспользовавшись преобразованием yнорм = √12/N * (∑ xpавн – N/2).
В частности, при N=12 получим yнорм = ∑ xpавн – 6.