
Лаба_4_2
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА № 82
ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
|
доцент |
|
|
|
В.С. Блюм |
|
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
|
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4 |
|
Метод регрессии. |
по курсу: Интеллектуальные информационные системы |
|
|
|
|
РАБОТУ ВЫПОЛНИЛ
|
СТУДЕНТ ГР. № |
4616 |
|
|
|
А.В.Павлов |
|
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 2019
Цель работы: Метод регрессии.
Ход работы:
Создаем линейную регрессию и смотрим полученный результат. Линейная регрессия используется для создания взаимосвязи между двумя или несколькими переменные с помощью подгонки линейного уравнения к наблюдаемым данным.
Для простого примера возьмем исходные данные, а именно таблицу polynomial и сделаем регрессию
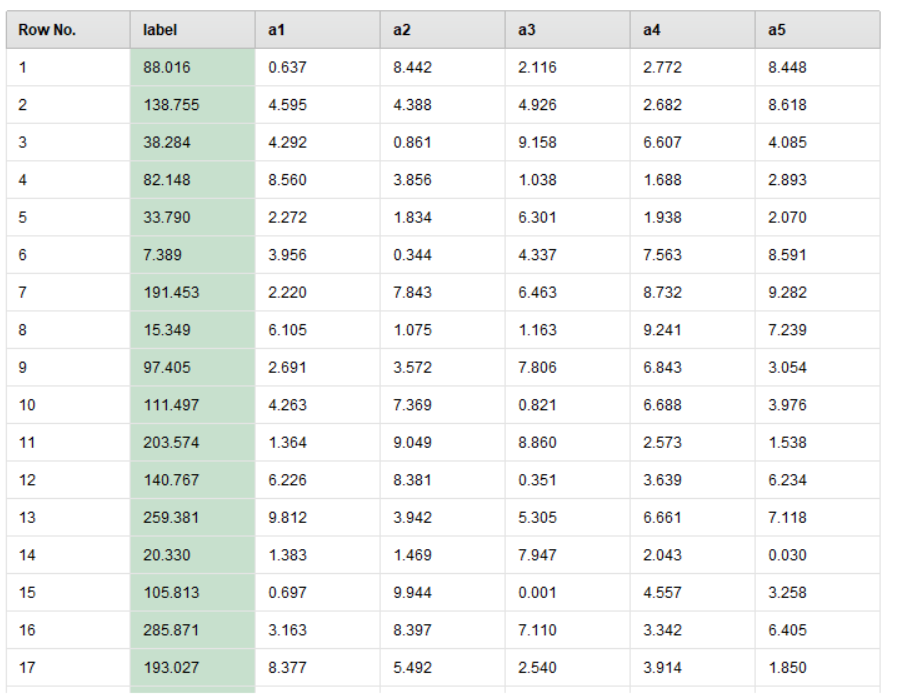
Рисунок 1 – Таблица polynomial
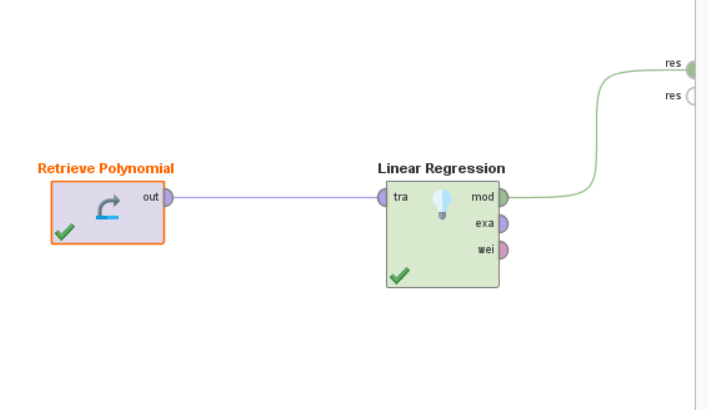
Рисунок 2 – Процесс

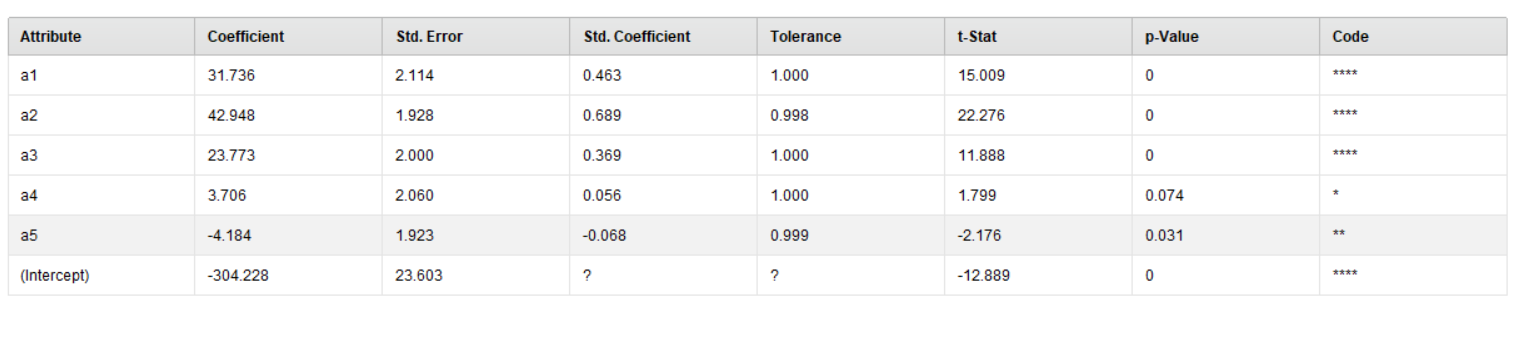
Рисунок 3 – Результат работы
Далее повторим тоже самое только уже для наших данных, а именно цен на квартиры в Москве
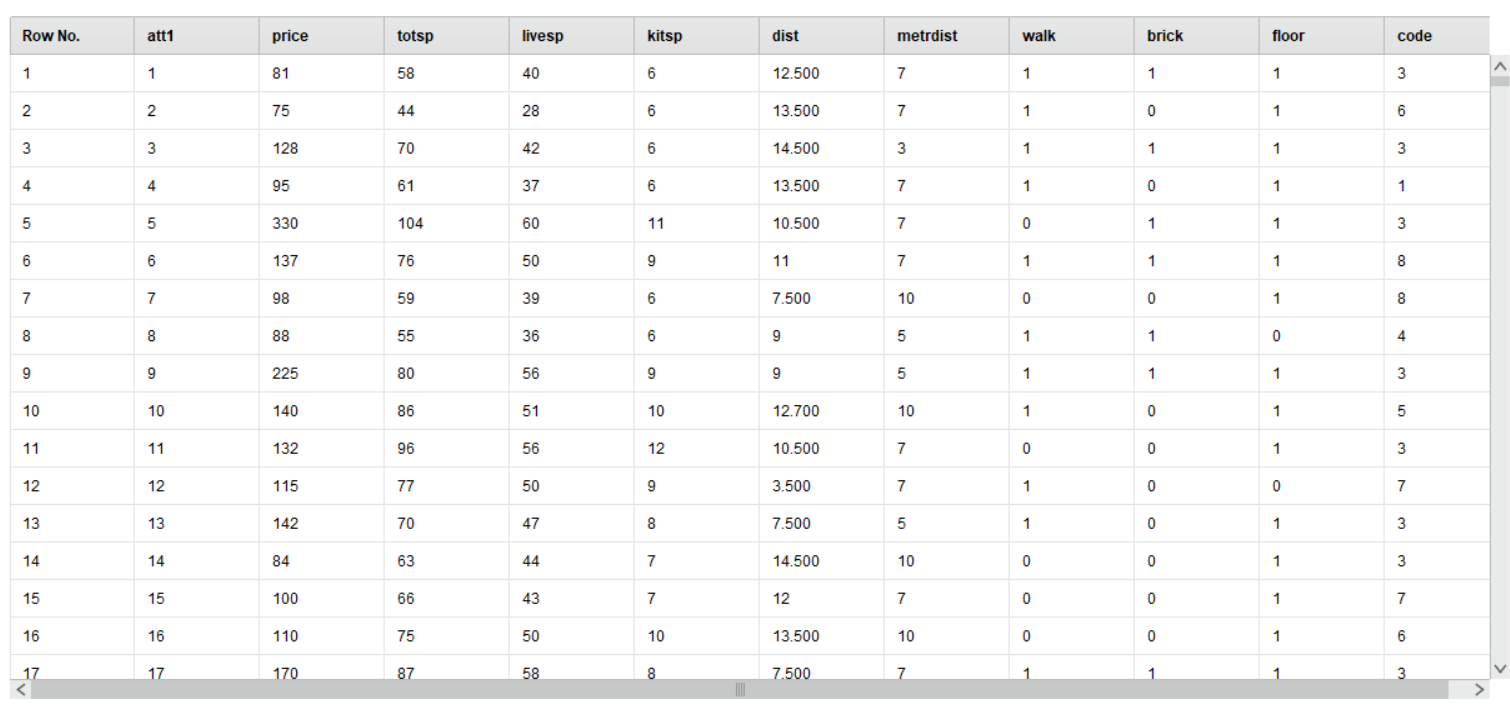
Рисунок 4 – Таблица цен недвижимости
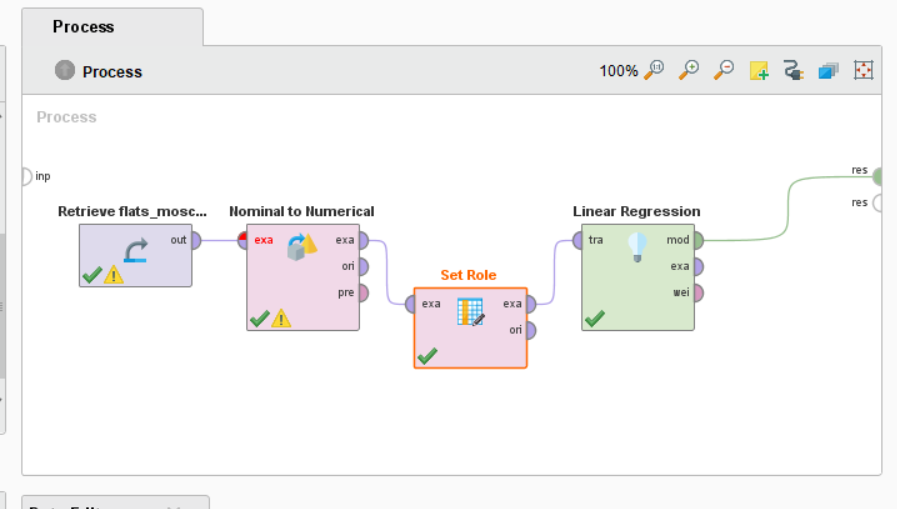
Рисунок 1 – Создание процесса
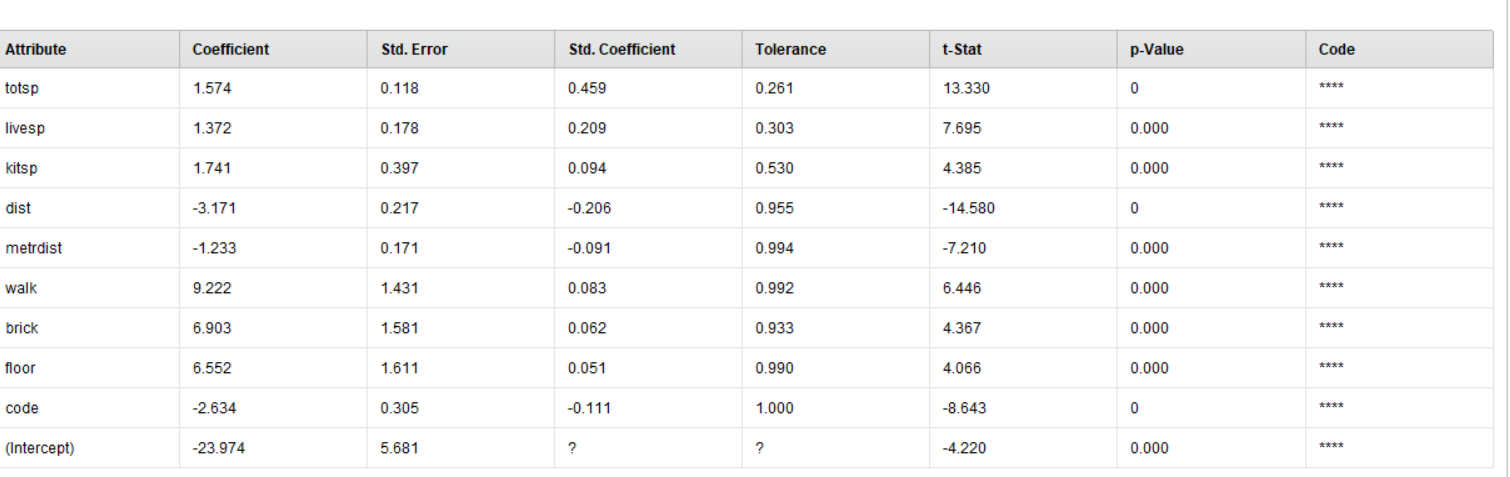
Рисунок 2 – Табличный результат
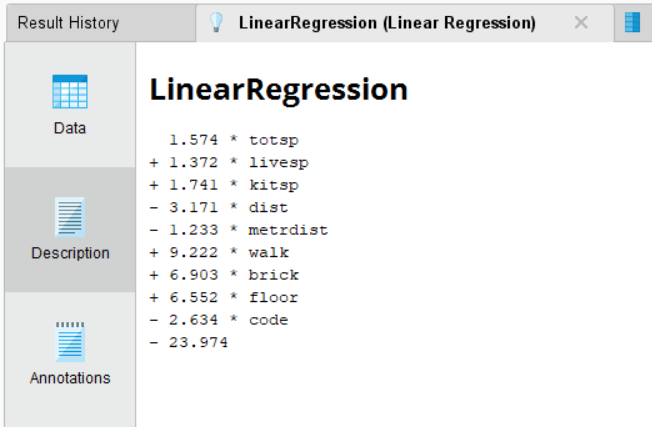
Рисунок 3 – Описательный вариант
Далее будем использовать полиномиальный тип регрессии для той же таблицы, а именно цен на квартиры. Полиномиальная регрессия является случаем множественной линейной регрессии.
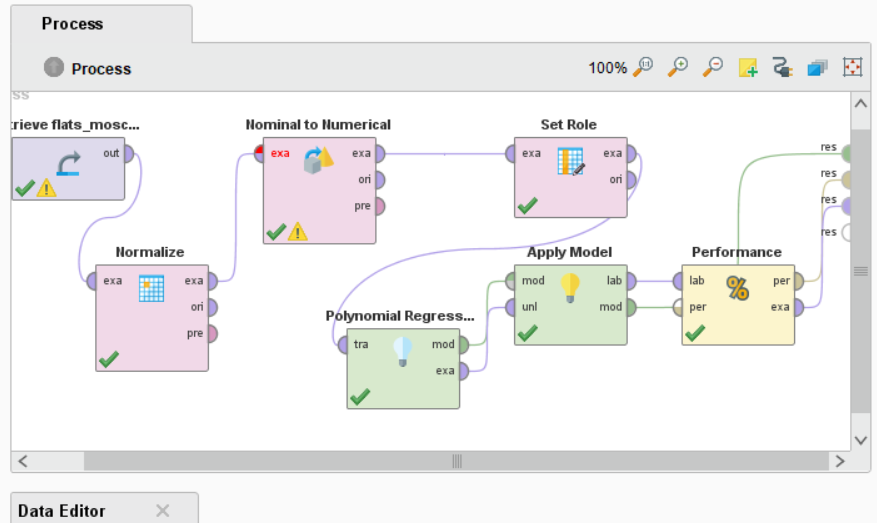
Рисунок 4 – Полиномиальная регрессия процесс
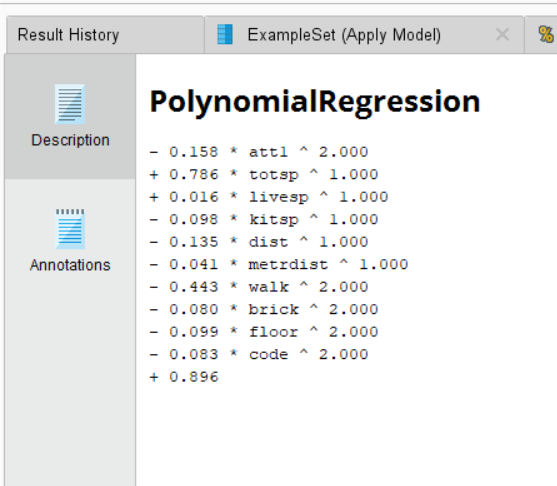
Рисунок 5 – Результат описания
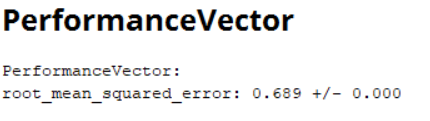
Рисунок 6 – Результат вектора
Вывод: В ходе лабараторной работы мы изучили типы регрессии, с помощью своих данных применили знания о регрессии и получили рассчитанный результат с помощью RapidMiner
Контрольные вопросы:
-
Regressio переводиться как обратное движение, возвращение
-
Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата
-
Линия регрессии — прямолинейное уравнение, отражающее взаимосвязь у и х, позволяющее исчислить ожидаемое значение у при заданном значении х. В необходимых случаях такие расчеты могут быть использованы при прогнозировании.
-
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю. если угловой коэффициент линии равен нулю, между x и y нет линейного соотношения: изменение x не влияет на y
