24. Принципы качества управления тех.Процессом

Основными хар-ми качества систем упр-ния яв-ся: устойчи

вость систем при определен

ном диапазоне настроек и качество регулирования в переходном и установившемся режимах. При желании улучшить качество систем, как правило, приближают систему к границе устойчивости. Поэтому при анализе систем управления в первую очередь оценивают структурную устойчивость и область устойчивости при варьирова нии настроек.

Если система устойчива, она отрабатывает возмущения и всегда с определенной точностью возвращает регулируемый параметр на заданное заданием значение.

Рассмотрим геометрическую интерпретацию устойчивости системы (см. рис. 20). Шарик, находящийся в вогнутой поверхности подобен системе автоматического регулирова-ния. При действии возмущения шарик из невозмущенного состояния (точка А1) перемещается в возмущенное состояние (точка А 2).

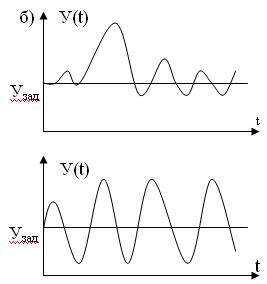
Рис. 20 - а) – геометрическая интеграция устойчивости системы автоматического регулирования; б) – переход-ные процессы соответственно устойчивой системы, соответ-ствующей вогнутой поверхнос-ти и неустойчивой системы, соответствующей выгнутой системы.

По определению Ляпунова система устойчива, если она от возмущенного состояния равновесия (точка А 2) перейдет в некоторую конечную область (точка А 3), окружающую невозмущенное состояние равновесие. Если разомкнем обратную связь системы регулирования, то выходная величина будет равна y(t) = x(t) ^. W_p ^. W_об, причем передаточная функция разомкнутой системы будет W_p ^. W_об (см. Рис. 21).

Передаточную функцию разомкнутой системы можно представить в виде ,

где – алгебраические

полиномы от Р.

Условием устойчивости разомкнутой системы – является отрицательный знак вещественной части корней характеристического управления D(P) = 0.

Для замкнутой системы справедливо следующее равенство.

Из равенства находим передаточную функцию замкнутой системы

Условием устойчивости замкнутой системы является отрицательный знак вещественной части всех корней характеристического уравнения D(р) + K(р) = 0.

Исследования устойчивости сводится таким образом, к определению знаков вещественной части корней характеристического уравнения, т.е. к вопросу распределения корней относительно мнимой оси в комплексной плоскости Р.

Существенным является поэтому выяснение правил, которые позволили бы минуя вычисления самих корней, ответить на вопрос, как распределены корни в комплексной полости относительно мнимой оси.

Правила, позволяющие определить расположение корней относительно мнимой оси, называются критериями устойчивости.

В настоящее время при решении вопроса об устойчивости используются алгебраические критерии: Рауса, Гурвица и частотные Михайлова, Найквиста.

Качество процессов управления.

Устойчивость САУ необходи-мое, но далеко недостаточное условие рационального выбора структуры и элементной базы системы.Для того, чтобы определить хорошо ли работает спроектированная система регулирования, прави-льно ли настроен регулятор, необходимы количественные критерии оценки качества процессов управления.

В теории управления принято оценивать качество процессов управления либо непосредст-венно по определенным из опыта или рассчитанным, кривым переходного процесса регулирования.

Прямые оценки качества систем – это оценки качества, полученные для кривой переходного процесса. Все остальные оценки качества называют косвенными.

Косвенные оценки качества связанны в основном с оценкой запасов устойчивости по амплитуде и по фазе.

Рассмотрим подробнее прямые оценки качества систем, которые используются в практике.

1. Оценка качества переход-ного процесса при возмущении вида ступенчатой функции.

2. Оценка качества установив-шихся процессов.

Оценками качества регулирования в переходном режиме являются: время переходного процесса Т_п.п., и величина перерегулирования.

Рис. 20 - Переходные процессы в системе автоматического регулирования а) – переход-ный процесс вызванный изменением задания; б) – пере-ходный процесс, обусловлен-ный изменением нагрузки Q.

Условием для определения Т_п.п. является окончание колебательных процессов в системе. Количественной оценкой окончания колебательных процессов принимается момент достижения параметром 5% отклонения от заданного заданием значения ∆m, либо величины ошибки в установившемся режиме.

Изменение величины ∆m существенно влияет на Т_п.п. Время снятия переходной характеристики при ∆m = 5% должно быть не менее трех постоянных времени объекта управления.

Величина перерегулирования σ определяется следующим выражением

, где ymax – максимальное отклонение регулируемой величины от задания (см. Рис.26).

Обычно считается система удовлетворительной по динамическим характеристикам если σ < 25%.

Оценка качества системы регулирования в установившемся режиме определяется:

1. Ошибкой, вызванной нечувствитель-ностью регулятора, люфтами в исполнительных механизмах, погрешностью датчиков и т.д.

2. Ошибкой, вызван-ной статизмом системы.

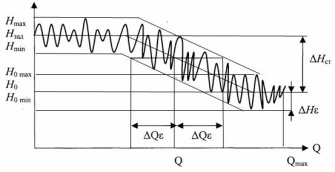
Рис. 27 - График изменения статической ошибки в зависимости от изменения нагрузки, например, изменения отбора пара в регуляторе уровня И.И. Ползунова

Статическая ошибка характерна для регуляторов прямого действия и других в основном пропорциональных регуляторах, в которых отсутствует интегральная составляющая.

Таким образом, в статических регуляторах максимальная ошибка регулирования равна (см. рис. 27)

г де Н_зад – задание регулятора, Н₀ – среднее установившееся значение уровня, Н_ε –величина нечувствительности регулятора.

Первое слагаемое является статической ошибкой, а второе вызванное нечувствитель-ностью регулятора.