8. Элементарные функции комплексного переменного

8.1. Показательная функция

Показательной функцией называется функция вида

.

Если z = x + iy, то показательную функцию можно определить так:

, (8.1)

откуда можно задать показательную функцию как функцию, модуль и аргумент которой равны

Если так определить показательную функцию, то операции над ней (умножение, деление, возведение в степень) будут выполнены по тем же правилам, что и операции над показательными функциями действительной переменной.

Например:

.

Аналогично и для других операций:

, .

Формула (8.1) позволяет вычислять значения показательной функции при любых комплексных показателях.

Например: 1) ;

2) .

Изучим и другие свойства показательной функции.

Периодичность. Показательная функция периодическая с периодом 2i:

.

Аналитичность:

.

Проверяя условия Коши – Римана , делаем вывод об аналитичности показательной функции

;

.

Эти условия выполняются на всей плоскости z, поэтому аналитическая на всей плоскости z.

Кроме того, , значит, отображение, производимое показательной функцией, является конформным на всей плоскости z.

Пример

Отобразить с помощью показательной функции семейства прямых

;

.

Решение

.

. Параметрические уравнения образа семейства этих линий на плоскости w имеют вид

Освобождаясь от параметра –y (возводя в квадрат и складывая), получим уравнение образа семейства линий в координатах u0v:

.

Это семейство окружностей радиуса .

Im z = by = b. Параметрические уравнения образа семейства этих линий на плоскости w имеют вид

Произведя преобразования, получим уравнение образа семейства линий Im z = b на плоскости w:

.

Это семейство лучей, выходящих из начала координат.

В частности, если b = 0, то действительная ось плоскости z отобразится в прямую

Так как , то при -  x   получим 0  u  . Это означает, что действительная ось плоскости z отобразится в положительную действительную полуось плоскости w (рис. 8.1).

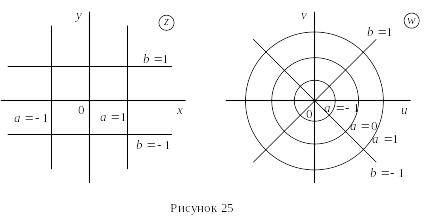
Р и с. 8.1

8.2. Логарифмическая функция

Логарифмическая функция определяется как функция, обратная показательной, т.е. число w называется логарифмом числа z, если и обозначается .

Найдем действительную и мнимую части этой функции.

Согласно определению

;

;

,

откуда

, или , , .

Получим формулу для логарифмической функции

. (8.2)

Из формулы (8.2) видно, что логарифмическая функция определена всюду кроме z = 0 и является многозначной (наличие 2k в мнимой части).

Введем понятие главного значения логарифмической функции. Это то значение, которое соответствует главному значению аргумента z. Его можно получить из (8.2) при k=0. Обозначается как ln z и выражается следующим соотношением:

. (8.3)

Найденное по формуле (8.3) значение логарифма определяется однозначно.

Пример

Найти общее и главное значение логарифма чисел: а) –1; б) 5+12i; в) –1+i.

Решение

а) ln (-1) = ln-1+i(arg(-1)+2k) = i+2ki = i(2k+1), ln (-1)= i.

б)

в) , .

Логарифмическая функция в смысле главного значения является аналитической во всей плоскости z кроме z=0 .