5. Метод хорд для решения уравнений

В качестве отрезка берется отрезок . Точка с₁ берется как точка пересечения с осью абсцисс прямой, проходящей через точки и . Укажем значение для c₁ в явной форме:

.

Из двух отрезков и выберем тот, на концах которого функция имеет разные знаки и этот отрезок примем за . Затем найдем точку по отрезку точно так же, как нашли точку по отрезку : это будет точка пересече-ния с осью абсцисс прямой, проходящей через точки и :

.

Затем в качестве отрезка берется тот из отрезков и , на концах которого имеет разные знаки и т.д. Через последовательность точек приближенное значение корня находится так же, как в п.1. Название метода происхо-дит из того, что конструируемые по ходу дела прямые являются хордами по отношению к графику функции.

6. Метод касательных для решения уравнений

Пусть = . Выберем тот край отрезка , на котором функция имеет тот же знак, что и ее вторая производная. В нашем примере на приведенной выше схе-ме - это точка b. Проведем через точку касательную к графику функции . Точку пересечения этой касательной с осью абсцисс и примем за точку c₁. Вот соответ-ствующая формула для рассматриваемого случая:

Нетрудно получить аналогичные формулы для случаев, когда знаки упомянутых выше значений иные. Важен принцип: касательная проводится к графику в той точке, где знак значения функции совпадает со знаком ее второй производной. После этого из двух отрезков и выберем тот, на концах которого функция имеет разные знаки и этот отрезок примем за . Затем найдем точку по отрезку точно так же, как нашли точку по отрезку и т.д. Через последователь-ность точек приближенное значение корня находится так же, как в п.1.

7. Интерполяционный многочлен Лагранжа и различные формы его записи

Будем исхожить из таблицы в предыдущем пункте. Построим по ней следующий многочлен:

.

Для ясности надо заметить, что в этой сумме - ( ) слагаемых, что в слагаемом № k в числи-теле ровно множителей и что каждый из них является многочленом степени n. Этот многочлен называется многочленом Лагранжа таблицы значений функции.

Вот его основные свойства:

1. это - многочлен степени ;

2) , т.е. многочлен Лагранжа имеет в точках те же значения, что

и функция ;

3) если фиксировать любое число то окажется выполненным неравенство

где на участке , т.е. число ограничивает производную го порядка функции .

8. Существует иной подход, именуемый равномерным приближением. При этом подходе тоже происходит замена значения на значение некоторой функции , причем оказывается возможным оценить ошибку этой подмены. Строится функ-ция следующим образом.

Для осуществления равномерного приближения должна быть задана не только таблица из п.1, но и некоторый класс функций G внутри которого и будет выделена функция . Введем величину

,

в которой числа берутся из таблицы в п.1, а числа для каждой функции из класса G предполагаются вычислимыми. Функция выбирается как доставляющая минимум величине . Эту функцию называют наилучшим равномерным приближением функ-ции из класса G. Конечно, как оценить разность в такой ситуации, - это от-дельная тема, тесно связанная как с природой класса G, так и с таблицей из п.1. Мы не затрагиваем здесь эту тему.

9. Метод наименьших квадратов.

Предположим, что класс G представляет собой множество всех многочленов степени не превосходящей некоторого конкретного числа m. Тогда задача равномерного приближения функций приобретает следующий вид:

среди многочленов найти такой, при котором ве-личина

принимает минимальное значение.

Для этого надо найти такие , при которых функция

принимает минимальное возможное значение, а это происходит тогда, когда равны нулю все ее частные производные:

это - система из m+1линейных алгебраических уравнений с m+1 неизвестными ; можно доказать, что эта система всегда совместна и определенна. Ее решение и есть искомый многочлен.

Распишем эту систему в традиционной форме, раскрыв скобки и приведя подобные

члены:

;

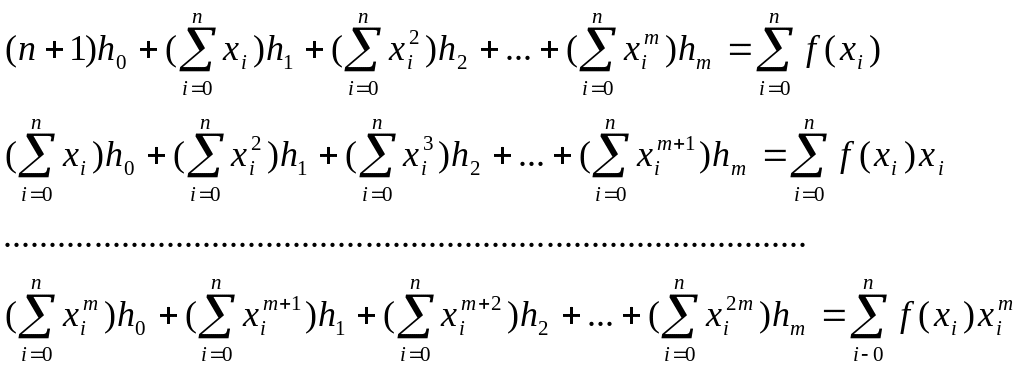включив процедуру решения систем линейных алгебраических уравнений теперь легко получить ответ.

10. Численное интегрирование функции одной переменной.

Требуется найти

с той или иной степенью точности. Известны три классических способа сделать это.

Способ № 1: метод прямоугольников. Отрезок разбивается на равных частей: длиной , где

.

Затем на каждом участке функция заменяется на константу , после чего искомый интеграл заменяется на интеграл от новой ступенчатой функции, т.е. на число

.

Можно доказать, что справедлива следующая оценка:

,

где - максимум модуля первой производной функции на отрезке .

Способ № 2: метод трапеций.

В этом методе искомый интеграл после разбиения отрезка на равные части заменяется на следующую сумму (суммируются площади трапеций, а не прямоугольников, как в предыду-щем случае):

,

где Можно доказать, что если - исходный обсуждаемый интеграл,то

,

где на отрезке .

Способ № 3: метод парабол. В этой ситуации отрезок разбивается на равных частей: , где . На участках , функцию заменяют на параболу, проходящую через точки и интегралом от этой параболы на участке заменяют интеграл от функции на этом же участке, после чего все эти интегралы суммируют и результаты принимают за интеграл от по всему отрезку . Полученная приближенная формула называется формулой парабол или формулой Симпсона. Вот ее окончательный

вид:

.

Если левую часть этого приближенного равенства обозначить через _I, а правую – через _S, то окажется выполненной следующая формула для оценки погрешности:

,

где - максимум на интервале четвертой производной функции

11. Метод Эйлера численного решения обыкновенного дифференциального уравне-

ния.

1й шаг. Фиксируем точность, с которой нужно найти значение . Обозначим это число через . Поясним, что это означает, что числа, отличающиеся меньше, чем на , считаются одинаковыми.

2й шаг. Фиксируем произвольное и разделим отрезок на равных частей: , где .

3й шаг. Построим последовательность чисел

,

в которой, напомним, . Обозначим через .

4й шаг. Заменим на и повторим шаги 2 и 3. Полученное число (т.е. последнее из вычисляемых на шаге 3) обозначим теперь через _V.

5й шаг. Если окажется, что числа _U и _V отличаются друг от друга меньше, чем на , то число считается найденным и равным _V. В противном случае переобо-значим _V через _U и вернемся к шагу 4.

Можно доказать, что когда функция из имеет непрерывные частные производные, описанный процесс обязательно конечен и ответ находится действительно с любой наперед заданной точностью.