1. Метод простых итераций

| Напомним, что здесь А - матрица системы, B - столбец свободных членов, а X -столбец неизве-стных.

Преобразуем систему к другому виду, выражая все неизвестные через самих себя,

Вот пример: ;

из первого уравнения получим из второго уравнения следовательно, при таком преобразовании

Пусть - столбец из n чисел, записанный ради экономии места в виде строки, заданный для каждого k=1,2,3,... . Пусть, далее, имеется столбец Назовем рас-стоянием от до число

ясно, что - числовая последовательность; если эта числовая последова-тельность стремится к нулю, то говорят, что столбцы стремятся к столбцу Z или что Z является пределом последовательности .

(1) если , то процесс итераций сходится к решению системы (3.1.1);

(2) если , то процесс итераций сходится к решению системы

2. Метод Зейделя

Метод Зейделя состоит в том, что итерации осущест-вляются несколько иначе. А именно, распишем равенство в виде обычных числовых равенств:

согласно этим равенствам, числа отыскиваются через числа Зейдель предложил отыскивать по , используя те же самые фор-мулы. Иными словами, в итерациях по Зейделю учитываются уже найденные значения прибли-жений. Сформулируем окончательно метод Зейделя: последовательность итераций строит-ся по формулам:

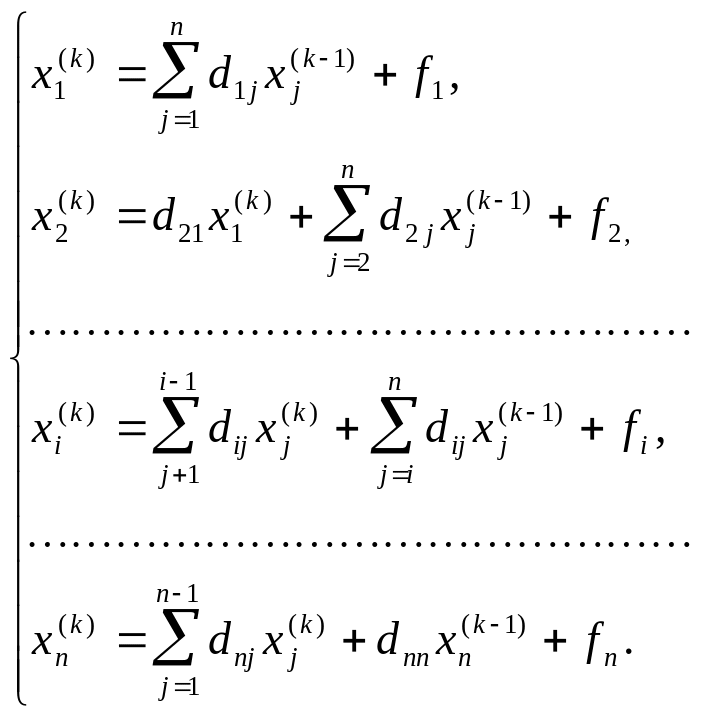
Вопрос о сходимости процесса итераций к решению решается здесь так же, как и выше в случае простых итераций: всё зависит от матрицы D. Условия здесь те же, что и выше.

3. Метод итераций для решения уравнений

Мы искали решения систем линейных уравнений разными способами, в том числе - методом итераций. В общем случае схему итераций можно также воспроизвести. А именно, предположим, что тождественными преобразованиями данную в начале этого пункта систему уравений удалось представить в виде:

Тогда, начав с произвольного набора , можно организовать итерации где . В случае линейных систем урав-нений мы сообщали условия, которые должны выполняться для того, чтобы указанный процесс итераций приводил именно к решению данной систе-мы уравнений. В общем случае такие усло-вия формулируются в существенно более сложных терминах - якобианах. Мы пока оставляем за пределами нашего курса этот вопрос.

4. Метод деления отрезка пополам для решения уравнений

Отсюда возникает простая методика приближенного поиска корня, отделенного в интервале (a,b): надо построить последовательность точек по следующему правилу: затем из двух интервалов (a,c1) и (c1,b)­ выбирается тот, на концах которого имеет разные знаки и его середина принимается за ; обозначим кон-цы этого интервала (у которого - середина) через (a2,b2), а затем выберем ту из его половин, на концах которой имеет разные знаки. Пусть (a3,b3) - эта половина и - середина этого отрезка и т.д. Доказывается, что построенная последовательность сходится к корню уравнения (3.3.1). Если с самого начала задается некоторая точность вычислений, то на практике построение последовательности прерывается тогда, когда два раза подряд получаются одинаковые с заданной точностью числа. Это последнее перед прерыванием построения последовательности число и при-нимается за приближенное с заданной степенью точности значение корня. Описанный метод уточнения корня называется методом деления отрезка попо-лам.