Числовые множества. Ограниченное множество. Принцип верхней грани. Супремум и инфимум.

Геометрически множество действительных чисел R изображается точками числовой прямой. Между точками числовой прямой и множеством действительных чисел существует взаимно однозначное соответствие, т.е. каждой точке числовой прямой соответствует действительное число и наоборот. Множество всех действительных чисел будем называть числовой прямой и обозначать символом (-) или R. Приведем примеры часто используемых числовых множеств. [a,b]={x  R, a  x  b} —отрезок (a,b) = {x  R, a <x <b } — интервал (a,b]= {x  R, a <x  b } — полуинтервал [a,b) = {x  R, a  x < b } — полуинтервал

Определение. Окрестностью точки x называется любой интервал, содержащий эту точку.

Окрестность точки x будем обозначать следующим образом U(x).

О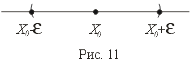 пределение. U_(x₀) эпсилон окрестностью точки x₀ называется интервал длины 2 с центром в точке x₀

|x-x₀| < 

Определение. Расстоянием в R между x и y называется  (x,y) = |x-y|.

Определение (ограниченное множество). Множество X называется ограниченным сверху (снизу), если для всех элементов из X, существует такое число a, что x  a (x  a). Множество X называется ограниченным, если найдутся a и b:  x  X, a  x  b, x  [a,b].

Эквивалентное определение ограниченного множества можно сформулировать следующим образом.

Определение. Множество X ограничено, если существует такое число c>0, что для всех x X выполнено неравенство |x|  c.

Приведем примеры, иллюстрирующие данные понятия.

1. Множество N натуральных чисел ограничено снизу и не ограничено сверху.

2. Любой конечный отрезок [a,b] или интервал (a,b) ограничен.

3. Числовая прямая R есть множество, не ограниченное ни сверху, ни снизу.

Определение. Элемент c  X называется максимальным (минимальным), если  x  X, x  c (x  c) .

Рассмотрим следующие примеры

1. Множество целых чисел Z = {...,-3,-2,-1,0,1,2,3,...}

не имеет ни максимального элемента, ни минимального.

2. Множество натуральных чисел N = {1,2,3,...}

имеет минимальный элемент, равный единице, но не имеет максимального.

3. Отрезок [a,b] имеет как минимум, равный a , так и максимум, равный b.

4. Интервал (a,b) не имеет ни максимума, ни минимума.

Пусть множество X ограничено сверху. Тогда оно имеет бесконечное множество верхних граней. Действительно, если S – верхняя грань X, то и любое число S'>S также является верхней гранью. Наименьшая из верхних граней множества X называется точной верхней гранью множества X. Обозначается точная верхняя грань через sup X (супремум).

Учитывая вышесказанное, можно дать эквивалентное определение точной верхней грани.

Определение (определение точной верхней грани). Число S называется точной верхней гранью множества X (S = sup X), если выполняются следующие свойства:

1. x S  x  X ;

2. >0  x_>S-.

Аналогично определяется и точная нижняя грань, которая обозначается inf X (инфимум).

Определение (определение точной нижней грани). Число I называется точной нижней гранью множества X (I = inf X), если выполняются следующие свойства:

1. x I  x  X ;

2. >0  x_<I+.

В случае, когда множество X имеет максимум или минимум, то они совпадают соответственно с sup X и inf X. Если множество X не ограничено сверху, то будем считать, что sup X = . Аналогично, если множество не ограничено снизу, то inf X = -. Проиллюстрируем эти понятия на примерах.

1. Для множества натуральных чисел N inf N = min N = 1, sup N = 

2. X 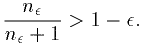= {n/n+1, n  N }={1/2,2/3,3/4,....} inf X = min X = 1/2, sup X = 1. Отметим, что 1 не принадлежит данному множеству. Покажем, что sup X = 1 на основании определения. Очевидно, что .

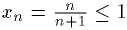3. Проверим, что  >0  x_>1-. Для этого решим неравенство

Отсюда . Таким образом при любом  >0  n_, которое можно найти. Задавая  можно определить n, зависящее от .

Теорема (принцип верхней грани). Всякое не пустое ограниченное сверху подмножество множества действительных чисел имеет единственную точную верхнюю грань.

Доказательство. Y = {y  R:  x  X, x  y } — множество верхних границ. По аксиоме полноты  c  R, x  c  y т.е. c  Y, c = min Y  c = sup X.

Т еорема. Всякое не пустое ограниченное снизу подмножество множества действительных чисел имеет единственную точную нижнюю грань.

Ограниченность функции.

Функция , называется ограниченной на множестве X, если существуют числа m и M такие, что . Число называется точной нижней гранью функции f, а число - точной верхней гранью функции f на множестве M. Разность M₀ - m₀ называется колебанием функции f на множестве X. Если функция f: X → R имеет конечный предел в точке , то она ограничена в некоторой окрестности этой точки.

Ограниченность последовательности.

Последовательность {x_n} называется ограниченной снизу (сверху), если существует такое число C, что все члены последовательности удовлетворяют условию x_n ≥ C (x_n ≤ C). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной. Можно показать, что если последовательность имеет предел, то она ограничена. Заметим, что не всякая ограниченная последовательность является сходящейся. Примером расходящейся ограниченной последовательности может служить последовательность {x_n}: x_n = (–1)ⁿ.

Окрестность.

Окрестностью точки называют любой интервал, содержащий эту точку; ε-окрестностью (ε > 0) точки называется интервал , т. е. множество чисел х, удовлетворяющих условию Различают следующие виды промежутков: 1) замкнутый промежуток (отрезок, сегмент): ; 2) открытый промежуток (интервал): (иногда для интервала используют обозначение ); 3) полуоткрытые промежутки: , (в других обозначениях и соответственно); 4) бесконечные промежутки (лучи, полупрямые): , , , , (числовая прямая).

Предельная точка множества.

Пусть . Число называется предельной точкой множества X, если . Из определения следует, что любая окрестность точки x₀ содержит точку из множества X, отличную от x₀. Сама точка x₀ может принадлежать, а может и не принадлежать множеству X. Значение +∞ есть предельная точка множества X, если . Значение -∞ предельная точка множества X, если . Точка , не являющаяся предельной точкой множества X, называется изолированной точкой множества X, т. е. . Число называется предельной точкой множества , если из этого множества можно выделить последовательность (x_n) различных точек, сходящуюся к x₀.