1.

Для квадратной матрицы можно вычислить число, которое называется определителем. Определитель второго порядка вычисляется по схеме крест, а определитель третьего порядка - по схеме треугольников.

2.

Для решения этой системы вычислим определители:

Если d0, то система имеет единственное решение: x=d_x/d, y=d_y/d. Если d=0, а dx0 или d_y0 то система не имеет решений. Если d=d_x=d_y=0, то одно из уравнений системы следствие другого. В этом случае его надо отбросить и решать оставшееся уравнение.

8.

Прямая на плоскости и различные способы её задания.

Ax + By + C = 0	A2 + B2  0	Общее уравнение прямой. (A,B) - вектор, перпендикулярный прямой.
y = kx + b		Уравнение прямой с угловым коэффициентом k
	a0, b0	Уравнение прямой в отрезках a и b
	a0, b0	Уравнение прямой по точке (x0,y0) и направляющему вектору (a,b)
	x2x1, y2y1	Уравнение прямой по двум точкам (x1,y1) и (x2,y2)
		Уравнение прямой по двум точкам (x1,y1) и (x2,y2)
		Параметрическое уравнение прямой по точке (x0,y0) и направляющему вектору (a,b)

9.

Виды уравнения прямой в пространстве:

		Общее уравнение прямой
	a0, b0, c0	Уравнение прямой по точке (x0,y0,z0) и направляющему вектору (a,b,c)
	x2x1, y2y1, z2z1	Уравнение прямой по двум точкам (x1,y1,z1) и (x2,y2,z2)
		Параметрическое уравнение прямой по точке (x0,y0,z0) и направляющему вектору (a,b,c)

10.

Виды уравнения плоскости в пространстве:

Ax + By + Cz + D = 0	A2+B2+C20	Общее уравнение плоскости. (A,B,C) - вектор, перпенди-кулярный плоскости.
A(x-x0)+B(y-y0)+C(z-z0)=0	A2+B2+C20	Уравнение плоскости по точке (x0,y0,z0) и ортогональ-ному вектору (A,B,C)
z = kxx + kyy + b		Уравнение плоскости с угло-выми коэффициентами kx и ky
	a0, b0, c0	Уравнение плоскости в отрезках a, b и c
		Уравнение плоскости по трём точкам (x1,y1,z1), (x2,y2,z2) и (x3,y3,z3)

11 - 14. Эллипс. Гипербола. Парабола. Окружность.

Линии второго порядка.

	(x-x0)2+(y-y0)2=R2	(x0,y0) - центр, R - радиус
Окружность	x2+y2+2Ax+2By+C=0	общее уравнение окружности, A2+B2>C
Парабола	y2=2px или x2=2py	p - расстояние между фокусом и директрисой
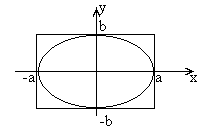
Эллипс	, a>b	a и b - полуоси, расстояние от центра до фокусов c= , =c/a<1 эксцентриситет.
	, a<b	a и b - полуоси, расстояние от центра до фокусов c= , =c/b<1 - эксцентриситет.
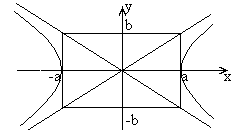
Гипербола		a - действительная полуось, b - мнимая полуось, расстояние от центра до фокусов c= , эксцентриситет =c/a>1.
		a - мнимая полуось, b - действи-тельная полуось, расстояние от центра до фокусов c= , эксцентриситет =c/b>1.

Парабола y2=2px (p>0)	y x
Эллипс (a>b)
Гипербола

15.

Функцией (y = f(x)) называется соответствие между двумя числовыми множествами при котором каждому элементу первого множества (область определения) соответствует единственный элемент второго множества (множество значений). Функции могут быть заданы формулами, таблицами или графиками.

17.

Свойства предела последовательности:

1) 2)

3) 4)

5) 6) Число е: .

18.

Пусть дана последовательность: a₁,a₂,a₃,...,a_n,..., тогда формальная запись a₁+a₂+a₃+...+a_n+... или короче называется числовым рядом. Пусть S_n= a₁+a₂+a₃+...+a_n. Если существует , то говорят, что ряд сходится, а этот предел называется суммой ряда. Если ряд сходится, то (необходимый признак сходимости).

19.

Степенным называется ряд вида: , где a₀,a₁,a₂,...,a_n,... - числовая последовательность. Радиус сходимости степенного ряда R= , при этом при |x|<R ряд сходится, а при |x|>R расходится.

20.

Функция f(x) называется непрерывной в точке a, если . Функция f(x) называется непрерывной на промежутке, если она непрерывна во всех точках этого промежутка.

21.

Производной называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю:

Основные свойства производных (правила дифференцирования):

1) c=0

2) (yz)=yz

3) (yz)=yz+yz, в частности (cy)=cy

4) , в частности

5)

6) (f(g(x)))=f(g(x))g(x), в частности (f(ax+b))=af(ax+b)

Дифференциалом функции называется выражение dy=ydx.

23.

Если при переходе через точку x₀ вторая производная f(x) меняет знак, то в этой точке перегиб. Это оформляется например так:

- + + - - x      перегиб перегиб на рисунке указаны знаки второй производной f(x)

24.

Если f(x)>0, то f(x) возрастает, а если f(x)<0, то f(x) убывает.

Если при переходе через точку x₀ производная f(x) меняет знак, то в этой точке экстремум. Это оформляется например так:

- + + - - x min max на рисунке указаны знаки производной f(x)

25.

Правило Лопиталя: если или , то

26.

Первообразной для функции f(x) называется такая функция F(x), что F(x) = f(x). Неопределённым интегралом называется множество всех первообразных. Он обозначается так: f(x)dx. В этой записи f(x)dx называется подынтегральным выражением, а f(x) - подынтегральной функцией. При этом можно записать f(x)dx=F(x)+C, где F(x) - одна из первообразных, то есть F(x)=f(x).