3. Основные теоремы линейного программирования

Для обоснования методов решения задач линейного программирования сформулируем ряд важнейших теорем, опуская их аналитические доказательства. Уяснить смысл каждой из теорем поможет понятие о геометрической интерпретации решения ЗЛП, данное в предыдущем подразделе.

Однако сначала напомним о некоторых понятиях, важных с точки зрения дальнейшего разговора.

Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными).

Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

В частном случае, когда в систему ограничений входят только две переменные x₁ и x₂, это множество можно изобразить на плоскости. Так как речь идет о допустимых решениях (x₁, x₂ ≥ 0), то соответствующее множество будет располагаться в первой четверти декартовой системы координат. Это множество может быть замкнутым (многоугольник), незамкнутым (неограниченная многогранная область), состоять из единственной точки и, наконец, система ограничений-неравенств может быть противоречивой.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений.

Из теоремы 2 можно сделать вывод о том, что единственность оптимального решения может нарушаться, причем, если решение не единственное, то таких оптимальных решений будет бесчисленное множество (все точки отрезка, соединяющего соответствующие угловые точки).

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений, и наоборот.

Следствием из теорем 2 и 3 является утверждение о том, что оптимальное решение (оптимальные решения) задачи линейного программирования, заданной (или приведенной) ограничениями-уравнениями, совпадает с допустимым базисным решением (допустимыми базисными решениями) системы ограничений.

Таким образом, оптимальное решение ЗЛП следует искать среди конечного числа допустимых базисных решений.

На этом шаге мы рассмотрим представление задачи линейного программирования в канонической форме. 

    Если математическая модель задачи линейного программирования имеет вид:

то говорят, что задача представлена в канонической форме.

    Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.

    Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:

• если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;

• если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;

• если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;

• если некоторая переменная x_j не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными: x₃ = x₃⁺ - x₃^-, где x₃⁺, x₃^- ≥ 0.

    Пример 1. Приведение к канонической форме задачи линейного программирования:

min L = 2x₁ + x₂ - x₃; 2x₂ - x₃ ≤ 5; x₁ + x₂ - x₃ ≥ -1; 2x₁ - x₂ ≤ -3; x₁ ≤ 0; x₂ ≥ 0; x₃ ≥ 0.

   Введем в каждое уравнение системы ограничений выравнивающие переменные x₄, x₅, x₆. Система запишется в виде равенств, причем в первое и третье уравнения системы ограничений переменные x₄, x₆ вводятся в левую часть со знаком "+", а во второе уравнение переменная x₅ вводится со знаком "-".

2x₂ - x₃ + x₄ = 5; x₁ + x₂ - x₃ - x₅ = -1; 2x₁ - x₂ + x₆ = -3; x₄ ≥ 0; x₅ ≥ 0; x₆ ≥ 0.

   Свободные члены в канонической форме должны быть положительными, для этого два последних уравнения умножим на -1:

2x₂ - x₃ + x₄ = 5; -x₁ - x₂ + x₃ + x₅ = 1; -2x₁ + x₂ - x₆ = 3.

   В канонической форме записи задач линейного программирования все переменные, входящие в систему ограничений, должны быть отрицательными. Допустим, что x₁ = x₁' - x₇, где x₁' ≥ 0, x₇ ≥ 0.

   Подставляя данное выражение в систему ограничений и целевую функцию и, записывая переменные в порядке возрастания индекса, получим задачу линейного программирования, представленную в канонической форме:

L_min = 2x₁' + x₂ - x₃ - 2x₇; 2x₂ - x₃ + x₄ = 5; -x₁' - x₂ + x₃ + x₅ + x₇ = 1; -2x₁' + x₂ - x₆ + 2x₇ = 3; x₁' ≥ 0; x_i ≥ 0, i=2, 3, 4, 5, 6, 7.

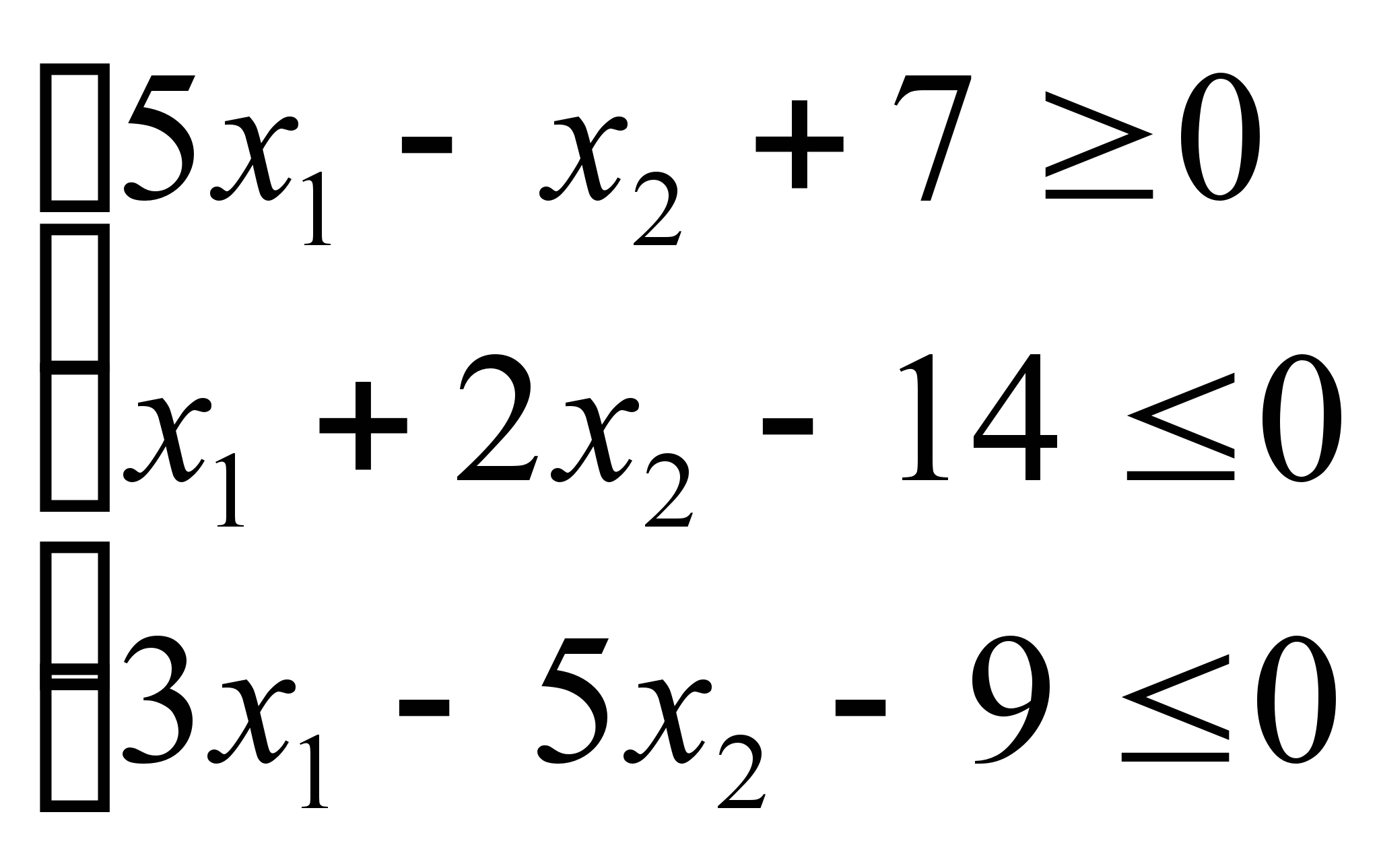12) 1. Графический метод решения задач линейного программирования. Задание: 1.Построить многоугольник решений. 2.Найти координаты вершин области. 3.Построить вектор   и  . 4.Найти   и  .  - целевая функция (1)  - ограничения функции (2)  (3) Решение: