24 §1 Цепи Маркова

1.1 Основные понятия.

В этой главе мы будем рассматривать некоторую систему ξ(t), которая в любой момент времени может находиться в одном из состояний S₁, S₂, …, S_k, и ξ (t) – это номер состояния, в котором система находится в момент t. Причём состояние системы отслеживается только в отдельные моменты времени {0, t, 2t, 3t,…}. В эти моменты времени система может переходить из одного состояния в другое. Т.е. время в этой модели дискретно.

Пример 1. Рассмотрим состояния, в которых может находиться студент:

S₁ – студент учится и не получает стипендию;

S₂ – студент учится и получает стипендию;

S₃ – студент отчислен.

Состояние студента может меняться после сессии раз в семестр, т.е. шаг t в примере – семестр, и здесь t – номер семестра.

Рассмотрим вероятность: P{ξ(t₁) = i₁ , ξ(t₂) = i₂ ,…, ξ(t_r) = i_r }.

Определение 1. Случайный процесс называется однородным (стационарным) или стандартным, если для любых t₁, t₂ … и T>=0 выполняется равенство:

(1.1) P{ξ(t₁) = i₁ ,…, ξ(t_r) = i_r } = P{ ξ(t₁ + T) = i₁ ,…, ξ(t_r + T) = i_r} , т.е. вероятность перехода из состояния i₁ с состояние i_r за время T  зависит только от величины T и не зависит от положения интервала на временной оси. В дальнейшем мы будем изучать только однородные (стационарные) процессы.

К примеру, стандартным процессом можно считать колебания курсов валют на небольшом отрезке времени.

Обозначим

(1.2) p_ij(t) = P{ξ(t) = j / ξ(0) = i} – вероятность перейти из состояния i в состояние j за t шагов.

Определим также

(1.3) P_ij = P_ij (1) – вероятность перейти из состояния i в состояние j за один шаг.

Определим также распределение вероятностей в начальный момент времени:

(1.4) p_i⁰ = P{ξ(0) = i}

Определение 2. Однородный процесс с дискретным временем называется Марковским или Марковской цепью с дискретным временем, если выполняется равенство:

(1.5) 

 

Утверждение 1. (Марковское свойство). Пусть дана Марковская цепь с дискретным временем, тогда справедливо равенство:

(1.6) P{ξ(t) = i_t / ξ(t–1) = i_t-1,ξ(t–2) = i_t-2 ,…, ξ(0) = i₀} = P{ξ(t) = i_t / ξ(t–1) = i_t-1}

Смысл: P(будущее/настоящее и прошлое) = P{будущее/настоящее}, т.е. в Марковских цепях будущее не зависит от прошлого, оно зависит только от настоящего. Такие системы ещё называются системами без памяти.

Часто Марковскую цепь удобно задавать при помощи графа переходов. При построении такого графа каждому состоянию ставится в соответствие вершина. Если из состояния s_i система переходит в состояние s_j  с ненулевой вероятностью  , то из вершины, соответствующей s_i, проводится стрелка в вершину s_j, помечаемая величиной  ; если  , то стрелку не проводят.

 

1.2 Матрицы переходов.

Определим матрицу переходов за n шагов (1.7) и матрицу переходов за один шаг (1.8) следующим образом:

 (1.7)      (1.8)

 

Пример 2. Воспользуемся состояниями студента из Примера 1. Из многолетнего опыта известно, что матрица переходов за один шаг:

Пусть начальное распределение: P⁰= (0,6; 0,4; 0). Найти вероятность того, что студент получает стипендию в течении двух первых семестров.

Решение: Надо найти: P{ξ(1) = 1, ξ(2) = 1} = {1.7} = P₁⁰  P₁₁  P₁₁ = 0,4 0,4 0,79.

 

Утверждение 2. Пусть дана Марковская цепь с дискретным временем с состояниями S₁ … S_k, тогда справедливо равенство:

(1.9)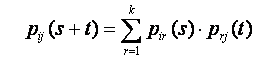

Доказательство: Формула полной вероятности:  . Обозначим через  A = {система перешла из состояния i в состояние  j за (s + t) шагов}, H_r = {система перешла из состояния i в состояние  r за S шагов}.

P(A) = P_{i j}(s + t) (*)

P(H_r) = P_{i r}(s) (* *)

P(A / H_r) = P_{r j}(t) (* * *)

Подставим (*), (**), (***) в формулу полной вероятности и получим (1.9)

 

Теорема 1. (Основное свойство Марковских цепей с дискретным временем):

(1.10) P(n) = Pⁿ, где слева матрица перехода за n шагов, справа – матрица перехода за 1 шаг.

 

Утверждение 3. Пусть дана Марковская цепь с состояниями S₁ … S_k, заданная матрицей переходов P, и задано начальное распределение вероятностей p⁰=(p₁⁰ ,p₂⁰ ,…, p_k⁰). Распределение вероятностей через n шагов можно вычислить по формуле:

(1.11)  , где p_i(n) = P{ξ(n) = i} – вероятность находиться в момент времени n в состоянии i.

 

Пример 3. На некотором острове в Северном море 30% женщин рыжих. Известно, что у рыжей матери  с вероятностью 0,6, а у не рыжей матери с вероятностью 0,2 рождается рыжая дочь. Найти вероятность того, что у не рыжей бабушки будет рыжая внучка.

Решение: Опишем процесс наследования цвета при помощи Марковской цепи. Составим матрицу переходов за 1 шаг, введя состояния: S₁ – рыжая,  S₂ – не рыжая, тогда матрица переходов за один шаг, где шаг – одно поколение:

Начальное распределение имеет вид: P₁⁰ = 0,3;   P₂⁰ = 0,7. Надо найти P_{2 1}(2). По теореме 1

=> P₂₁ = 0,28

В условиях этой же задачи найдем вероятность того, что у случайно выбранной женщины будет рыжая внучка. Обозначим события: H₁ – бабушка рыжая, H₂ – бабушка не рыжая. Тогда

P{рыжая внучка}=  P(H₁) * P₁₁(2) + P(H₂) * P₂₁(2) =

= 0,3 * 0,44 + 0,7 * 0,28 = 0,132 + 0,196 = 0,328

Решить эту задачу можно другим способом, если воспользоваться Утверждением 3, тогда надо найти: 

Нам надо p₁(2)=0,328.