Доказательство:

Запишем выражение

в виде:

Используя для этого выражения формулу  ,

получим

.

На основании теоремы о допустимости решения

-задачи,

получаем,что  целое.

Величины  ,   - целые по определению, следовательно,

получаемое в результате число

тоже является целым.

Покажем, что  .

При доказательстве, воспользуемся методом от противного.

Рассмотрим ситуацию, где  .

Отсюда выражение .

По определению дробной части

По условию теоремы есть допустимое решение (оно и рассматривается во

всей теореме)

-задачи, поэтому  .

Значит,

.

.

Тогда должно выполняться следующее неравенство:

.

Из предположения отрицательности   сразу же получаем   - нецелое.

А так как это противоречит факту, полученному ранее, то полученное противоречие и доказывает теорему.

Следствие. Любое оптимальное решение    -задачи, не являющееся допустимым решением  -задачи, не удовлетворяет условию правильного отсечения (2.1).

Доказательство:

Пусть   - оптимальное решение  , и некоторая компонента плана дробная.

Покажем, что   не удовлетворяет условию отсечения. Поскольку план оптимален, все небазисные переменные     равны нулю. Поэтому   С учетом того, формула 2.11 при базисной дробной компоненте имеет вид:

,

что противоречит условию неотрицательности  .

Последовательность   - задач пометим индексом  , соответствующим номеру итерации в последовательном приближении к решению исходной  -задачи, и обозначим . При этом  -задача соответствует задаче без требования целочисленности, т.е.  -задаче.

Переменную  , которая определяется дополнительным линейным ограничением (2.1) и строится по некоторой нецелочисленной координате оптимального решения  -задачи обозначим   (в дальнейшем это обозначение при решении задач не понадобится, достаточно обозначения

через  )

Алгоритм метода Гомори № 1

1. Решим

   -задачу методом последовательного улучшения плана.

2. Если все базисные компоненты оптимального решения    -задачи

   целые, то

   и есть решение

   -задачи.

3. Если некоторая компонента оптимального решения    -

   задачи

4. нецелая, то переходим к п.2.

5. Если в оптимальном плане единственная компонента нецелая,то дополнительное ограничение (2.1). строится по этой координате.

Если нецелых компонент в плане более одной, то выберем координату с

наименьшим номером. Пусть этой компонентой оказалась  .

Дополнительное линейное ограничение запишем в виде:

(2.2)

,

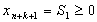(2.3)

6. Добавим условия 2.2. и 2.3 к условиям  -задачи. Получим новую  -задачу. Так как оптимальное решение  -задачи определяло одну из вершин многогранника условий, то оно может быть выбрано в качестве первоначального опорного решения для вновь полученной задачи.

Последнюю симплексную таблицу

-задачи берем в качестве

исходной для

-задачи, дополнив ее условием 2.2.

Симплексная таблица для  -задачи получается из последней путем

окаймления строкой с элементами  ,  ,

j не

принадлежит базису задачи

задачи.

Причем,

,

, j принадлежит базису   задачи.

Получим новую задачу, переменными которой являются  .

Пусть имеет место максимизация целевой функции и решение    -задачи оптимально. Поэтому процесс перехода к новому решению  -задачи от псевдорешения   осуществляется преобразованиями с пересчетом симплекс-таблицы.

Обозначим через k номер псевдорешения  -задачи; тогда направляющей строкой является i+k+1-я строка, k=0,1,2,... Поэтому на каждом этапе преобразования таблицы вектор   будет выводиться из таблицы.

Если решение   задачи завершается построением оптимального целочисленного решения  , то первые m компонент определяют решение целочисленной задачи; если среди координат   решения есть дробные, то одна из дробных компонент порождает дополнительное ограничение и процесс решения должен быть продолжен с новой окаймляющей строкой. Строка, используемая ранее для окаймления, вычеркивается и больше для построения расширенных задач не восстанавливается.

Процедуру решения  -задачи и анализа полученного решения назовем большой итерацией. Номер большой итерации совпадает с номером

решаемой

задачи.

Теорема 2.3.(о конечности первого алгоритма Гомори)

Пусть множество оптимальных планов  -

задачи ограничено

и выполняются следующие условия:

1)   - целые коэффициенты целевой функции F, строка целевой функции в симплексной таблице учитывается при выборе строки для построения правильного отсечения;