Теорема Ролля.

Если функция   непрерывна на  , дифференцируема на   и  , то существует точка  , такая, что  .

Д о к а з а т е л ь с т в о. Если   постоянна на  , то для всех   производная  .

Будем теперь считать, что   непостоянна на  . Так как   непрерывна на  , то существует точка  , в которой   достигает максимума на   (см. § 3.5, теорема 2), и существует точка  , в которой   достигает минимума на  . Обе точки не могут быть концевыми точками отрезка  ,  потому что иначе

и   была бы постоянной на  . Следовательно, одна из точек  ,   принадлежит  к интервалу  . Обозначим ее через  . В ней достигается локальный экстремум. Кроме того,   существует, потому что по условию   существует для всех  . Поэтому по теореме Ферма  .

Теорема Коши

Если функции   и   непрерывны на   и дифференцируемы на  , и   в  , то существует точка   такая, что

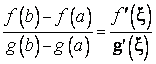.                                                    (4)

Д о к а з а т е л ь с т в о. Отметим, что  , так как в противном случае, по теореме Ролля, нашлась бы точка   такая, что  , чего быть не может по условию теоремы. Составим вспомогательную функцию

.

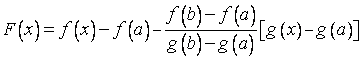В силу условия теоремы эта функция   непрерывна на  , дифференцируема на   и  . Применяя теорему Ролля, получим, что существует точка  , в которой  . Но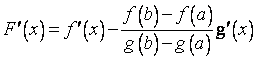 , поэтому, подставляя вместо   точку  , получаем утверждение теоремы.

Теорема Лагранже.

Пусть  функция   непрерывна на отрезке   и имеет производную на интервале  . Тогда существует на интервале   точка  , для которой выполняется равенство

. (5)

Теорема Лагранжа имеет простой геометрический смысл, если записать ее в виде

.

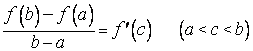Л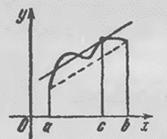 евая часть этого равенства есть тангенс угла наклона к оси хорды, стягивающей точки   и   графика функции  , а правая часть есть тангенс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой  . Теорема Лагранжа утверждает, что если кривая (рис. 51) есть график непрерывной на   функции, имеющей производную на  , то на этой кривой существует точка, соответствующая некоторой абсциссе     такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой   и  . Равенство (5) называется формулой (Лагранжа) конечных приращений. Промежуточное значение   удобно записывать в виде

, где   есть некоторое число, удовлетворяющее неравенствам  . Тогда формула Лагранжа примет вид

. (6). Она верна, очевидно, не только для  , но и для  .

Формула Тейлора

Рассмотрим произвольный многочлен степени 

где  ,  ,  . Пусть   – произвольное число. Разложим многочлен   по степеням  :

Найдем коэффициенты  :

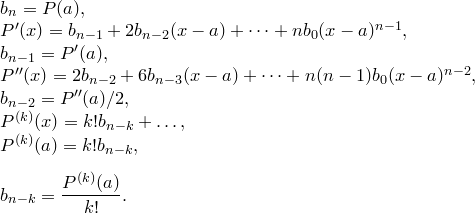
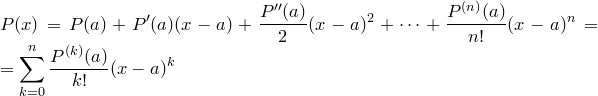
- формула Тейлора для многочленов.

Формула Тейлора 

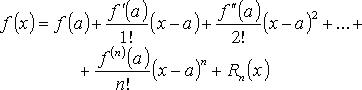
(R_n(x) - остаточный член формулы Тейлора).

     Остаточный член формулы Тейлора 

     В форме Лагранжа:

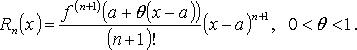
     В форме Коши:

В форме Пеано:

 при 

Основные разложения в ряд Тейлора 

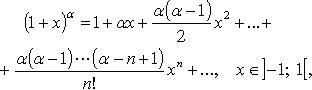
Правило Лопиталя. 

Пусть множество  (a) - проколотая  - окрестность точки a, функции f(x),g(x) определены и дифференцируемы на , g'(x) 0, lim_x af(x) = lim_x ag(x) = 0.

Тогда если существует lim_x af'(x)/g'(x), то существует и предел lim_xaf(x)/g(x), причем справедливо соотношение

lim_x af(x)/g(x) = lim_x af'(x)/g'(x).

Данная теорема без изменений переносится на случай неопределенности вида/.

Замечание. Сформулированная теорема представляет собой лишь достаточное условие. То есть предел отношения функций может существовать и в случае, когда предел отношения производных не существует.

Например, пусть f(x) = x+sin x, g(x) = x-sin x, x. Попробуем применить правило Лопиталя

lim_x(x+sin x)/(x-sin x) = / = =lim_x(x+sin x)'/(x-sin x)' = lim_x (1+cos x)/(1-cos x),

но предел последнего выражения не существует, однако, если поделить числитель и знаменатель на x, то легко получим конечное значения предела:

lim_x(x+sin x)/(x-sin x) = lim_x (1+sin x/x)/(1-sin x/x) = 1

Замечание. Если производные f'(x),g'(x) удовлетворяют тем же требованиям, что и сами функции, то правило Лопиталя можно применить повторно, т.е. предел отношения первых производных можно заменить пределом отношения вторых производных и т.д.

Кроме рассмотренных выше видов неопределенностей вида 0/0 и / часто встречаются неопределенности видов: 0· , 1^, 0^, ⁰. Все эти неопределенности сводятся к двум вида 0/0 и / путем алгебраических преобразований. Продемонстрируем это на примере неопределенностей вида 1^, 0^, ⁰. Каждая из этих неопределенностей имеет вид

y = f(x)g(x),

(9)

где lim_x af(x) = 1;0;, lim_x ag(x) = ;0, Прологарифмировав выражение (9), получим (при f(x)>0 )

ln y = g(x)ln f(x).

Последнее выражение представляет собой при x a неопределенность вида 0·. Покажем, как свести неопределенность вида 0·  к неопределенности вида 0/0 или /.

Пусть y = f(x)g(x), где lim_x af(x) = 0, а lim_x ag(x) = . Но y можно записать иначе, а именно y = f(x)/(1/g(x)), а данное выражение представляет собой при x a неопределенность вида 0/0.