Ф ункция одной переменной

Ф ункция   одной переменной является дифференцируемой в точке   своей области определения  , если существует такая константа  , что для любой точки   верно

при этом число   неизбежно равно производной

Функция одной переменной является дифференцируемой в точке   тогда и только тогда, она имеет производную в этой точке.

График функции   представляет собой кривую на плоскости  , а график линейной функции

доставляет касательную прямую к этой кривой, проведённую в точке  .

Напр., функция   определена и дифференцируема в любой вещественной точке, поскольку её можно представить в виде

.

При этом её производная есть  , а уравнение касательной прямой, проведённой в точке  , имеет вид:  .

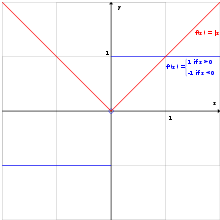
Э лементарные функции могут быть непрерывны в некоторой точке, но не быть в ней дифференцируемы. Напр., функция   является непрерывной на всей вещественной оси, но её производная испытывает скачок при переходе через точку  , в котором эта функция не является дифференцируемой. В этой точке нельзя провести и касательную к графику функции. Функция   тоже непрерывна на всей вещественной оси и её график имеет касательные во всех точках, однако касательная, проведённая в точке  , является вертикальной прямой и поэтому производная функции   бесконечно велика в точке  , а сама функция не дифференцируема в этой точке.

График функции (чёрная кривая) и касательная прямая (красная прямая)

Связь между дифференцируемостью и непрерывностью функции

Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.

Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученный факт или привести пример, который опровергает этот факт.

Найдем производную следующей функции  . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

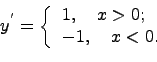
Покажем, что в точке нуль производная не существует. Для этого найдем производную в нуле по определению производной:

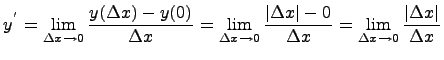
д анный предел равен 1, если   и равен (-1), если  , получаем, что предел не существует, следовательно, в нуле производной нет, и функция в нуле не дифференцируема. 

Геометрический смысл производной.

Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

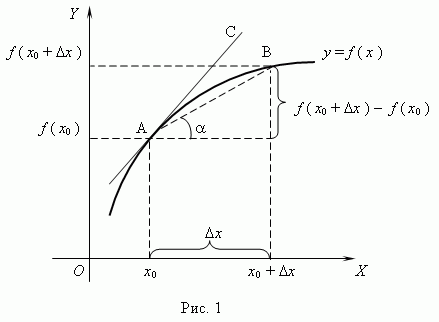
Д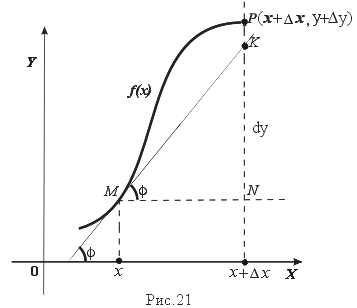 ифференциал.

Дифференциалом функции y = f(x) называется главная линейная относительно D x часть приращения D y, равная произведению производной на приращение независимой переменной dy = f'(x)D x.

Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = D x. Поэтому формулу для дифференциала принято записывать в следующем виде:

dy = f'(x)dx. (4)

Выясним, каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y). Проведем касательную к кривой y = f(x) в точке M, которая образует угол f с положительным направлением оси OX, то есть f'(x) = tg f. Из прямоугольного треугольника MKN, KN = MNtgf = D xtg f = f'(x)D x, то есть dy = KN.

Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение D x. Отметим основные свойства дифференциала, которые аналогичны свойствам производной.

d c = 0;

d(c u(x)) = c d u(x);

d(u(x) ± v(x)) = d u(x) ± d v(x);

d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);

d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v2(x).

Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме (3) равна y' = f'(u)· u'. Тогда дифференциал функции

dy = f'(x)dx = f'(u)u'dx = f'(u)du,

так как u'dx = du. То есть

dy = f'(u)du. (5)

Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.

Замечание. Отметим, что в формуле (4) dx = D x, а в формуле (5) du яляется лишь линейной частью приращения функции u.