Последовательность.

Определение. Последовательностью называется упорядоченное счетное множество чисел .

Обратите внимание, что а) всего чисел - счетное множество и б) они расположены в определенном порядке.

Над последовательностями можно проделывать некоторые операции.

а) Умножение последовательности на число.

Пусть дана последовательность и число c. Тогда произведением последовательности на число c называется последовательность вида .

б) Сложение и вычитание последовательности.

Пусть даны две последовательности и . Суммой и называется последовательность вида

+ = .

Разностью - последовательность видa

- = .

в) Умножение и деление последовательностей.

Произведение последовательностей

= .

Частное последовательностей

.

Определение. Последовательность называется ограниченной сверху, если

ограниченной снизу, если ;

ограниченной, если ;<

(последнее часто пишут так ).

Определение. Говорят, что при n стремящемся к бесконечности, последовательность сходится к пределу a (запись или ) если

Предел последовательности.

Определение (определение предела последовательности). Число A называется пределом x_n, если  > 0  N:  n > N |x_n-A |< .

Предел числовой последовательности обозначается lim_n x_n = A или x_n A при n. Последовательность, имеющая предел, называется сходящейся, в противном случае расходящейся.

Пример. Пусть x_n = 1/n, покажем, что lim_n1/n = 0.

Для этого запишем определение: >0  N:  n>N |x_n|<. То есть 1/n< при n>N=[1/].

Пример.

x_n = .

Доказать, что

lim_{n } = 1

 >0  N:  n > N | -1| < . 1/n <  n > 1/ N = [1/] Если  = 1/10 , то N=10 и при n > 10 следует выполнение нужного неравенства.

В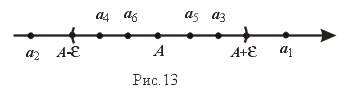 ыясним геометрический смысл понятия предела последовательности. Расположим члены последовательности x₁,x₂,..., x_n,... на числовой прямой. Неравенство |x_n-A|< равносильно следующему A-  < x_n < A + , которое говорит о том, что члены последовательности x_n попадают в  - окрестность точки A (рис.13). Вне этой  -окрестности может быть лишь конечное число членов данной последовательности.

Предел функции и его свойства.

Определение. Число b называется пределом или предельным значением функции при x стремящимся к a (обозначение: , ) если .

Это понятие предела также связано с идеей движения. В этом случае движение отражается в том, что при изменении аргумента x изменяется значение функции. Понятие предела возникает при определенном типе такого движения - когда аргумент приближается к a, то значения функции приближается к b.

а) это значит, что

б) это значит, что

в) это значит, что

г) это значит, что

д) это значит, что

Вариантом этого определения являются так называемые односторонние пределы.

Определение. Число b называется пределом или предельным значением при справа (обозначение ) если

Число b называется пределом или предельным значением при слева (обозначение ) если

Свойства предела функции

Можно показать, что предельное значение функции обладает теми же свойствами, что и пределы последовательности, в частности

1. 

2. 

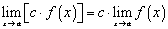
3. eсли

4. Если и , то в некоторой окрестности 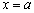ограничена

5. Если , то .

Первый замечательный предел.

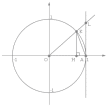
Доказательство

Пусть .

Отложим этот угол на единичной окружности ( ).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке . Точка H — проекция точки K на ось OX.

Очевидно, что: (1)

(где — площадь сектора )

(из : )

Подставляя в (1), получим: ……

Умножаем на :

Перейдём к пределу: ….. …..

Теорема о единственности предела последовательности

Теорема. Любая сходящаяся последовательность имеет единственный предел.

Доказательство. Предположим, что это не так, т. е. xna и xnb одновременно. Выберем числа 1 и 2 таким образом, чтобы множества, задаваемые неравенствами , не пересекались. По определению предела последовательности, начиная с некоторых значений N1 (N2), все члены последовательности принадлежат первому (второму) из этих множеств. Выберем в качестве N3=max(N1, N2). Тогда, начиная с номера N3, все члены последовательности принадлежат обоим этим множествам, что невозможно.

Задание. Доказать, что если последовательность сходится, то она является ограниченной, т. е. все её значения по абсолютной величине не превосходят некоторого числа.

Пример. Доказать, что .

Локальная ограниченность функции, имеющий предел.

Если предел при равняется А, то найдется окрестность , во всех точках которых функция ограниченна.

Док-во:

Положим

Из условия теоремы следует существование окрестности: . Следовательно:

Отсюда для указанных х что и означает ограниченность в .

Предельный переход в неравенствах

Теорема. Пусть - сходящаяся последовательность и . Тогда .

Доказательство этой теоремы проведем методом от противного.

Обозначим . Тогда утверждение, противоположное доказываемому, имеет вид: .

Возьмем . Тогда, по определению, предела последовательности, можно написать

. Последнее неравенство распишем в виде двойного . Но так как , то и получается что , что противоречит условию теоремы.

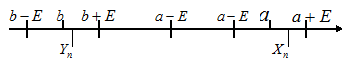
Следствие. Если и сходящиеся последовательности и , то

.

Доказательство дается следующей цепочкой следствий

=> => =>

=>

Таким образом, итог этой теоремы и замечание выглядит так: в неравенствах допустим предельный переход, надо только иметь ввиду, что после предельного перехода строгое неравенство (типа > или <) может замениться на нестрогое

(> перейдет в , < перейдет в ).

Теорема 2. Пусть

1. и сходящиеся последовательности;

2. ;

3. 

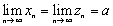
Тогда также сходящаяся последовательность и .

Доказательство: => или

=>

или . Беря и учитывая, что можно записать

. Выбрасывая лишнее, получим что

или ,

что и говорит о том, что .

Эту теорему часто называют “теоремой о двух милиционерах” ( , - милиционеры, - преступник, которого они “берут в клещи”).

О сжатой переменной.

Пусть, начиная с некоторого , выполняются неравенства , причем крайние переменные имеют одинаковый конечный предел , тогда переменная также имеет предел, причем тот же самый.

Доказательство:

Возьмём любое , по определению предела начиная с некоторого номера будут выполняться неравенства:

и

В силу неравенств (*) выполняется неравенство (начиная с некоторого номера ):

Это и означает, что переменная имеет пределом .

Арифметические операции над переменными, имеющими предел.

Пусть существуют пределы: и , тогда существуют пределы переменных:

1.

2.

3.

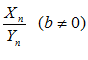
1.

2.

3.

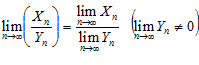
Доказательство:

Доказываем второй случай, остальные доказываются аналогично.

2 случай:

, .

По лемме о бесконечно малых выполняется:

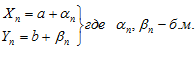
– сумма трех переменных.

Переменная представилась в виде суммы: постоянной и бесконечно малой , это и означает, что постоянная и есть предел этой переменной.

.

Эта теорема представляет другие возможности вычисления предела:

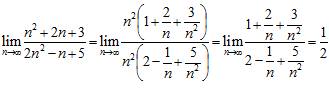
Второй замечательный предел

Числом e называется предел

Это число иррациональное и приближенно равно е = 2.718281828.... Логарифмы с основанием е называются натуральными и обозначаются

Эквивалентные функции

Для того, чтобы функции f(x), g(x) были эквивалентными при x a необходимо и достаточно, чтобы при x a выполнялось хотя бы одно из условий: f(x) = g(x)+o(g(x)) или g(x) = f(x)+o(f(x)).

Заметим, что функции g(x) в первом условии и соответственно функция f(x) во втором называются главной частью функции f(x) (g(x)).

Пример. Функция x – главная часть функции sin x при x 0, так как sin x = x+o(x) при x 0; Если P_n(x) = a_nxⁿ+...+a₁x+a₀, a_n 0, то функция a_nxⁿ является главной частью P_n(x) при x, так как P_n(x) = a_nxⁿ+o(xⁿ) при x.

Функции f(x) и g(x) называются эквивалентными при x a, если (x): f(x) =  (x)g(x), где lim_{x a} (x) = 1.

Иначе говоря функции эквивалентны при x a, если предел их отношения при x a равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами:

sin x ~ x, x  0

(1)

tg x ~ x, x  0,

arcsin x ~ x, x  0,

arctg x~ x, x  0

e^x-1~ x, x 0

ln (1+x)~ x, x 0

(2)

m-1~ mx, x 0

Символ О.

Если для функций f(x), g(x) существуют постоянные c>0, >0, такие, что |f(x)| c |g(x)| при |x-a|<, x a, то говорят, что f является ограниченной по сравнению с функцией g в окрестности точки a и пишут, что f(x) = O(g(x)) при x a.

Данное определение переносится и на случай, когда x, x.

Пример.

1. Так как |1/x²|  |1/x| при |x|  1, то 1/x² = O(1/x) при x ;

2. 1/x = O(1/x²) при x 0 так как |1/x| 1/x² при |x| 1.

Запись f=O(1) при x a означает, что функция f(x) ограничена в некоторой окрестности точки a.

Теорема Больцамо – Вейерштрасса.

Пусть предложена последовательность точек пространства : . И пусть эта последовательность ограничена, то есть , где — некоторое число. Тогда из данной последовательности можно выделить подпоследовательность ,которая сходится к некоторой точке пространства . Доказательство. Докажем, что из любой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность. Нижеизложенный способ доказательства называется методом Больцано, или методом деления пополам. Пусть дана ограниченная числовая последовательность Из ограниченности последовательности следует, что все её члены лежат на некотором отрезке числовой прямой, который обозначим . Разделим отрезок пополам на два равных отрезка. По крайней мере один из получившихся отрезков содержит бесконечное число членов последовательности. Обозначим его . На следующем шаге повторим процедуру с отрезком : разделим его на два равных отрезка и выберем из них тот, на котором лежит бесконечное число членов последовательности. Обозначим его . Продолжая процесс получим последовательность вложенных отрезков , в которой каждый последующий является половиной предыдущего, и содержит бесконечное число членов последовательности . Длины отрезков стремятся к нулю: В силу принципа вложенных отрезков Коши — Кантора, существует единственная точка , принадлежащая всем отрезкам: По построению на каждом отрезке лежит бесконечное число членов последовательности. Выберем последовательность соблюдая при этом условие возрастания номеров: Тогда подпоследовательность сходится к точке . Это следует из того, что расстояние от до не превосходит длины содержащего их отрезка , откуда .