Доказательство
То, что отрезок [0,1] есть бесконечное множество – очевидно.
Предположим противное, т.е. то, что отрезок [0,1] есть счетное множество. Тогда все его точки
можно
представить в форме последовательности
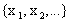,обратите
внимание на слова “все его точки”.
П
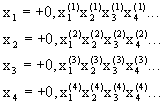оставим
каждой точке в соответствие вещественное
число, согласно описанной выше процедуре.
Ясно, что все эти числа будут иметь знак
+ и их цифра перед запятой будет равна
0. Обратите внимание на индексацию цифр.
Чему соответствует верхний индекс и
что определяет нижний индекс?
1)
Построим число
.
по следующему правилу:
а) его знак +, перед запятой стоит 0
б)
первая цифра после запятой – любая,
кроме
.
в)
вторая цифра после запятой – любая,
кроме
.
…………………………………
г)
вообще, n-ая цифра после запятой – любая,
кроме
.
Обратите
внимание, что при построении
снова
был использован прием диагонализации.
Требование
связано
с запретом на числа вида
Что же хорошего можно сказать о точке, соответствующей числу ?
а)
во-первых ясно, что
:
об этом говорит то, что перед запятой
стоит комбинация +0.
б)
но, с другой стороны,
;
;
… Вообще, для любого n
.Поэтому
.
Вот
тут и кроется противоречие. Ведь в п.1
предполагалось, что в последовательности
перебраны
все
точки интервала[0,1]. И вдруг оказалась
еще одна точка из этого же интервала,
которой нет в этой последовательности.
Получившееся противоречие доказывает
нашу теорему.
Определение. Множества, эквивалентные по числу элементов отрезку [0,1] называются множествами мощности континуума .
Теорема. Отрезки (а,в),(а,в],[а,в) также имеют мощность континуума .
Доказательство
Формула
y=a+x(b-a) устанавливает взаимно-однозначное
соответствие между
.
Рассмотрим отрезок (a,b). Отрезок [a,b] получается из (a,b) добавлением всего лишь двух точек: а и b. Как мы уже знаем, от добавления к бесконечному множеству конечного числа элементов его мощность не меняется. Поэтому отрезки (a,b) и [a,b] имеют одинаковую мощность, а т.к. [a,b] имеет мощность континуума, то и (а,b) имеет мощность континуума.
Покажите
сами, что вся прямая
имеет
мощность континуума (установив, например,
взаимно-однозначное соответствие
отрезков (-1,1) и
,
)
.
Следствие Множество вещественных чисел имеет мощность континуума.
Вспомним, что счетное множество – самое “маленькое” из всех бесконечных множеств. Поэтому можно сказать, что вещественных чисел гораздо больше, чем рациональных – ведь вещественных чисел континуум, а рациональных – всего лишь счетное множество.
Аксиоматика действительных чисел.
Пространство действительных чисел. Множество R называется пространством действительных чисел, а его элементы – действительными числами, если выполнены следующие аксиомы:
Аксиома сложения (x, y) R R z = x+y R, называемый суммой x и y . (Cимвол означает квантор существования и читается "существует".) При этом выполнены следующие свойства:
нейтральный элемент 0, называемый нулем, такой, что для любого x R, x+0=0+x = x
Для любого элемента x R существует элемент -x R , называемый противоположным к x, такой, что x+(-x) = (-x)+x = 0
Операция сложения ассоциативна, т.е. для любых x,y,z R выполнено условие, (x+y)+z = x+(y+z)
Операция сложения коммутативна, т.е. для любых x,y R, y+x = x+y
Аксиома умножения. (x,y) R R ставится в соответствие элемент z = x· y R, называемый произведением, при этом выполнены следующие условия
Существует нейтральный элемент 1 R\ 0 называемый единицей, такой, что x R, x· 1=1· x = x.
Для любого элемента x R\ 0 найдется элемент x-1 R \ 0, называемый обратным, такой, что, x· x-1 = x-1· x = 1.
Операция умножения ассоциативна, т.е. x,y,z R\ 0, x· (y· z) = (x· y)· z.
Операция умножения коммутативна, т.е. для любых x,y R\ 0, x· y = y· x.
Аксиома порядка. Между элементами множества R имеется отношение , т.е. для элементов x,y R установлено x y или нет. При этом выполняются следующие условия:
x x
x y и y x y = x
x y и y z x z
x,y R x y или y x.
Связь порядка и сложения. Если x,y,z R, то из x y следует, что x+z y+z
Связь порядка и умножения. Если x 0, y 0, то x · y 0
Аксиома непрерывности. Если X,Y R-непустые,и при x X и y Y, выполнено условие x y, то c R: x c y.