Т очка перегиба.

Точка перегиба. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция имеет разные направления выпуклости.

Нетрудно заметить, что точки перегиба - это точки экстремума первой производной. Отсюда следуют утверждения.

Необходимое условие перегиба. Вторая производная f''(x) дважды непрерывно дифференцируемой функции в точке перегиба x0 равна нулю, т.е. f''(x0) = 0.

Достаточное условие перегиба. Если вторая производная дважды дифференцируемой функции при переходе через точку x0, в которой f''(x0) = 0 меняет свой знак, то x0 есть точка перегиба ее графика.

Заметим, что если в окрестности точки x₁ функция выпукла вниз, то график функции находится выше касательной, а если в окрестности точки x₂ функция выпукла вверх, то график функции находится ниже касательной. В точке перегиба x₀ касательная разделяет график - он лежит по разные стороны касательной. (рис. 27).

Рассмотрим пример, иллюстрирующий исследование функции на выпуклость и точки перегиба.

Пример. Найти интервалы выпуклости и точки перегиба функции y = x⁴+x³-18x²+24x -12.

Решение. Находим производные y' = 4x3+3x2-36x+24, y'' = 12x2+6x-36.

Отсюда y'' = 0 при x₁ = -2, x₂ = 3/2. Следовательно, y''>0 на интервалах (-,-2), (3/2,) и функция выпукла вниз; y''<0 на интервале (-2,3/2) и функция выпукла вверх на этом интервале. Так как при переходе через точки x₁ = -2 и x₂ = 3/2 вторая производная меняет знак, то точки (-2,-124) и (3/2,-129/16) являются точками перегиба.

А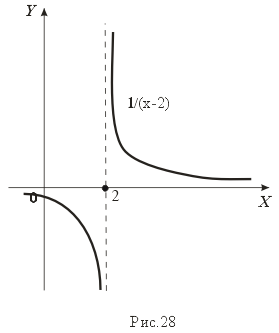 симптоты графика функции.

Вертикальная асимптота. Прямая x = a называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из пределов

lim_x a+0f(x) или lim_x a-0f(x)

равен + или -.

Пример 14. График функции y = 1/(x-2) имеет вертикальную асимптоту x = 2, так как lim_x 2+01/(x-2) = +, lim_x 2-01/(x-2) = - (рис.28).

Наклонная асимптота. Говорят, что прямая y = kx+b является наклонной асимптотой графика функции y = f(x) при x, если f(x) имеет вид

f(x) = kx+b+ (x),

где lim_{x} (x) = 0.

Справедлива

Теорема (существование асимптот). 

Для того чтобы график функции y = f(x) имел при x асимптоту y = kx+b, необходимо и достаточно, чтобы существовали два предела

lim_xf(x)/x = k, lim_x(f(x)-kx) = b.

Доказательство.

1. Необходимость. Пусть график функции y = f(x) имеет при x асимптоту y = kx+b, то есть для f(x) имеет вид

f(x) = kx+b+(x),

тогда

lim_xf(x)/x = (kx+b+(x))/x = k,

lim_x(f(x)-kx) = lim_x(b+(x)) = b.

2. Достаточность. Пусть существуют пределы, фигурирующие в условии теоремы. Тогда величина f(x)-kx-b является бесконечно малой при x. Обозначив f(x)-kx-b = (x) получим, что f(x) имеет асимптоту согласно определению наклонной асимптоты.

Замечание. Аналогично определяется наклонная асимптота и доказывается теорема 13 при x.

Замечание. Если k=0 в определении наклонной асимптоты, то наклонная асимптота является горизонтальной.

Пример. Найти асимптоты кривой: y = 5x/(x-3).

Решение. Кривая имеет вертикальную асимптоту x = 3, так как

lim_x 3 05x/(x-3) = .

Найдем наклонную асимптоту:

k = lim_xy/x = lim_x5x/x(x-3) = 0. b = lim_x(y-kx) =lim_x5x/(x-3) = 5.

Итак, данная кривая имеет вертикальную асимптоту x = 3 и горизонтальную асимптоту y = 5.