Необходимое условие экстремума.

М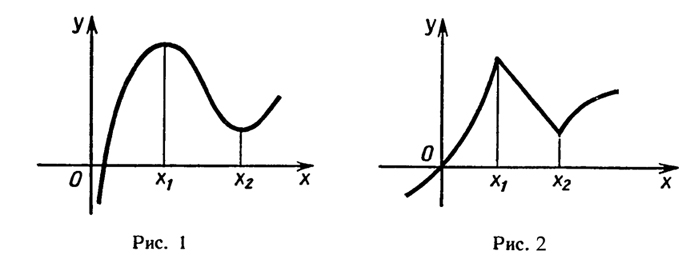 ы рассмотрели поведение функции на промежутках, где f(х)>0 и f'(х)<0. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции (рис. 1 и 2). Сформулируем соответствующее утверждение, его называют теоремой Ферма (в честь французского математика Пьера Ферма).

Необходимое условие экстремума. Если точка хо является точкой экстремума функции f и в этой точке существует производная f’, то она равна нулю:F’(x₀) =0. Рассмотрим случай f'(x₀)>0. По определению производной отношение   при х→х0 стремится к положительному числу f' (х₀), а следовательно, и само будет положительно при всех х, достаточно близких к x₀. Для таких х

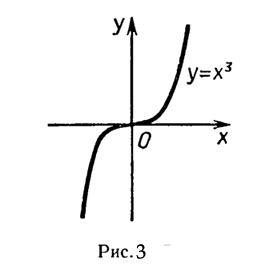
и, значит, f(x)>f(x₀) для всех х>х₀ из некоторой окрестности точки x₀. Поэтому х₀ не является точкой максимума. Если же х<х₀, то f (x)<f(x₀), и, следовательно, х₀ не может быть и точкой минимума f. Случай F'(x₀)<0 разбирается аналогично. Важно отметить, что теорема Ферма есть лишь необходимое условие экстремума: из того, что производная в точке хо обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум. Например, производная функции f(х)=х³ обращается в нуль в точке 0, но экстремума в этой точке функция не имеет.

Достаточное условие локального экстремума.

Пусть точка x0- стационарная точка функции f. Если f дифференцируема в некоторой окрестности U(x0) точке x0, а в самой точке x0 она дважды дифференцируема и f′′(x0)/=0 , то f(x0) -- есть локальный экстремум функции f, а именно f(x0)является локальным max, если f′′(x0)<0и f(x0) -- локальным min, если f′′(x0)>0. Доказательство: Пусть f′′(x0)<0, тогда функция f′ в точке x0 будет убывающей, т.е. для точек x левой полуокрестности U−(x0) точки x0будет иметь f′(x)>f′(x0)=0, для точки x∈U+(x0),f′(x)<f′(x0)=0 , т.е. при переxоде через точку x0производная f′ меняет свой знак с `+' на `-'. По теореме 2 получаем, чтоf(x0)является локальным max функции f. 2) Пусть f′′(x0)>0, тогда функция f′ в точке x0 будет возрастающей. Поскольку x0- стационарная точка функции, т.е.f′(x0)=0, то это означает, что при переxоде через точку x0 производная f′ меняет свой знак с `-' на `+', что и означает, чтоf(x0) локальный min функции f. ч.т.д. Определение Точка М(x0,f(x0)) называется точкой перегиба графика функции f(x), если в точке М график имеет касательную и существует такая окрестность точки x0, в пределаx которой график функции слева и справа от точки x0 имеет разные направления выпуклости.

В ыпуклость функции.

Определение. Множество точек на плоскости называется выпуклым, если отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве.

Примерами выпуклых множеств являются: треугольник, отрезок, полуплоскость, вся плоскость.

Определение. Функция y = f(x) называется выпуклой вниз (вверх) на множестве X, если для всех x₁,x₂ X выполняется неравенство

f(₁ x1+₂x2)₁f(x1)+ ₂f(x2) (f(₁ x1+₂x2)₁f(x1)+ ₂f(x2)),

где ₁ 0,₂ 0, ₁+₂ = 1.

Графики функций, выпуклых вниз и вверх, изображены на рис. 25.

С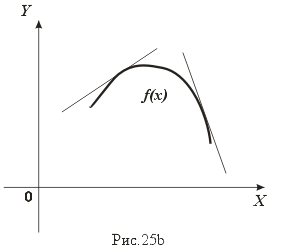 праведлива

Теорема. Функция выпукла вниз (вверх) на множестве X тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).

Геометрический смысл теоремы состоит в том, что если f'(x) возрастает (убывает) на множестве X, то возрастает (убывает) угол наклона касательных к графику (рис.26). Это и означает выпуклость функции вниз (вверх).

Приведем достаточное условие выпуклости функции вниз (вверх).

Д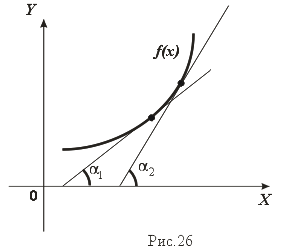 остаточное условие выпуклости. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) на множестве X, то функция выпукла вниз (вверх) на этом множестве.

Доказательство. Если f''(x)>0, x X, то f'(x) возрастает на множестве X и по предыдущей теореме функция выпукла вниз на множестве X. Аналогично рассматривается случай, когда f''(x)<0.

Необходимое условие выпуклости слабее: если функция выпукла вниз (вверх) на множестве X, то f''(x) 0, x X (или f''(x) 0 ) x X. Например, функция y = x⁴выпукла вниз на всей числовой прямой, но y'' = 12x² обращается в ноль при x = 0.