Програмки с отчётами по числакам / 3. Краевая задача для ОДУ 2 порядка / 3. Вар 3
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ
Отчет по лабораторной работе № 3
«ЧИСЛЕННОЕ РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ»
|
Программа/ Результат |
Теоретический материал |
Оценка |
|
|
|
|
Группа: Ф-03
Курс: Численные методы
Выполнил:
Преподаватель: Рябов Павел Николаевич
Москва 2012 год
-
Полная постановка задачи:
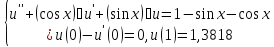
-
График точного решения
 :
:

-
Результаты, полученные при выполнении лабораторной работы:
Для шага h=0.05
|
Точное
решение задачи,
|
Численное
решение задачи с аппроксимацией
краевых условий с первым порядком
точности,
|
Численное решение задачи с аппроксимацией краевых условий со вторым порядком точности,
|
|
1,00000000 1,04872943 1,09483758 1,13820921 1,17873591 1,21631638 1,25085670 1,28227052 1,31047934 1,33541264 1,35700810 1,37521175 1,38997809 1,40127020 1,40905987 1,41332763 1,41406280 1,41126355 1,40493688 1,39509859 1,38177329 |
0.989512 1.038988 1.085808 1.129859 1.171035 1.209239 1.244377 1.276365 1.305127 1.330593 1.352703 1.371404 1.386651 1.398409 1.406649 1.411354 1.412513 1.410126 1.404199 1.3947486 1.3818000 |
0,99985708 1.04860011 1.09472165 1.13810639 1.17864587 1.21623874 1.25079100 1.28221627 1.31043597 1.33537953 1.35698459 1.37519711 1.38997156 1.40127098 1.40906710 1.41334043 1.41408026 1.41128475 1.40496087 1.39512443 1.38180000
|
|
Модуль
разности точного решения и численного
в первом случае,
|
Модуль
разности точного решения и численного
во втором случае,
|
|
1.05e-002 9.74e-003 9.03e-003 8.35e-003 7.70e-003 7.08e-003 6.48e-003 5.91e-003 5.35e-003 4.82e-003 4.30e-003 3.81e-003 3.33e-003 2.86e-003 2.41e-003 1.97e-003 1.55e-003 1.14e-003 7.38e-004 3.50e-004 2.67e-005 |
1.43e-004 1.29e-004 1.16e-004 1.03e-004 9.00e-005 7.76e-005 6.57e-005 5.42e-005 4.34e-005 3.31e-005 2.35e-005 1.46e-005 6.53e-006 7.71e-007 7.22e-006 1.28e-005 1.75e-005 2.12e-005 2.40e-005 2.58e-005 2.67e-005 |
Для шага h=0.1 приведена только вторая таблица.
|
Модуль
разности точного решения и численного
в первом случае,
|
Модуль
разности точного решения и численного
во втором случае,
|
||||||||||||||||||||||
|
|
Код с 1 порядком аппроксимации
#include<stdio.h>
#include<math.h>
#include<conio.h>
double h= 0.05 , lbnd= 0.0, rbnd= 1.0; //шаг и границы отрезка
const int n = 20; // равно (rbnd-lbnd)/h
double p(double x) {
return cos(x) ;
}
double q(double x) {
return sin(x) ;
}
double f(double x) {
return 1-cos(x)-sin(x) ;
}
double u0(double x) {
return sin(x)+cos(x) ;
}
void Progon (double *a, double *b, double *c, double *d, double *y)
{
double A[n], B[n], C[n], D[n] ; //прогоночные коэффициенты
// Прямой ход
A[0]= -c[0]/b[0] ; B[0]= d[0]/b[0] ;
for (int i=1; i< n; i++) {
A[i]= -c[i]/(b[i] + a[i]*A[i-1]) ;
B[i]= (d[i] - a[i]*B[i-1])/(b[i] + a[i]*A[i-1]) ;
}
// Обратный ход
y[n]= (d[n]-a[n]*B[n-1]) / (b[n]+a[n]*A[n-1]) ;
for (int i= n-1; i>= 0; i--) {
y[i]= A[i]*y[i+1] + B[i] ;
}
}
int main()
{
double xi, y[n], a[n], b[n], c[n], d[n] ;
/* double *a = (double*)malloc(n*sizeof(double)); */
//Производная во внутренних точках аппроксимирована со 2 порядком точности (не менять)
xi= lbnd + h ;
for (int i= 1; i< n; i++) {
a[i]= 1/h/h - p(xi)/2/h ;
b[i]= q(xi) - 2/h/h ;
c[i]= 1/h/h + p(xi)/2/h ;
d[i]= f(xi) ;
xi += h ;
}
//Коэффициенты для левой границы аппроксимированы с 1ой точностью, a[0]=0:
a[0]= 0; b[0]=(1+h) ;
c[0]= -1; d[0]= 0 ;
//Коэффициенты для правой границы аппроксимированы с 1ой точностью, c[n]=0:
a[n]= 0; b[n]= 1 ;
c[n]= 0; d[n]= 1.3818 ;
Progon(a, b, c, d, y) ; //в массиве y окажутся численные значения решения
FILE *file;
file = fopen("c:/3-1order.txt", "w");
printf(" x u0 (x) y(x) |y-u0| \n\n") ;
fprintf(file, " x u0 (x) y(x) |y-u0| \n\n") ;
xi= lbnd;
for (int i= 0; i<= n; i++) {
printf("%.3f %.10f %.10f %.2e\n", xi, u0(xi), y[i], abs(y[i]-u0(xi)) ) ;
fprintf(file, "%.3f %.10f %.10f %.2e\n", xi, u0(xi), y[i], abs(y[i]-u0(xi)) ) ;
xi += h ;
}
getch();
return 0;
}
Код со 2 порядком аппроксимации
#include<stdio.h>
#include<math.h>
#include<conio.h>
double h= 0.05 , lbnd= 0.0, rbnd= 1.0; //шаг и границы отрезка
const int n = 20; // равно (rbnd-lbnd)/h
double p(double x) {
return cos(x) ;
}
double q(double x) {
return sin(x) ;
}
double f(double x) {
return 1-cos(x)-sin(x) ;
}
double u0(double x) {
return sin(x)+cos(x) ;
}
void Progon (double *a, double *b, double *c, double *d, double *y)
{
double A[n], B[n], C[n], D[n] ; //прогоночные коэффициенты
// Прямой ход
A[0]= -c[0]/b[0] ; B[0]= d[0]/b[0] ;
for (int i=1; i< n; i++) {
A[i]= -c[i]/(b[i] + a[i]*A[i-1]) ;
B[i]= (d[i] - a[i]*B[i-1])/(b[i] + a[i]*A[i-1]) ;
}
// Обратный ход
y[n]= (d[n]-a[n]*B[n-1]) / (b[n]+a[n]*A[n-1]) ;
for (int i= n-1; i>= 0; i--) {
y[i]= A[i]*y[i+1] + B[i] ;
}
}
int main()
{
double xi, y[n], a[n], b[n], c[n], d[n] ;
/* double *a = (double*)malloc(n*sizeof(double)); */
//Производная во внутренних точках аппроксимирована со 2 порядком точности (не менять)
xi= lbnd + h ;
for (int i= 1; i< n; i++) {
a[i]= 1/h/h - p(xi)/2/h ;
b[i]= q(xi) - 2/h/h ;
c[i]= 1/h/h + p(xi)/2/h ;
d[i]= f(xi) ;
xi += h ;
}
//Коэффициенты для левой границы аппроксимированы с 2ой точностью, a[0]=0:
a[0]=0; b[0]=(2*h-h*h+2) ;
c[0]= -2; d[0]= 0 ;
//Коэффициенты для правой границы аппроксимированы с 2ой точностью, c[n]=0:
a[n]= 0; b[n]= 1 ;
c[n]= 0; d[n]= 1.3818 ;
Progon(a, b, c, d, y); //в массиве y окажутся численные значения решения
FILE *file;
file = fopen("c:/3-2order.txt", "w");
xi= lbnd;
printf(" x u0 (x) y(x) |y-u0| \n\n") ;
fprintf(file, " x u0 (x) y(x) |y-u0| \n\n") ;
for (int i= 0; i<= n; i++) {
printf("%.3f %.10f %.10f %.2e\n", xi, u0(xi), y[i], abs(y[i]-u0(xi)) ) ;
fprintf(file, "%.3f %.10f %.10f %.2e\n", xi, u0(xi), y[i], abs(y[i]-u0(xi)) ) ;
xi += h ;
}
getch();
return 0;
}